相似三角形的判定教案/学案[下学期]
文档属性
| 名称 | 相似三角形的判定教案/学案[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 61.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-01-10 12:38:00 | ||
图片预览



文档简介
相似三角形的判定
一. 本周教学内容:
相似三角形的判定
二. 重点、难点
重点:掌握相似三角形的判定方法。
难点:灵活运用相似三角形的判定方法解决有关问题。
三. 教学过程
(一)复习
1. 相似三角形的定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2. 注意:
(1)定义中对应角相等,对应边成比例,是指3组对应角分别相等,三组对应边成比例。
(2)读作相似于,与全等三角形一样,表示对应顶点的字母应写在对应位置上。
(3)所谓相似三角形是指两个三角形形状一样,大小不一定一样。
(4)相似三角形定义本身揭示了相似三角形的性质:相似三角形对应角相等,对应边成比例。
(5)相似比带有顺序性,如的相似比为
反过来的相似比为
(6)全等三角形是相似比为1的相似三角形,但相似三角形不一定是全等三角形。
(二)三角形相似的判定方法
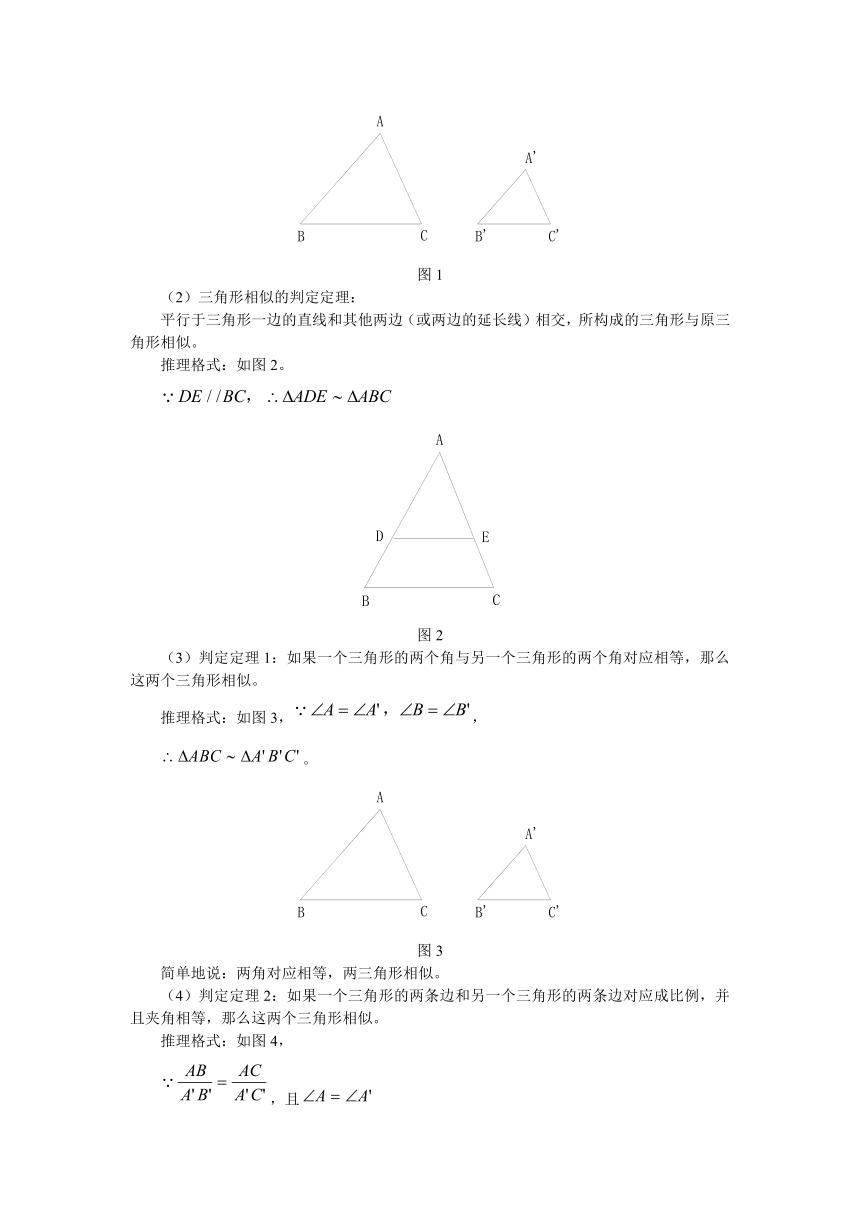
(1)定义法:对应角相等,对应边成比例的三角形相似。
如图1,若,,
则。
与三个角对应相等,三条边对应相等,两个三角形全等类似,定义法在计算和证明中一般用得较少。
图1
(2)三角形相似的判定定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
推理格式:如图2。
图2
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
推理格式:如图3,,
。
图3
简单地说:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
推理格式:如图4,
,且
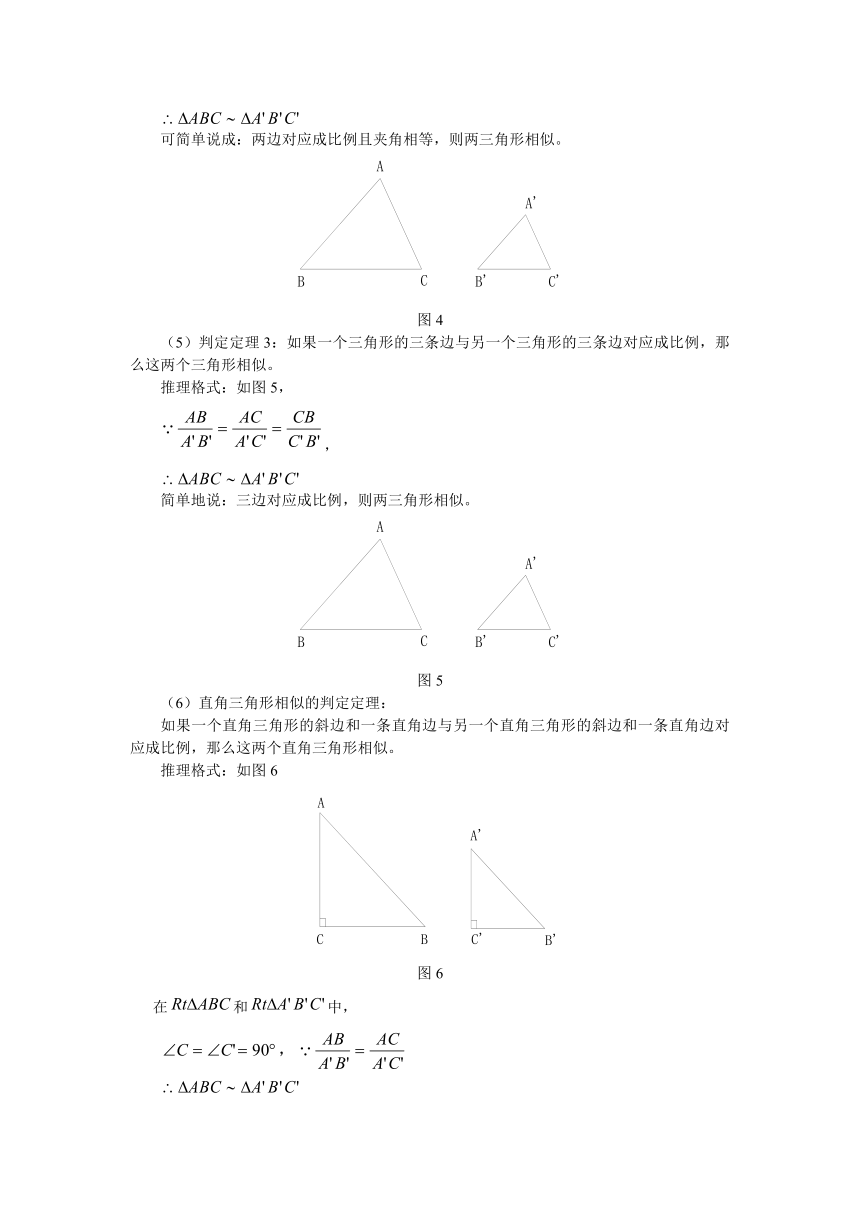
可简单说成:两边对应成比例且夹角相等,则两三角形相似。
图4
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
推理格式:如图5,
,
简单地说:三边对应成比例,则两三角形相似。
图5
(6)直角三角形相似的判定定理:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
推理格式:如图6
图6
在和中,
推论:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似(如图7)。
图7
说明:灵活运用相似三角形的判定方法解决相关问题,其关键是确定相似三角形,通常按下列思路来分析:
1. 有平行线(有时要构造平行线)时,可选择平行法判定三角形相似。
2. 若已经有一组角相等,可再找另一组角相等,运用判定定理1;或再证明夹这组角的两边对应成比例,运用判定定理2。
3. 若已知两条对应边成比例,可找夹角相等,运用判定定理2。
4. 若是两个直角三角形,可找一对锐角相等或夹直角的两直角边对应成比例,或应用斜边、直角边对应成比例来判定相似。
5. 利用相似三角形的传递性证相似,如:若、,则。
6. 注意:仅两边成比例,一对角相等的三角形不一定相似。
【典型例题】
例1. 如图8,四边形ABCD的对角线相交于点O,。求证:。
图8
分析:欲证,可寻求它们所在的三角形与相似,
而,故只需证,
由已知可得,从而有成立。
证明:
说明:由于相似三角形的对应角相等,所以经常运用此法证明角的相等。
例2. 如图9,平行四边形ABCD中,E是AB延长线上一点,连结DE,交AC于G,交BC于F,那么图中相似三角形(不含全等三角形)共有( )对。
A. 6 B. 5 C. 4 D. 3
图9
分析:找相似形一找平行线、二找角相等、三找线段成比例,本题只能从前两方面入手。
解:
共有5对,选B。
例3. 已知:如图10,,,
(1)当BD与a、b之间满足怎样的关系时,?
(2)当BD与a、b之间满足怎样的关系时,?
(3)当BD与a,b之间满足怎样的关系时,这两个三角形相似?
图10
解:(1)
当时,
即时,
故当时,
(2),
当时,
即时,
当时,
(3)综合(1),(2)可知:
当或时这两个三角形相似。
【模拟试题】(答题时间:20分钟)
一. 选择题:
1. 在直角三角形中,两直角边分别为3、4,则这个三角形的斜边与斜边上的高的比是( )
A. B. C. D.
2. 中,D是AB上的一点,在AC上取一点E,使得以A、D、E为顶点的三角形与相似,则这样的点的个数最多是( )
A. 0 B. 1 C. 2 D. 无数
3. 如图1,正方形ABCD中,E是CD的中点,,下面得出六个结论:(1);(2);(3);(4);(5);(6)。其中正确的个数是( )
A. 1个 B. 3个 C. 4个 D. 5个
图1
4. (哈尔滨市,2002)已知,如图2,中,P为AB上一点,在下列四个条件中:(1);(2);(3);(4)。能满足和相似的条件是( )
A. (1)(2)(4) B. (1)(3)(4)
C. (2)(3)(4) D. (1)(2)(3)
图2
5. 如图3,正方形ABCD的对角线AC、BD相交于点O,E是BC的中点,DE交AC于F,若,则EF等于( )
A. 8 B. 6 C. 4 D. 3
图3
二. 解答题:
1. 已知:中,于D,E为AC中点,ED的延长线交AB的延长线于F。求证:(1);(2)。
2. 如图4,中,于D,E是CD的中点,AE的延长线交BC于F,,垂足为H,若,求FH。
图4
3. 如图5,N为的边BC上一点,,D为AC的中点,并且AN交BD于E。求证:。
图5
4. 在中,,延长BC至E,使,D为EC中点。求证:。
【试题答案】
一. 1. A(可求斜边长为5,斜边上的高为)
2. C(可作或)
3. B(设CD=4,则
,从而得
又
,由传递性。
故(4)、(5)、(6)正确。)
4. D
5. C(连结OE,则OE//CD且
由得)
二. 1. (1)E为AC中点,
,故
又
故
而,
(2)易得
2. 延长AC、HF交于G。
先证,可得
由E为CD的中点得,
3. 有中点时通常作平行线。
过点N作NM//BD交AC于M。
,
又
,在中,ED//NM,
,
4.
又
又
【励志故事】
把失败写在背面(一)
有一个年轻人,从很小的时候起,他就有一个梦想,希望自己能够成为一名出色的赛车手。他在军队服役的时候,曾开过卡车,这对他熟练驾驶技术起到了很大的帮助作用。
退役之后,他选择到一家农场里开车。在工作之余,他仍一直坚持参加一支业余赛车队的技能训练。只要有机会遇到车赛,他都会想尽一切办法参加。因为得不到好的名次,所以他在赛车上的收入几乎为零,这也使得他欠下一笔数目不小的债务。
那一年,他参加了威斯康星州的赛车比赛。当赛程进行到一半多的时候,他的赛车位列第三,他有很大的希望在这次比赛中获得好的名次。
突然,他前面那两辆赛车发生了相撞事故,他迅速地转动赛车的方向盘,试图避开他们。但终究因为车速太快未能成功。结果,他撞到车道旁的墙壁上,赛车在燃烧中停了下来。
当他被救出来时,手已经被烧伤,鼻子也不见了。体表伤面积达40%。医生给他做了7个小时的手术之后,才使他从死神的手中挣脱出来。
经历这次事故,尽管他命保住了,可他的手萎缩得像鸡爪一样。医生告诉他说:“以后,你再也不能开车了。”
(未完,下期待续)
一. 本周教学内容:
相似三角形的判定
二. 重点、难点
重点:掌握相似三角形的判定方法。
难点:灵活运用相似三角形的判定方法解决有关问题。
三. 教学过程
(一)复习
1. 相似三角形的定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2. 注意:
(1)定义中对应角相等,对应边成比例,是指3组对应角分别相等,三组对应边成比例。
(2)读作相似于,与全等三角形一样,表示对应顶点的字母应写在对应位置上。
(3)所谓相似三角形是指两个三角形形状一样,大小不一定一样。
(4)相似三角形定义本身揭示了相似三角形的性质:相似三角形对应角相等,对应边成比例。
(5)相似比带有顺序性,如的相似比为
反过来的相似比为
(6)全等三角形是相似比为1的相似三角形,但相似三角形不一定是全等三角形。
(二)三角形相似的判定方法
(1)定义法:对应角相等,对应边成比例的三角形相似。
如图1,若,,
则。
与三个角对应相等,三条边对应相等,两个三角形全等类似,定义法在计算和证明中一般用得较少。
图1
(2)三角形相似的判定定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
推理格式:如图2。
图2
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
推理格式:如图3,,
。
图3
简单地说:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
推理格式:如图4,
,且
可简单说成:两边对应成比例且夹角相等,则两三角形相似。
图4
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
推理格式:如图5,
,
简单地说:三边对应成比例,则两三角形相似。
图5
(6)直角三角形相似的判定定理:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
推理格式:如图6
图6
在和中,
推论:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似(如图7)。
图7
说明:灵活运用相似三角形的判定方法解决相关问题,其关键是确定相似三角形,通常按下列思路来分析:
1. 有平行线(有时要构造平行线)时,可选择平行法判定三角形相似。
2. 若已经有一组角相等,可再找另一组角相等,运用判定定理1;或再证明夹这组角的两边对应成比例,运用判定定理2。
3. 若已知两条对应边成比例,可找夹角相等,运用判定定理2。
4. 若是两个直角三角形,可找一对锐角相等或夹直角的两直角边对应成比例,或应用斜边、直角边对应成比例来判定相似。
5. 利用相似三角形的传递性证相似,如:若、,则。
6. 注意:仅两边成比例,一对角相等的三角形不一定相似。
【典型例题】
例1. 如图8,四边形ABCD的对角线相交于点O,。求证:。
图8
分析:欲证,可寻求它们所在的三角形与相似,
而,故只需证,
由已知可得,从而有成立。
证明:
说明:由于相似三角形的对应角相等,所以经常运用此法证明角的相等。
例2. 如图9,平行四边形ABCD中,E是AB延长线上一点,连结DE,交AC于G,交BC于F,那么图中相似三角形(不含全等三角形)共有( )对。
A. 6 B. 5 C. 4 D. 3
图9
分析:找相似形一找平行线、二找角相等、三找线段成比例,本题只能从前两方面入手。
解:
共有5对,选B。
例3. 已知:如图10,,,
(1)当BD与a、b之间满足怎样的关系时,?
(2)当BD与a、b之间满足怎样的关系时,?
(3)当BD与a,b之间满足怎样的关系时,这两个三角形相似?
图10
解:(1)
当时,
即时,
故当时,
(2),
当时,
即时,
当时,
(3)综合(1),(2)可知:
当或时这两个三角形相似。
【模拟试题】(答题时间:20分钟)
一. 选择题:
1. 在直角三角形中,两直角边分别为3、4,则这个三角形的斜边与斜边上的高的比是( )
A. B. C. D.
2. 中,D是AB上的一点,在AC上取一点E,使得以A、D、E为顶点的三角形与相似,则这样的点的个数最多是( )
A. 0 B. 1 C. 2 D. 无数
3. 如图1,正方形ABCD中,E是CD的中点,,下面得出六个结论:(1);(2);(3);(4);(5);(6)。其中正确的个数是( )
A. 1个 B. 3个 C. 4个 D. 5个
图1
4. (哈尔滨市,2002)已知,如图2,中,P为AB上一点,在下列四个条件中:(1);(2);(3);(4)。能满足和相似的条件是( )
A. (1)(2)(4) B. (1)(3)(4)
C. (2)(3)(4) D. (1)(2)(3)
图2
5. 如图3,正方形ABCD的对角线AC、BD相交于点O,E是BC的中点,DE交AC于F,若,则EF等于( )
A. 8 B. 6 C. 4 D. 3
图3
二. 解答题:
1. 已知:中,于D,E为AC中点,ED的延长线交AB的延长线于F。求证:(1);(2)。
2. 如图4,中,于D,E是CD的中点,AE的延长线交BC于F,,垂足为H,若,求FH。
图4
3. 如图5,N为的边BC上一点,,D为AC的中点,并且AN交BD于E。求证:。
图5
4. 在中,,延长BC至E,使,D为EC中点。求证:。
【试题答案】
一. 1. A(可求斜边长为5,斜边上的高为)
2. C(可作或)
3. B(设CD=4,则
,从而得
又
,由传递性。
故(4)、(5)、(6)正确。)
4. D
5. C(连结OE,则OE//CD且
由得)
二. 1. (1)E为AC中点,
,故
又
故
而,
(2)易得
2. 延长AC、HF交于G。
先证,可得
由E为CD的中点得,
3. 有中点时通常作平行线。
过点N作NM//BD交AC于M。
,
又
,在中,ED//NM,
,
4.
又
又
【励志故事】
把失败写在背面(一)
有一个年轻人,从很小的时候起,他就有一个梦想,希望自己能够成为一名出色的赛车手。他在军队服役的时候,曾开过卡车,这对他熟练驾驶技术起到了很大的帮助作用。
退役之后,他选择到一家农场里开车。在工作之余,他仍一直坚持参加一支业余赛车队的技能训练。只要有机会遇到车赛,他都会想尽一切办法参加。因为得不到好的名次,所以他在赛车上的收入几乎为零,这也使得他欠下一笔数目不小的债务。
那一年,他参加了威斯康星州的赛车比赛。当赛程进行到一半多的时候,他的赛车位列第三,他有很大的希望在这次比赛中获得好的名次。
突然,他前面那两辆赛车发生了相撞事故,他迅速地转动赛车的方向盘,试图避开他们。但终究因为车速太快未能成功。结果,他撞到车道旁的墙壁上,赛车在燃烧中停了下来。
当他被救出来时,手已经被烧伤,鼻子也不见了。体表伤面积达40%。医生给他做了7个小时的手术之后,才使他从死神的手中挣脱出来。
经历这次事故,尽管他命保住了,可他的手萎缩得像鸡爪一样。医生告诉他说:“以后,你再也不能开车了。”
(未完,下期待续)
