27.2.2 相似形应用举例(2)[下学期]
文档属性
| 名称 | 27.2.2 相似形应用举例(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 383.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-25 21:13:00 | ||
图片预览






文档简介
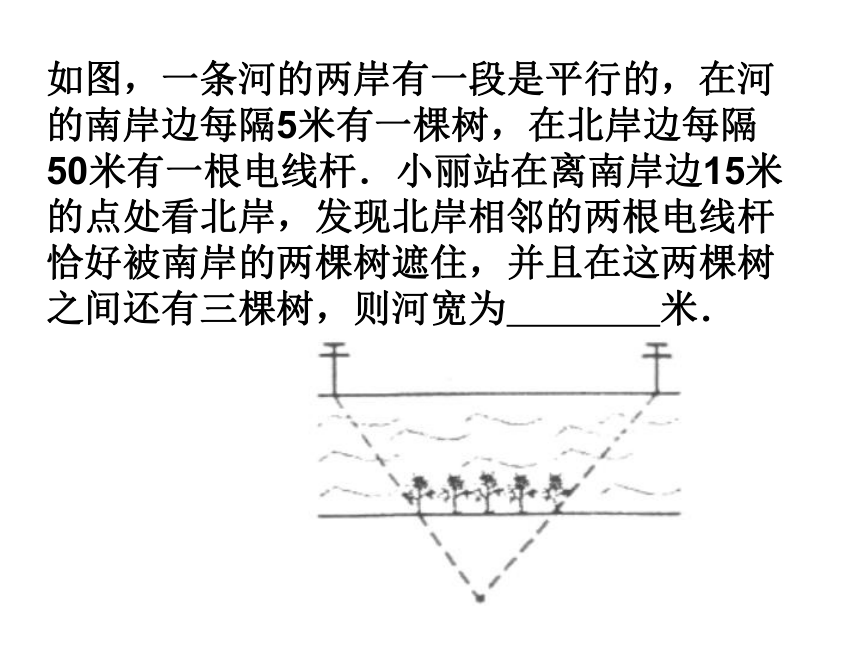
课件17张PPT。 玉环实验学校 27.2.2相似三角形的应用(2)一 温故知新复习相似三角形的条件有哪些?相似三角形有什么性质?利用相似三角形测高或测宽的一般方法是怎样?怎样利用相似三角形的有关知识测量旗杆的高度?想一想1.小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为 米.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.二 探究新知例5.已知左右并排的两棵大树高分别是AB=8cm,CD=12cm,两树的根部的距离BD=5m,一个身高1.6m的人沿着正对这两棵树的一条水平直路从左到右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C.三 同步训练例6.如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB ∥PQ.建筑物DE的一端所在直线MN垂直AB于点M,交PC于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在P点的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);(2)已知: ,求(1)中的C点到胜利街口的距离CM. 已知零件的外径为25cm,要求它的厚度x,需先求出它的内孔直径AB,现用一个交叉卡钳(AC和BD的长相等)去量(如图),若OA:OC=OB:OD=3,CD=7cm。求此零件的厚度x。 四 思维拓展www.czsx.com.cn中考透视1、如图正方形边长是2,BE=CE,MN=1。线段MN的两端在CD、AD上滑动,当DM为多长时,△ABE与以D、M、N为顶点的三角形相似。N 2、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为t秒 (0因为PN∥BC,所以△APN∽ △ABC
所以五 课时小结课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
如果P、Q分别从A、B 同时出发,移动时间为t秒 (0
所以五 课时小结课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
