相似形单元测试题[下学期]
文档属性
| 名称 | 相似形单元测试题[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 53.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-29 00:00:00 | ||
图片预览


文档简介
第27章 相似单元测试(第 4 页 共 6 页)
《相似》单元测试
姓名 总分
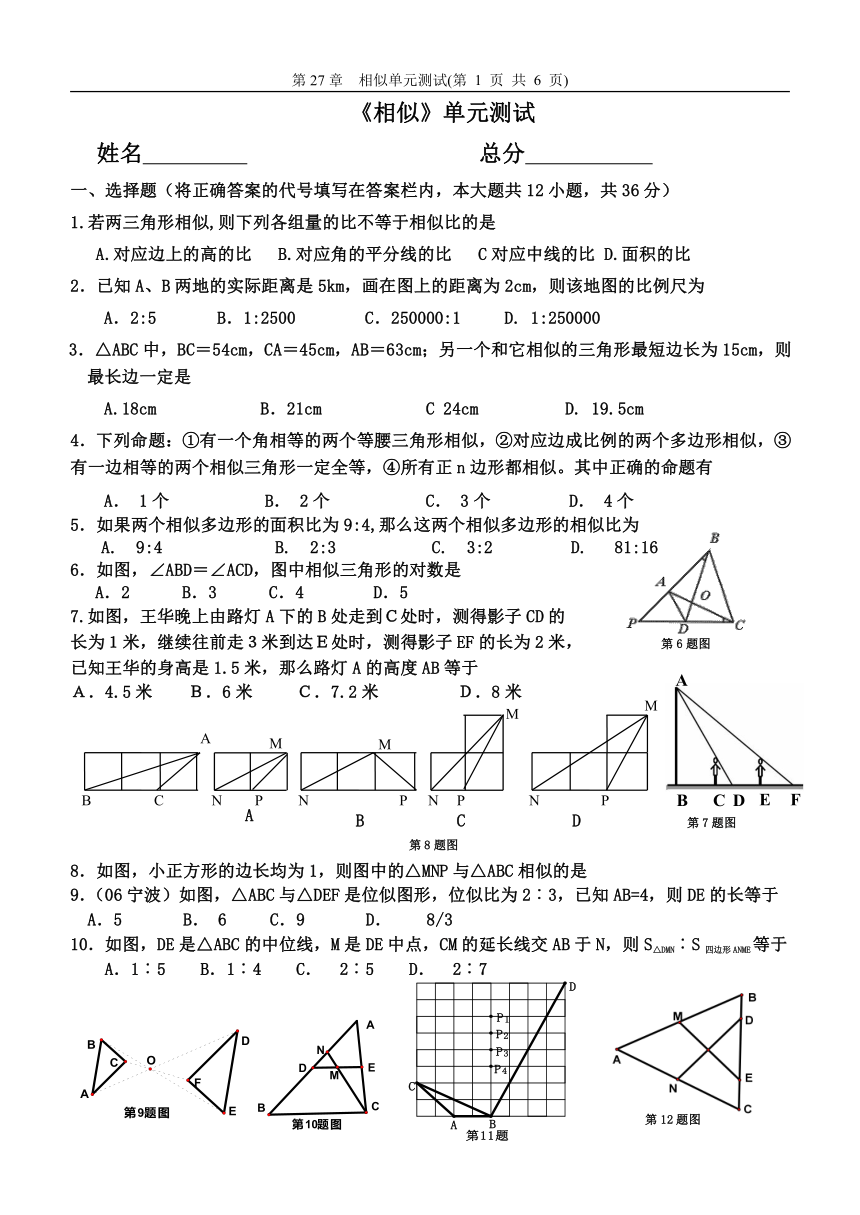
一、选择题(将正确答案的代号填写在答案栏内,本大题共12小题,共36分)
1.若两三角形相似,则下列各组量的比不等于相似比的是
A.对应边上的高的比 B.对应角的平分线的比 C对应中线的比 D.面积的比
2.已知A、B两地的实际距离是5km,画在图上的距离为2cm,则该地图的比例尺为
A.2:5 B.1:2500 C.250000:1 D. 1:250000
3.△ABC中,BC=54cm,CA=45cm,AB=63cm;另一个和它相似的三角形最短边长为15cm,则最长边一定是
A.18cm B.21cm C 24cm D. 19.5cm
4.下列命题:①有一个角相等的两个等腰三角形相似,②对应边成比例的两个多边形相似,③有一边相等的两个相似三角形一定全等,④所有正n边形都相似。其中正确的命题有
A. 1个 B. 2个 C. 3个 D. 4个
5.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为
A. 9:4 B. 2:3 C. 3:2 D. 81:16
6.如图,∠ABD=∠ACD,图中相似三角形的对数是
A.2 B.3 C.4 D.5
7.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的
长为1米,继续往前走3米到达E处时,测得影子EF的长为2米, 第6题图
已知王华的身高是1.5米,那么路灯A的高度AB等于
A.4.5米 B.6米 C.7.2米 D.8米
第7题图
第8题图
8.如图,小正方形的边长均为1,则图中的△MNP与△ABC相似的是
9.(06宁波)如图,△ABC与△DEF是位似图形,位似比为2︰3,已知AB=4,则DE的长等于
A.5 B. 6 C.9 D. 8/3
10.如图,DE是△ABC的中位线,M是DE中点,CM的延长线交AB于N,则S△DMN︰S四边形ANME等于
A.1︰5 B.1︰4 C. 2︰5 D. 2︰7
第12题图
11.如图,在正方形网格上,为使△PBD∽△ABC,则点P应在
A.P1点 B. P2点 C. P3点 D. P4点
12.(06北京)如图,在ABC中,AB=AC,M、N分别是AB、AC的中点,连结DN、EM,若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积是
A.20cm2 B. 30cm2 C. 40cm2 D. 50cm2
二填空题(共6小题,每小题3分,共18分):
13.图中的两个四边形相似,则x+y= ,a=
14.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原矩形相似,那么原来矩形的长宽比为
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6.4BD=3.6,则S△ABC=
16.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,则另外一个三角形的周长为
17.蛋糕店制作两种高度相同的圆柱形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕能够2个人吃,半径是30cm的蛋糕能够 个人吃。
18.雨后初晴,一学生在运动场上玩耍,从他前面2m远一块积水处,他看到旗杆顶端的倒影。如果旗杆底端到积水处的距离为40m,该生的眼部高度是1.5m,那么旗杆的高度是
《相似》单元测试
姓名 总分
一、选择题答题栏
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题答案:
13.x+y= ,a= 14.原来矩形的长宽比为 15.S△ABC=
16.则另外一个三角形的周长为 17.蛋糕能够 个人吃。
18.旗杆的高度是
三、解答题
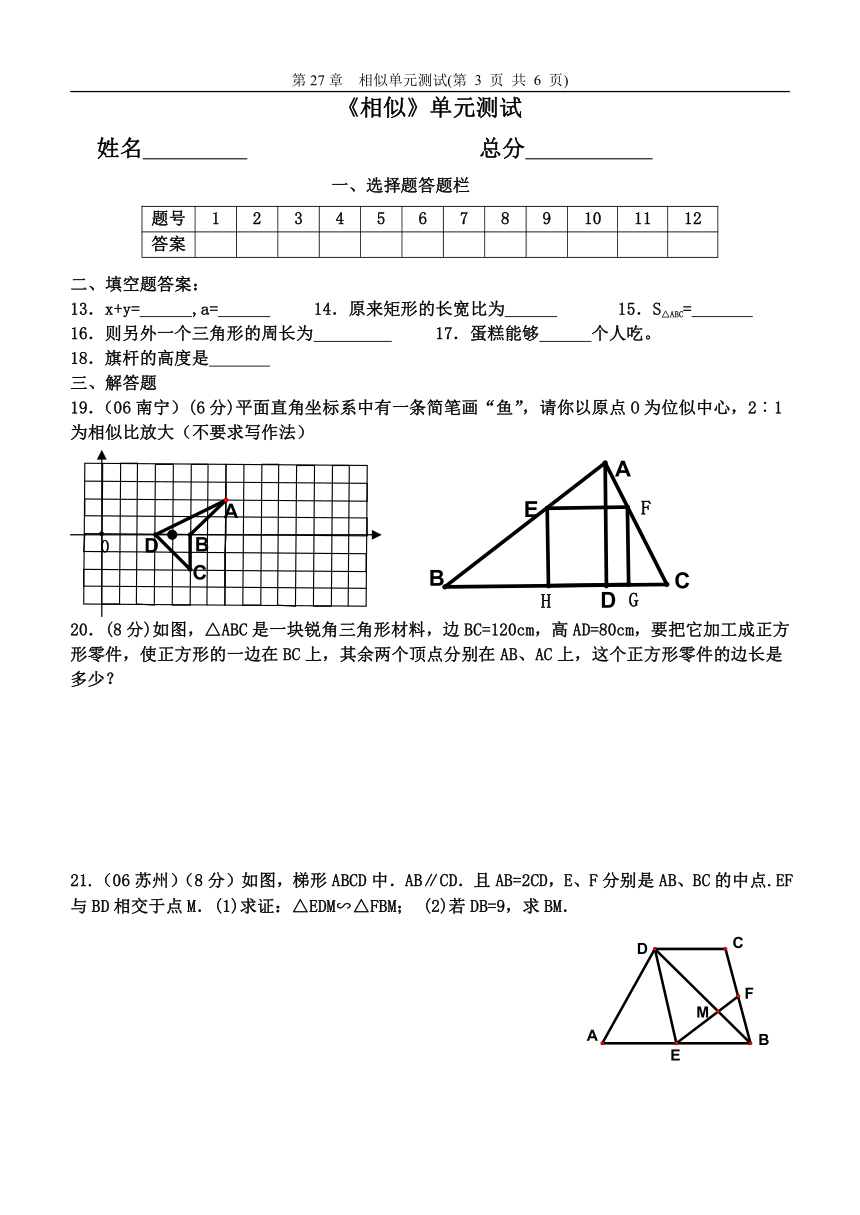
19.(06南宁)(6分)平面直角坐标系中有一条简笔画“鱼”,请你以原点O为位似中心,2︰1为相似比放大(不要求写作法)
20.(8分)如图,△ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
21.(06苏州)(8分)如图,梯形ABCD中.AB∥CD.且AB=2CD,E、F分别是AB、BC的中点.EF与BD相交于点M.(1)求证:△EDM∽△FBM; (2)若DB=9,求BM.
22(06浙江)(8分)如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE)。广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影表示),并将盲区内的那段公路设为BC,一辆以60km/h匀速行驶的汽车经过公路段BC的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离(精确到1m)
23.(8分)如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(精确到0.1米).
24、 (06青海) (8分)如图,⊙O的直径AB垂直于弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长.
25.(8分)在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么当t为何值时,△POQ与△AOB相似。
25.(2006年深圳)(12分)如图,抛物线y=ax2-8ax+12a(a<0)与x轴交于点A、B两点,(点A在点B的左侧)抛物线上另有一点C在第一象限,满足∠ACBO为直角,且恰使△OCA∽△OBC
(1)求线段OC的长;(2)在x轴上是否存在点P,使△BPC为等腰三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由。
M
A
N
B
C
P
M
N
P
M
N
P
M
N
P
A
B
D
C
D
C
B
A
F
E
D
C
B
A
《相似》单元测试
姓名 总分
一、选择题(将正确答案的代号填写在答案栏内,本大题共12小题,共36分)
1.若两三角形相似,则下列各组量的比不等于相似比的是
A.对应边上的高的比 B.对应角的平分线的比 C对应中线的比 D.面积的比
2.已知A、B两地的实际距离是5km,画在图上的距离为2cm,则该地图的比例尺为
A.2:5 B.1:2500 C.250000:1 D. 1:250000
3.△ABC中,BC=54cm,CA=45cm,AB=63cm;另一个和它相似的三角形最短边长为15cm,则最长边一定是
A.18cm B.21cm C 24cm D. 19.5cm
4.下列命题:①有一个角相等的两个等腰三角形相似,②对应边成比例的两个多边形相似,③有一边相等的两个相似三角形一定全等,④所有正n边形都相似。其中正确的命题有
A. 1个 B. 2个 C. 3个 D. 4个
5.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为
A. 9:4 B. 2:3 C. 3:2 D. 81:16
6.如图,∠ABD=∠ACD,图中相似三角形的对数是
A.2 B.3 C.4 D.5
7.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的
长为1米,继续往前走3米到达E处时,测得影子EF的长为2米, 第6题图
已知王华的身高是1.5米,那么路灯A的高度AB等于
A.4.5米 B.6米 C.7.2米 D.8米
第7题图
第8题图
8.如图,小正方形的边长均为1,则图中的△MNP与△ABC相似的是
9.(06宁波)如图,△ABC与△DEF是位似图形,位似比为2︰3,已知AB=4,则DE的长等于
A.5 B. 6 C.9 D. 8/3
10.如图,DE是△ABC的中位线,M是DE中点,CM的延长线交AB于N,则S△DMN︰S四边形ANME等于
A.1︰5 B.1︰4 C. 2︰5 D. 2︰7
第12题图
11.如图,在正方形网格上,为使△PBD∽△ABC,则点P应在
A.P1点 B. P2点 C. P3点 D. P4点
12.(06北京)如图,在ABC中,AB=AC,M、N分别是AB、AC的中点,连结DN、EM,若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积是
A.20cm2 B. 30cm2 C. 40cm2 D. 50cm2
二填空题(共6小题,每小题3分,共18分):
13.图中的两个四边形相似,则x+y= ,a=
14.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原矩形相似,那么原来矩形的长宽比为
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6.4BD=3.6,则S△ABC=
16.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,则另外一个三角形的周长为
17.蛋糕店制作两种高度相同的圆柱形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕能够2个人吃,半径是30cm的蛋糕能够 个人吃。
18.雨后初晴,一学生在运动场上玩耍,从他前面2m远一块积水处,他看到旗杆顶端的倒影。如果旗杆底端到积水处的距离为40m,该生的眼部高度是1.5m,那么旗杆的高度是
《相似》单元测试
姓名 总分
一、选择题答题栏
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题答案:
13.x+y= ,a= 14.原来矩形的长宽比为 15.S△ABC=
16.则另外一个三角形的周长为 17.蛋糕能够 个人吃。
18.旗杆的高度是
三、解答题
19.(06南宁)(6分)平面直角坐标系中有一条简笔画“鱼”,请你以原点O为位似中心,2︰1为相似比放大(不要求写作法)
20.(8分)如图,△ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
21.(06苏州)(8分)如图,梯形ABCD中.AB∥CD.且AB=2CD,E、F分别是AB、BC的中点.EF与BD相交于点M.(1)求证:△EDM∽△FBM; (2)若DB=9,求BM.
22(06浙江)(8分)如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE)。广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影表示),并将盲区内的那段公路设为BC,一辆以60km/h匀速行驶的汽车经过公路段BC的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离(精确到1m)
23.(8分)如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(精确到0.1米).
24、 (06青海) (8分)如图,⊙O的直径AB垂直于弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长.
25.(8分)在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么当t为何值时,△POQ与△AOB相似。
25.(2006年深圳)(12分)如图,抛物线y=ax2-8ax+12a(a<0)与x轴交于点A、B两点,(点A在点B的左侧)抛物线上另有一点C在第一象限,满足∠ACBO为直角,且恰使△OCA∽△OBC
(1)求线段OC的长;(2)在x轴上是否存在点P,使△BPC为等腰三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由。
M
A
N
B
C
P
M
N
P
M
N
P
M
N
P
A
B
D
C
D
C
B
A
F
E
D
C
B
A
