【专项】二次函数的实际应用解答题专项练习 (含解析)
文档属性
| 名称 | 【专项】二次函数的实际应用解答题专项练习 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 11:59:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数的实际应用解答题专项练习
1.北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民喜爱.某特许零售店“冰墩墩的销售日益火爆.每个纪念品进价40元,规定销售单价不低于48元,且不高于56.5元.销售期间发现,当销售单价定为48元时,每天可售230个,销售单价每上涨1元,每天销量减少10个.现商家提价销售,设每天销售量为y个,销售单价为x元.
(1)填空:y与x之间的函数关系式是 ;自变量x的取值范围是 .
(2)将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?
2.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
3.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x(元),月销售利润为y(元),求y与x的函数关系式;
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)销售单价定为多少时,月销售利润最大?利润最大值为多少?
4.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克.
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足y=﹣10x+840,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
5.大鹏童装店销售某款童装每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖出10件,已知该款童装每件成本30元,设该款童装每件售价x元每星期销售量为y件.
(1)求y与x之间的函数关系式;
(2)若商店按每件售价不超过45元来销售,当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该童装多少件?
6.在运动会比赛时,九年级的一名男同学推铅球,已知铅球经过的路线是某二次函数图象的一部分(如图所示),如果这名男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5).
(1)求出这个二次函数的解析式;
(2)请求出这名男同学比赛时的成绩?
7.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.中国18岁小将苏翊鸣获得冠军.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
这是苏翊鸣参赛前进行的一次训练.
(1)训练时,苏翊鸣的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出苏翊鸣竖直高度的最大值,并求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)训练时,苏翊鸣的着陆点的竖直高度为7米,求着陆点的水平距离为多少?
8.如图,交易会上主办方利用足够长的一段围墙,用围栏围成一个长方形的空地,中间用围栏分割出2个小长方形展厅,并且在与墙平行的一边上各开了一扇宽为1.5m的门,总共用去围栏36m.
(1)若长方形展厅ABCD的面积为90m2,求边AB的长为多少米?
(2)当边AB的长为多少米时,长方形展厅ABCD的面积最大?
9.如图,小区中央公园要修建一个圆形的喷水池,在水池中央垂直于地面安装一个柱子OA,O恰好在水面的中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计水流在离OA距离为1米处达到距水面的最大高度2.25米.
(1)求抛物线的解析式;
(2)若不计其他因素,则水池的半径至少要多少米才能使喷出的水流不至于落到池外?
10.某游乐场的圆形喷水池中心O有一喷水管OA,从点A四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+2.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
(3)现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?
11.如图,有一座抛物线形状的拱桥,对拱桥在水面以上的部分进行测量,得到桥洞的跨度为12米,并且以桥洞拱顶为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系,把测量得到的数据记入表:
x(米) ﹣6 ﹣4 ﹣2 0 2 4 6
y(米) ﹣3.02 ﹣1.33 ﹣0.31 0 ﹣0.32 ﹣1.33 ﹣2.99
(1)请在下面的坐标系中根据已知数据描点,并用平滑的曲线连接;
(2)请结合图象,写出拱桥的桥洞在拱顶下方1米的位置宽度是 米(结果精确到0.1);
(3)现有一艘宽4米,高2米的游船要穿过拱桥的桥洞.为保证安全,要求船顶到竖直方向上拱桥桥洞对应点的距离不小于0.5米,那么这艘船 (填“能”或者“不能”)安全通过.
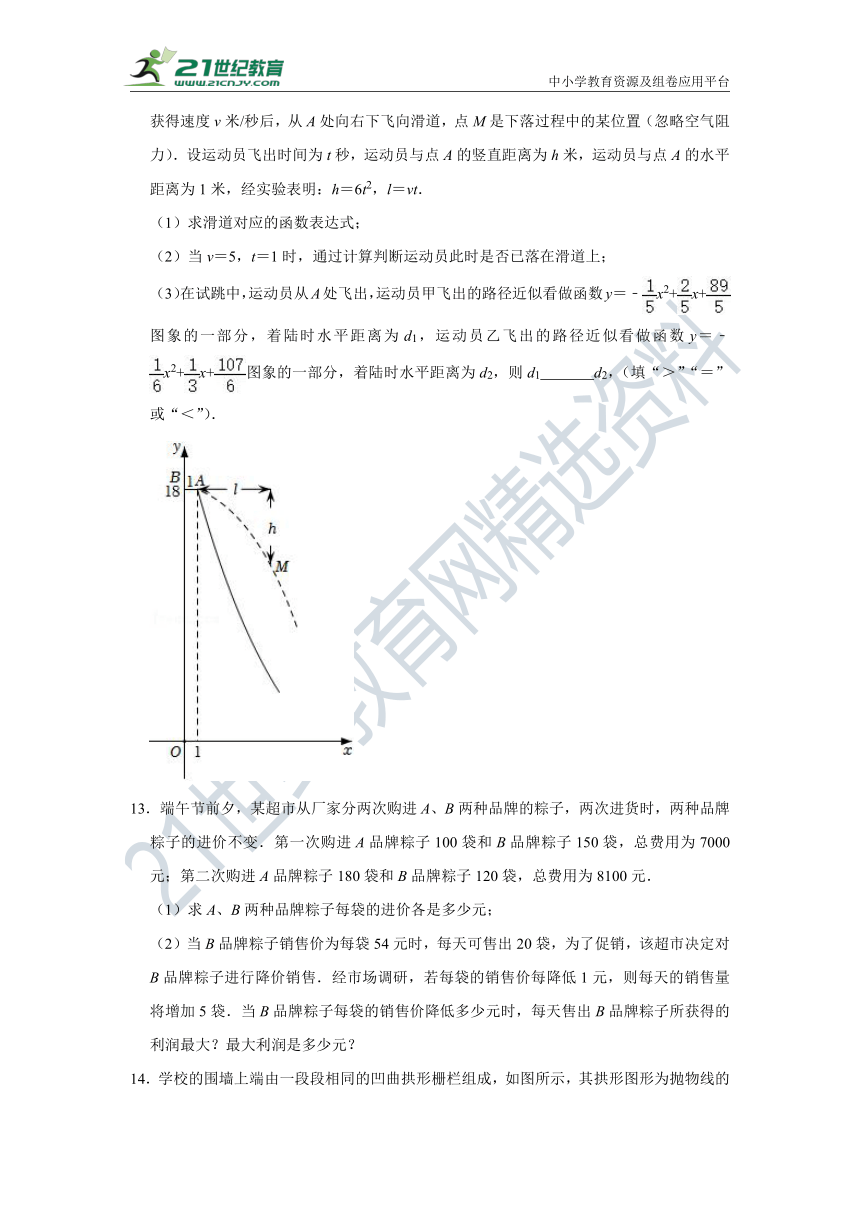
12.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,如图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系,已知滑道对应的函数为y=x2﹣4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为1米,经实验表明:h=6t2,l=vt.
(1)求滑道对应的函数表达式;
(2)当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;
(3)在试跳中,运动员从A处飞出,运动员甲飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d1,运动员乙飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d2,则d1 d2,(填“>”“=”或“<”).
13.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
14.学校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.5米用5根立柱加固,拱高OC为米.
(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2对应的函数表达式;
(2)请计算一段棚栏所需5很立柱的总长度L.
15.某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为6元/kg,每日销售y/(kg)与销售单价x(元/kg)满足关系式:y=kx+b,部分数据如表:
销售单价x(元/kg) 1 2 … 10
每日销售量(kg) 4900 4800 … 4000
经销售发现,销售单价不低于成本价格且不高于30元/kg.设该食品公司销售这种瓜子的日获利为w(元).
(1)y与x的函数关系式是 ,x的范围是 ;w与x的函数关系式是 ;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司可收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,直接写出a的值.
16.大同南城墙永泰门广场的音乐喷泉,因为有古城墙做背景,成为古都大同美丽特别的风景.如图是其中一个喷泉的示意图,喷泉有一个竖直的喷水枪AB,喷水口为A,喷出水流的运动路线是抛物线,如果水流的最高点P到AB所在直线的距离为1m,且到地面的距离为3.6m,水流的落地点C到喷水枪底部B的距离为2.5m,喷水枪AB应为多长?请你在以BC所在直线为x轴,AB所在直线为y轴的平面直角坐标系中解决问题.
17.据统计,某景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:
购票方式 甲 乙 丙
可游玩景点 A B A和B
门票价格 100元/人 80元/人 160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
18.云南某星级酒店共有50个房间供给受疫情影响需要隔离的人员居住,每间房价不低于200元且不超过350元,酒店还需对隔离人员居住的每个房间每天支出各种费用共计120元已知需要隔离的人员居住的房间数y(单位:间)和每个房间定价x(单位:元)符合一次函数关系,如图是y关于x的函数图象.
(1)求y与x之间的函数解析式;
(2)当房价定为多少元时,酒店利润最大?最大利润是多少元?
19.某商场销售一种季节性产品,以下是该产品在销售期(30天)内的部分信息:
①第x天(x为整数)的销量为(40+2x)千克;
②该产品前10天的售价都是50元千克,从第11天开始售价y(元/千克)是第x天的一次函数,对应关系如表:
第x天 15 20
售价y(元/千克) 45 40
(1)当11≤x≤30时,求出y与x的关系式;
(2)当x为何值时日销售额w最大,最大为多少?
20.今年某市疫情形势严峻,物资紧缺.为保障物资供应,相关部门加强蔬菜抢种和抢收力度,建议取消蔬菜采收后养地的传统做法,采用采收后立即播种的新种植方式.当季某种蔬菜的适宜生育温度为15℃﹣30℃,在平均温度20℃时,传统种植方式平均产量为2500千克/亩,采用新种植方式后,平均产量为a千克/亩.已知A公司在郊区承包该种蔬菜种植面积50亩,其中30亩采用新种植方式,这50亩共采收蔬菜110000千克.
(1)平均温度20℃时,求该种蔬菜采用新种植方式每亩的平均产量;
(2)采用新种植方式的蔬菜原计划在5月15日上市,为提前上市应对需求的激增,A公司启动大棚内智能化控温设备,缩短蔬菜生长周期.经调查,当平均温度超过20℃时,温度升高会导致蔬菜幼苗成活率下降,每升高1℃,平均每亩产量减少50千克;提前上市的天数y(天)与温度t(℃)满足y=﹣t2+30t﹣360(20≤t≤30).为了确保蔬菜所需的供应量,要求平均产量不低于1600千克/亩,判断这批蔬菜能否在5月1日上市?并说明理由.
21.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y件,销售该商品的每天利润为w元.
(1)第x(1≤x≤30)天的销售价为每件 元,这段时间每天的销售量y(件)与x(天)的函数关系式为 ;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
22.某校开展助力贫困儿童的爱心义卖活动,七(1)班班委组织了33名同学制作甲、乙两种作品,其中每人可制作1件甲作品或2件乙作品.已知制作4件甲作品,每件甲作品可获利20元;当甲作品每多制作一件时,平均每件获利减少0.5元(甲作品制作不少于4件);乙作品每件可获利5元.设安排x人生产甲作品.
(1)完成下列表格(用含x的代数式表示):
作品种类 人数(人) 制作量(件) 每件产品可获利润(元)
甲 x
乙 5
(2)若制作甲作品可获得的总利润比制作乙作品可获得的总利润多20元,求制作甲作品的人数;
(3)在不改变总人数的情况下,增加制作丙作品,每人可制作1件丙作品(每位同学只制作一种类型的作品),已知丙作品每件可获利13元.若制作乙、丙作品的件数相等,则制作丙作品的同学有 人(用含x的代数式表示),当全部作品都卖完时,总利润的最大值为 元(直接写出答案).
23.“贵妃芒”芒果品种是广受各地消费者青睐的优质新品种,在我国海南省广泛种植,某水果商以每斤15元的价格从该省批发“贵妃芒”,再按每斤25元价格到市区销售,平均每天可售出60斤,经过调查发现,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.设“贵妃芒”每斤的价格降低x元.
(1)则每天的销售量是 斤(用含x的代数式表示);
(2)水果商销售“贵妃芒”每天盈利630元,每斤“贵妃芒”的售价应降至每斤多少元?(其他成本忽略不计)
(3)若x的范围为1≤x≤9的正整数,请直接写出水果商的最高利润与最低利润的差为 元.
24.浙江省温州市是全国旅游胜地,2020年受新冠疫情的影响,来温的外来游客在逐年下降.某景区外来游客人数从2019年的2.25万下降到2021年的1.44万.
(1)求2019年到2021年该景区外来游客人数平均每年降低的百分率;
(2)该景区要建一个游乐场(如图所示),其中AD、CD分别靠现有墙DM、DN(墙DM长为27米,墙DN足够长),其余用篱笆围成.篱笆DE将游乐场隔成等腰直角△CED和长方形ADEB两部分,并在三处各留2米宽的大门.已知篱笆总长为54米.
①当AB多长时,游乐场的面积为320平方米?
②当AB= 米时,游乐场的面积达到最大,最大为 平方米.
25.2022年中秋节,某超市销售一种月饼,成本每千克40元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 55 60
销售量y(千克) 100 90 80
(1)求y与x之间的函数关系式;
(2)物价局规定这种月饼售价每千克不高于65元.设这种月饼每天的利润为W(元),求W与x之间的函数关系式,并求出当售价为多少元时获得最大利润,最大利润是多少?
26.一商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x (元/件) (x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 4 5 6
y(件) 1000 950 900
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件,求这一周市商场销售这种商品获得的最大利润和售价分别为多少元?
答 案
1.北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民喜爱.某特许零售店“冰墩墩的销售日益火爆.每个纪念品进价40元,规定销售单价不低于48元,且不高于56.5元.销售期间发现,当销售单价定为48元时,每天可售230个,销售单价每上涨1元,每天销量减少10个.现商家提价销售,设每天销售量为y个,销售单价为x元.
(1)填空:y与x之间的函数关系式是 y=﹣10x+710 ;自变量x的取值范围是 48≤x≤56.5 .
(2)将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?
解:(1)根据题意得:y=230﹣10(x﹣48)=﹣10x+710,
∴y与x之间的函数关系式为y=﹣10x+710(48≤x≤56.5);
故答案为:y=﹣10x+710;48≤x≤56.5;
(2)根据题意得:w=(﹣10x+710)(x﹣40)=﹣10x2+1110x﹣28400=﹣10(x﹣55.5)2+2402.5,
∵﹣10<0,
∴当x<55.5时,w随x的增大而增大,
∵48≤x≤56.5,
∴当x=55.5时,w有最大值,最大值为2402.5,
∴将纪念品的销售单价定为55.5元时,商家每天销售纪念品获得的利润w元最大,最大利润是2402.5元.
2.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
解:(1)根据题意得,y=60﹣2x;
(2)设茶商每天的利润为w元,根据题意得,w=(20+x)(﹣2x+60)=﹣2(x﹣5)2+1250,
∵a=﹣2<0,
∴当x=5时,w最大=1250元,
答:该茶商每天的最大利润为1250元.
3.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x(元),月销售利润为y(元),求y与x的函数关系式;
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)销售单价定为多少时,月销售利润最大?利润最大值为多少?
解:(1)由题意可得:
y=(x﹣40)[500﹣(x﹣50)×10]=﹣10x2+1400x﹣40000,
答:y与x的函数关系式是:y=﹣10x2+1400x﹣40000;
(2)将y=8000代入y=﹣10x2+1400x﹣40000,得,
﹣10x2+1400x﹣40000=8000,
解得,x=60或x=80,
又∵40×[500﹣(x﹣50)×10]≤10000,
解得:x≥75,
∴定价为每千克80元,
答:在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为80元;
(3)∵y=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∴当x=70时,月销售利润最大,最大利润是9000,
答:销售单价定为每千克70元时,月销售利润达到最大为9000.
4.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克.
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足y=﹣10x+840,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
解:(1)设现在实际购进这种牛肉每千克a元,则原来购进这种牛肉每千克(a+2)元,
由题意得:32(a+2)=33a,
解得:a=64(元),
答:现在实际购进这种牛肉每千克64元;
(2)设销售利润为w元,由题意得
w=(x﹣64)y=(x﹣64)(﹣10x+840)=﹣10x2+1480x﹣53760=﹣10(x﹣74)2+1000,
所以当x=74时,w有最大值1000.
答:将这种牛肉的销售单价定为74元时,能获得最大利润,最大利润是1000元.
5.大鹏童装店销售某款童装每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖出10件,已知该款童装每件成本30元,设该款童装每件售价x元每星期销售量为y件.
(1)求y与x之间的函数关系式;
(2)若商店按每件售价不超过45元来销售,当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该童装多少件?
解:(1)y=100+10(60﹣x)=﹣10x+700;
(2)设每星期利润为W元,
W=(x﹣30)(﹣10x+700)=﹣10(x﹣50)2+4000,
当x≤45时,W随x的增大而增大,
∴x=545时,W最大值=﹣10×(45﹣50)2+4000=3750,
当每件售价为45元时,每星期的销售利润最大,最大利润3750元;
(3)①由题意:﹣10(x﹣50)2+4000=3910,
解得:x=53或47,
∴当每件童装售价定为53元或47元时,该店一星期可获得3910元的利润.
②由题意:﹣10(x﹣50)2+4000≥3910,
解得:47≤x≤53,
∵y=100+10(60﹣x)=﹣10x+700.
170≤y≤230,
∴每星期至少要销售该款童装170件.
6.在运动会比赛时,九年级的一名男同学推铅球,已知铅球经过的路线是某二次函数图象的一部分(如图所示),如果这名男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5).
(1)求出这个二次函数的解析式;
(2)请求出这名男同学比赛时的成绩?
解:(1)设二次函数的解析式为y=a(x﹣h)2+k,
由于顶点坐标为(6,5),
∴y=a(x﹣6)2+5.
又A(0,2)在抛物线上,
∴2=62 a+5,
解得:a=﹣.
∴二次函数的解析式为y=﹣(x﹣6)2+5,
整理得:y=﹣x2+x+2.
∴这个二次函数的解析式是y=﹣x2+x+2;
(2)当y=0时,﹣x2+x+2=0.
∴x1=6+2,x2=6﹣2(不合题意,舍去).
答:这名男同学比赛时的成绩是(6+2)米.
7.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.中国18岁小将苏翊鸣获得冠军.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
这是苏翊鸣参赛前进行的一次训练.
(1)训练时,苏翊鸣的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出苏翊鸣竖直高度的最大值,并求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)训练时,苏翊鸣的着陆点的竖直高度为7米,求着陆点的水平距离为多少?
解:(1)根据表格中的数据可知,抛物线的顶点坐标为:(8,23.20),
∴h=8,k=23.20,
即该运动员竖直高度的最大值为23.20m,
根据表格中的数据可知,当x=0时,y=20.00,代入y=a(x﹣8)2+23.20得:
20.00=a(0﹣8)2+23.20,
解得:a=﹣0.05,
∴函数关系式为:y=﹣0.05(x﹣8)2+23.20;
(2)把y=7代入y=﹣0.05(x﹣8)2+23.20,
解得:x=26或x=﹣18(不符合题意舍去),
∴着落点的水平距离为26米.
8.如图,交易会上主办方利用足够长的一段围墙,用围栏围成一个长方形的空地,中间用围栏分割出2个小长方形展厅,并且在与墙平行的一边上各开了一扇宽为1.5m的门,总共用去围栏36m.
(1)若长方形展厅ABCD的面积为90m2,求边AB的长为多少米?
(2)当边AB的长为多少米时,长方形展厅ABCD的面积最大?
解:(1)设AB的长为x米,
则BC=36﹣3x+2×1.5=(39﹣3x)米,
根据题意得(39﹣3x)x=90,
解得x1=3,x2=10,
答:AB的长为3或10米;
(2)∵长方形展厅ABCD的面积=(39﹣3x)x=﹣3x2+39x=﹣3(x﹣)2+,
对称轴为x=,
∴当米时,所围成的长方形展厅ABCD的面积最大.
9.如图,小区中央公园要修建一个圆形的喷水池,在水池中央垂直于地面安装一个柱子OA,O恰好在水面的中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计水流在离OA距离为1米处达到距水面的最大高度2.25米.
(1)求抛物线的解析式;
(2)若不计其他因素,则水池的半径至少要多少米才能使喷出的水流不至于落到池外?
解:(1)∵顶点为(1,2.25),
∴设解析式为y=a(x﹣1)2+2.25,
∵函数过点(0,1.25),
∴代入解析式解得a=﹣1,
∴解析式为:y=﹣(x﹣1)2+2.25;
(2)由(1)可知:y=﹣(x﹣1)2+2.25,
令y=0,则﹣(x﹣1)2+2.25=0,
解得x=2.5或x=﹣0.5(舍去),
所以花坛的半径至少为2.5m才能使喷出的水流不至于落到池外.
10.某游乐场的圆形喷水池中心O有一喷水管OA,从点A四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+2.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
(3)现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?
解:(1)当x=0时,y=﹣×(0﹣3)2+2=,
∴点A的坐标为(0,),
∴喷水管高OA高m.
(2)解法一:对于y=﹣(x﹣3)2+2,
令x=4,则y=﹣(4﹣3)2+2=>1.7,
∴小明不会被水喷到;
解法二:令y=1.7,
则﹣(x﹣3)2+2=1.7,
解得:x1=3+,x2=3﹣,
∵3+>4,3﹣<4,
∴小明不会被水喷到;
(3)设喷水管OA的高度要升高hm,
则抛物线的表达式为y=﹣(x﹣3)2+2+h.
把(7,0)代入得:0=﹣(x﹣3)2+2+h,
解得:h=,
∴喷水管OA的高度要升高m.
11.如图,有一座抛物线形状的拱桥,对拱桥在水面以上的部分进行测量,得到桥洞的跨度为12米,并且以桥洞拱顶为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系,把测量得到的数据记入表:
x(米) ﹣6 ﹣4 ﹣2 0 2 4 6
y(米) ﹣3.02 ﹣1.33 ﹣0.31 0 ﹣0.32 ﹣1.33 ﹣2.99
(1)请在下面的坐标系中根据已知数据描点,并用平滑的曲线连接;
(2)请结合图象,写出拱桥的桥洞在拱顶下方1米的位置宽度是 6.8 米(结果精确到0.1);
(3)现有一艘宽4米,高2米的游船要穿过拱桥的桥洞.为保证安全,要求船顶到竖直方向上拱桥桥洞对应点的距离不小于0.5米,那么这艘船 能 (填“能”或者“不能”)安全通过.
解:(1)用描点法作图如下:
(2)由图象可得,拱桥的桥洞在拱顶下方1米的位置宽度是6.8米;
(3)由表中数据知当x=±2时,y=﹣0.32,
当x=±6时,y=﹣2.99,
﹣0.32﹣(﹣2.99)=﹣0.32+2.99=2.67,
∵2.67﹣2=0.67>2,
∴这艘船能安全通过.
故答案为:能.
12.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,如图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系,已知滑道对应的函数为y=x2﹣4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为1米,经实验表明:h=6t2,l=vt.
(1)求滑道对应的函数表达式;
(2)当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;
(3)在试跳中,运动员从A处飞出,运动员甲飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d1,运动员乙飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d2,则d1 < d2,(填“>”“=”或“<”).
解:(1)由题意得:A(1,18),
把A(1,18)代入解析式得:×12﹣4×1+c=18,
解得:c=21.8,
∴滑道对应的函数表达式为y=x2﹣4x+21.8;
(2)当v=5,t=1时,h=6t2=6,l=vt=5,
当x=6时,y=×62﹣4×6+21.8=5,
而18﹣h=18﹣6=12>5,
∴运动员此时未落在滑道上;
(3)对于y=﹣x2+x+,
令y=0,则﹣x2+x+=0,
解得x=1±3,
∴d1=1+3;
对于y=﹣x2+x+,
令y=0,则﹣x2+x+=0,
解得x=1+6,
∴d2=1+6,
∵d1=1+,d2=1+,
∴d1<d2.
故答案为:<.
13.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
解:(1)A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元,
根据题意得,,
解得,
答:A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元;
(2)设B品牌粽子每袋的销售价降低a元时,每天售出B品牌粽子所获得的利润最大,利润为w元,
根据题意得,w=(54﹣a﹣30)(20+5a)=﹣5a2+100a+480=﹣5(a﹣10)2+980,
∵﹣5<0,
∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980元.
14.学校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.5米用5根立柱加固,拱高OC为米.
(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2对应的函数表达式;
(2)请计算一段棚栏所需5很立柱的总长度L.
解:(1)由已知:OC=米,AC=1.5,
得点A的坐标为(1.5,),
代入y=ax2,
得a=,
∴抛物线的解析式为y=x2;
(2)点C1,C2的横坐标分别为0.5,1,
代入y=x2,
得点C1,C2的纵坐标分别为:
y1=×0.52=0.2,y2=×12=0.8,
∴立柱C1D1=﹣0.2=1.6,C2D2=﹣0.8=1,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:2(C1D1+C2D2)+OC=2(1.6+1)+1.8=7(米).
15.某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为6元/kg,每日销售y/(kg)与销售单价x(元/kg)满足关系式:y=kx+b,部分数据如表:
销售单价x(元/kg) 1 2 … 10
每日销售量(kg) 4900 4800 … 4000
经销售发现,销售单价不低于成本价格且不高于30元/kg.设该食品公司销售这种瓜子的日获利为w(元).
(1)y与x的函数关系式是 y=﹣100x+5000 ,x的范围是 x>1 ;w与x的函数关系式是 w=﹣100x2+5600x﹣32000(6≤x≤30) ;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司可收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,直接写出a的值.
解:(1)由表中数据可得,当x=1时,y=4900,当x=2时,y=4800,代入y=kx+b得,
,
解得,
∴y与x的函数关系式是y=﹣100x+5000,且x>1;
由于销售单价不低于成本价格(6元>且不高于30元/kg,
则w=(x﹣6)(﹣100x+5000)﹣2000
=﹣100x2+5600x﹣32000(6≤x≤30).
故答案为:y=﹣100x+5000;x>1;w=﹣100x2+5600x﹣32000(6≤x≤30).
(2)由(1)知,w=﹣100x2+5600x﹣32000(6≤x≤30).
∵a=﹣100<0,
∴函数图象开口向下,有最大值,
函数图象的对称轴为x=﹣=28,
∵6≤x≤30,
∴当x=28时,函数w有最大值,为46400,
∴销售单价定位28元时,获利最大,为46400元;
(3)收取α元后,利润为w=(x﹣6﹣a)(﹣100x+5000)﹣2000=﹣100x2+(5600+100a)x﹣32000﹣5000a,
∵a=﹣100<0,
∴函数图象开口向下,有最大值,
又函数图象的对称轴为x=﹣=28+a,
∵a<4,
∴当x=28+a时,获利最大值为42100元,
将x=28+a代入得,(28+a﹣6﹣a)[﹣100(28+a)+5000]﹣2000=42100,
解得a=2或a=6(舍),
∴a=2.
16.大同南城墙永泰门广场的音乐喷泉,因为有古城墙做背景,成为古都大同美丽特别的风景.如图是其中一个喷泉的示意图,喷泉有一个竖直的喷水枪AB,喷水口为A,喷出水流的运动路线是抛物线,如果水流的最高点P到AB所在直线的距离为1m,且到地面的距离为3.6m,水流的落地点C到喷水枪底部B的距离为2.5m,喷水枪AB应为多长?请你在以BC所在直线为x轴,AB所在直线为y轴的平面直角坐标系中解决问题.
解:如图:
由题意知,抛物线的顶点P的坐标为(1,3.6)、点C(2.5,0),
设抛物线的解析式为y=a(x﹣1)2+3.6,
将点C(2.5,0)代入,得:2.25a+3.6=0,
解得:a=﹣1.6,
则抛物线的解析式为y=﹣1.6(x﹣1)2+3.6;
当x=0时,有y=﹣1.6(0﹣1)2+3.6=2,
∴AB=2,
答:喷水枪AB应为2m.
17.据统计,某景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:
购票方式 甲 乙 丙
可游玩景点 A B A和B
门票价格 100元/人 80元/人 160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
解:①由题意得:
100×(2﹣10×0.06)+80×(3﹣10×0.04)+(160﹣10)×(2+10×0.06+10×0.04)=798(万元).
答:景区六月份的门票总收入为798万元;
②设丙种门票价格降低x元,景区六月份的门票总收入为W万元,
由题意,得
W=100(2﹣0.06x)+80(3﹣0.04x)+(160﹣x)(2+0.06x+0.04x),
化简,得W=﹣0.1(x﹣24)2+817.6,
∵﹣0.1<0,
∴当x=24时,W取最大值,为817.6万元.
答:当丙种门票价格下降24元时,景区六月份的门票总收入有最大值,最大值是817.6万元.
18.云南某星级酒店共有50个房间供给受疫情影响需要隔离的人员居住,每间房价不低于200元且不超过350元,酒店还需对隔离人员居住的每个房间每天支出各种费用共计120元已知需要隔离的人员居住的房间数y(单位:间)和每个房间定价x(单位:元)符合一次函数关系,如图是y关于x的函数图象.
(1)求y与x之间的函数解析式;
(2)当房价定为多少元时,酒店利润最大?最大利润是多少元?
解:(1)由题意,设y关于x的函数解析式为y=kx+b,
把(280,40),(290,38)代入得:
,
解得:,
∴y与x之间的函数解析式为y=﹣x+96(230≤x≤350);
(2)设酒店的利润为w元,
则w=(x﹣120)y=(x﹣120)(﹣x+96)=﹣x2+120x﹣11520=﹣(x﹣300)2+6480,
∵﹣<0,230≤x≤350
∴当x=300时,w取得最大值,最大值为6480元,
答:当每间房价定价为300元时,酒店每天所获利润最大,最大利润是6480元.
19.某商场销售一种季节性产品,以下是该产品在销售期(30天)内的部分信息:
①第x天(x为整数)的销量为(40+2x)千克;
②该产品前10天的售价都是50元千克,从第11天开始售价y(元/千克)是第x天的一次函数,对应关系如表:
第x天 15 20
售价y(元/千克) 45 40
(1)当11≤x≤30时,求出y与x的关系式;
(2)当x为何值时日销售额w最大,最大为多少?
解:(1)当11≤x≤30时,设y与x的关系式为y=kx+b,
将(15,45),(20,40)代入得:
,
解得,
∴y=﹣x+60(11≤x≤30);
(2)当1≤x≤10时,w=50(40+2x)=100x+2000,
∵100>0,
∴w随x的增大而增大,
∴x=10时,w最大为100×10+2000=3000(元),
当11≤x≤30时,w=(﹣x+60)(40+2x)=﹣2(x﹣20)2+3200,
∵﹣2<0,
∴x=20时,w取最大值3200,
∵3000<3200,
∴x为20时日销售额w最大,最大为3200元.
20.今年某市疫情形势严峻,物资紧缺.为保障物资供应,相关部门加强蔬菜抢种和抢收力度,建议取消蔬菜采收后养地的传统做法,采用采收后立即播种的新种植方式.当季某种蔬菜的适宜生育温度为15℃﹣30℃,在平均温度20℃时,传统种植方式平均产量为2500千克/亩,采用新种植方式后,平均产量为a千克/亩.已知A公司在郊区承包该种蔬菜种植面积50亩,其中30亩采用新种植方式,这50亩共采收蔬菜110000千克.
(1)平均温度20℃时,求该种蔬菜采用新种植方式每亩的平均产量;
(2)采用新种植方式的蔬菜原计划在5月15日上市,为提前上市应对需求的激增,A公司启动大棚内智能化控温设备,缩短蔬菜生长周期.经调查,当平均温度超过20℃时,温度升高会导致蔬菜幼苗成活率下降,每升高1℃,平均每亩产量减少50千克;提前上市的天数y(天)与温度t(℃)满足y=﹣t2+30t﹣360(20≤t≤30).为了确保蔬菜所需的供应量,要求平均产量不低于1600千克/亩,判断这批蔬菜能否在5月1日上市?并说明理由.
解:(1)根据题意得:30a+(50﹣30)×2500=110000,
解得a=2000,
答:平均温度20℃时,该种蔬菜采用新种植方式每亩的平均产量是2000千克;
(2)∵每升高1℃,平均每亩产量减少50千克,要求平均产量不低于1600千克/亩,
∴2000﹣50(t﹣20)≥1600,
解得t≤28,
∵y=﹣t2+30t﹣360=﹣(t﹣25)2+15,
∴当t=25时,y取最大值15,
而25<28,
∴这批蔬菜可提前15天上市,即这批蔬菜能在5月1日上市.
21.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y件,销售该商品的每天利润为w元.
(1)第x(1≤x≤30)天的销售价为每件 (40+x) 元,这段时间每天的销售量y(件)与x(天)的函数关系式为 y=120﹣2x ;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
解:(1)根据题意得:第x(1≤x≤30)天的销售价为每件(40+x)元,
这段时间每天的销售量y(件)与x(天)的函数关系式为y=120﹣2x,
故答案为:(40+x),y=120﹣2x;
(2)根据题意得:w=(40+x﹣30)(120﹣2x)=﹣2(x﹣25)2+2450,
∵﹣2<0,
∴x=25时,w取最大值2450,
答:从4月1日起,销售该商品第25天时,当天销售利润最大,最大利润2450元;
(3)∵从5月1日起到5月30日当天,销售量一直持续每天比前一天减少2件,
∴当1≤x≤60时,y=120﹣2x,
①当1≤x≤30时,由﹣2(x﹣25)2+2450=2000得:x1=10,x2=40,
∴当10≤x≤30时,每天销售利润不低于2000元,共21天;
②当31≤x≤60时,由(70﹣30)×(120﹣2x)≥2000得:x≤35,
∴当31≤x≤35时,每天销售利润不低于2000元,共5天;
综上所述,该商品在销售过程中,共有26天,每天销售利润不低于2000元.
22.某校开展助力贫困儿童的爱心义卖活动,七(1)班班委组织了33名同学制作甲、乙两种作品,其中每人可制作1件甲作品或2件乙作品.已知制作4件甲作品,每件甲作品可获利20元;当甲作品每多制作一件时,平均每件获利减少0.5元(甲作品制作不少于4件);乙作品每件可获利5元.设安排x人生产甲作品.
(1)完成下列表格(用含x的代数式表示):
作品种类 人数(人) 制作量(件) 每件产品可获利润(元)
甲 x x ﹣0.5x+22
乙 33﹣x ﹣2x+66 5
(2)若制作甲作品可获得的总利润比制作乙作品可获得的总利润多20元,求制作甲作品的人数;
(3)在不改变总人数的情况下,增加制作丙作品,每人可制作1件丙作品(每位同学只制作一种类型的作品),已知丙作品每件可获利13元.若制作乙、丙作品的件数相等,则制作丙作品的同学有 (﹣x+22) 人(用含x的代数式表示),当全部作品都卖完时,总利润的最大值为 445.5 元(直接写出答案).
解:(1)甲作品制作量是x件,每件产品可获利润20﹣0.5(x﹣4)=(﹣0.5x+22)元,
制作乙作品人数是(33﹣x)人,制作乙作品2(33﹣x)=(﹣2x+66)件,
故答案为:x,﹣0.5x+22,33﹣x,﹣2x+66;
(2)根据题意得:x(﹣0.5x+22)﹣5(﹣2x+66)=20,
解得x=50(大于33,不符合题意,舍去)或x=14,
答:制作甲作品的人数是14人;
(3)∵制作乙、丙作品的件数相等,每人可制作2件乙作品,制作1件丙作品,
∴制作丙作品的同学有×(33﹣x)=(﹣x+22)个,
设全部作品都卖完,总利润是y元,
根据题意得:y=x(﹣0.5x+22)+5×(33﹣x)×2+13×(﹣x+22)=﹣0.5(x﹣10)2+446,
∵﹣0.5<0,对称轴为直线x=10,且33﹣x是3的倍数,
∴x=9时,y取最大值﹣0.5×(9﹣10)2+446=445.5,
∴当全部作品都卖完时,总利润的最大值为445.5元,
故答案为:(﹣x+22),445.5.
23.“贵妃芒”芒果品种是广受各地消费者青睐的优质新品种,在我国海南省广泛种植,某水果商以每斤15元的价格从该省批发“贵妃芒”,再按每斤25元价格到市区销售,平均每天可售出60斤,经过调查发现,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.设“贵妃芒”每斤的价格降低x元.
(1)则每天的销售量是 (60+10x) 斤(用含x的代数式表示);
(2)水果商销售“贵妃芒”每天盈利630元,每斤“贵妃芒”的售价应降至每斤多少元?(其他成本忽略不计)
(3)若x的范围为1≤x≤9的正整数,请直接写出水果商的最高利润与最低利润的差为 490 元.
解:(1)∵按每斤25元价格到市区销售,平均每天可售出60斤,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,
∴将“贵妃芒”每斤的价格降低x元,则每天的销售量为(60+10x)斤.
故答案为:(60+10x);
(2)依题意得:(25﹣x﹣15)(60+10x)=630,
整理得:x2﹣4x+3=0,
解得:x1=1,x2=3,
又∵为了尽快减少库存,
∴x=3,
∴25﹣x=22.
答:每斤“贵妃芒”的售价应降至22元;
(3)设水果商每天获得的利润为y元,
根据题意得:y=(25﹣x﹣15)(60+10x)=﹣10x2+40x+600=﹣10(x﹣2)2+640,
∵1≤x≤9,﹣10<0,
∴当x=2时,y有最大值,最大值为640,
当x=9时,y有最小值,最小值为﹣10(9﹣2)2+640=150,
∴水果商的最高利润与最低利润的差为640﹣150=490(元).
故答案为:490.
24.浙江省温州市是全国旅游胜地,2020年受新冠疫情的影响,来温的外来游客在逐年下降.某景区外来游客人数从2019年的2.25万下降到2021年的1.44万.
(1)求2019年到2021年该景区外来游客人数平均每年降低的百分率;
(2)该景区要建一个游乐场(如图所示),其中AD、CD分别靠现有墙DM、DN(墙DM长为27米,墙DN足够长),其余用篱笆围成.篱笆DE将游乐场隔成等腰直角△CED和长方形ADEB两部分,并在三处各留2米宽的大门.已知篱笆总长为54米.
①当AB多长时,游乐场的面积为320平方米?
②当AB= 12 米时,游乐场的面积达到最大,最大为 360 平方米.
解:(1)设2019年到2021年该景区外来游客人数平均每年降低的百分率x,
依题意得:2.25(1﹣x)2=1.44,
解得:x1=0.2=20%,x2=(不合题意,舍去),
答:2019年到2021年该景区外来游客人数平均每年降低的百分率为20%;
(2)设AB=x米,
∵四边形ABED是矩形,
∴AB=DE,∠ADE=∠DEC=90°,
∵△CED是等腰直角三角形,
∴∠EDC=∠DCE=45°,
∴CE=DE=(x﹣2)米,
∴BE=[54﹣x﹣2(x﹣2)+2]米=(60﹣3x)米,
①根据题意得:x(60﹣3x)+x2=320,
解得x1=8,x2=16,
∵60﹣3x≤20,
∴11≤x≤20,
∴x=16,
答:当AB为16米时,游乐场的面积为320平方米;
②设面积为y平方米,
根据题意得:y=x(60﹣3x)+x2=﹣x2+60x=﹣(x﹣12)2+360,
∵60﹣3x<20,
∴11≤x<20,
∴当x=12时,y有最大值,最大值为360.
故答案为:12,360.
25.2022年中秋节,某超市销售一种月饼,成本每千克40元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 55 60
销售量y(千克) 100 90 80
(1)求y与x之间的函数关系式;
(2)物价局规定这种月饼售价每千克不高于65元.设这种月饼每天的利润为W(元),求W与x之间的函数关系式,并求出当售价为多少元时获得最大利润,最大利润是多少?
解:(1)设y=kx+b,
将(50,100)、(60,80)代入,
得:,
解得:,
∴y=﹣2x+200;
(2)W=(x﹣40)(﹣2x+200)=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800,
∵40≤x≤65,
∴当x=65时,W取得最大值为1750,
答:售价为65元时获得最大利润,最大利润是1750元.
26.一商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x (元/件) (x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 4 5 6
y(件) 1000 950 900
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件,求这一周市商场销售这种商品获得的最大利润和售价分别为多少元?
解:(1)设y和x的函数表达式为y=kx+b,
则,
解得,
故y和x的函数表达式为y=﹣50x+1200;
(2)设这一周该商场销售这种商品的利润为w元,
则w=y(x﹣3)=(﹣50x+1200)(x﹣3)=﹣50(x﹣)2+,
∵﹣50<0,x为正整数,
∴当x=13或14时,w有最大值,最大值为5500,
答:一周该商场销售这种商品获得的最大利润为5500元,销售单价分别为13或14元.
二次函数的实际应用解答题专项练习
1.北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民喜爱.某特许零售店“冰墩墩的销售日益火爆.每个纪念品进价40元,规定销售单价不低于48元,且不高于56.5元.销售期间发现,当销售单价定为48元时,每天可售230个,销售单价每上涨1元,每天销量减少10个.现商家提价销售,设每天销售量为y个,销售单价为x元.
(1)填空:y与x之间的函数关系式是 ;自变量x的取值范围是 .
(2)将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?
2.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
3.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x(元),月销售利润为y(元),求y与x的函数关系式;
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)销售单价定为多少时,月销售利润最大?利润最大值为多少?
4.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克.
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足y=﹣10x+840,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
5.大鹏童装店销售某款童装每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖出10件,已知该款童装每件成本30元,设该款童装每件售价x元每星期销售量为y件.
(1)求y与x之间的函数关系式;
(2)若商店按每件售价不超过45元来销售,当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该童装多少件?
6.在运动会比赛时,九年级的一名男同学推铅球,已知铅球经过的路线是某二次函数图象的一部分(如图所示),如果这名男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5).
(1)求出这个二次函数的解析式;
(2)请求出这名男同学比赛时的成绩?
7.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.中国18岁小将苏翊鸣获得冠军.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
这是苏翊鸣参赛前进行的一次训练.
(1)训练时,苏翊鸣的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出苏翊鸣竖直高度的最大值,并求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)训练时,苏翊鸣的着陆点的竖直高度为7米,求着陆点的水平距离为多少?
8.如图,交易会上主办方利用足够长的一段围墙,用围栏围成一个长方形的空地,中间用围栏分割出2个小长方形展厅,并且在与墙平行的一边上各开了一扇宽为1.5m的门,总共用去围栏36m.
(1)若长方形展厅ABCD的面积为90m2,求边AB的长为多少米?
(2)当边AB的长为多少米时,长方形展厅ABCD的面积最大?
9.如图,小区中央公园要修建一个圆形的喷水池,在水池中央垂直于地面安装一个柱子OA,O恰好在水面的中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计水流在离OA距离为1米处达到距水面的最大高度2.25米.
(1)求抛物线的解析式;
(2)若不计其他因素,则水池的半径至少要多少米才能使喷出的水流不至于落到池外?
10.某游乐场的圆形喷水池中心O有一喷水管OA,从点A四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+2.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
(3)现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?
11.如图,有一座抛物线形状的拱桥,对拱桥在水面以上的部分进行测量,得到桥洞的跨度为12米,并且以桥洞拱顶为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系,把测量得到的数据记入表:
x(米) ﹣6 ﹣4 ﹣2 0 2 4 6
y(米) ﹣3.02 ﹣1.33 ﹣0.31 0 ﹣0.32 ﹣1.33 ﹣2.99
(1)请在下面的坐标系中根据已知数据描点,并用平滑的曲线连接;
(2)请结合图象,写出拱桥的桥洞在拱顶下方1米的位置宽度是 米(结果精确到0.1);
(3)现有一艘宽4米,高2米的游船要穿过拱桥的桥洞.为保证安全,要求船顶到竖直方向上拱桥桥洞对应点的距离不小于0.5米,那么这艘船 (填“能”或者“不能”)安全通过.
12.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,如图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系,已知滑道对应的函数为y=x2﹣4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为1米,经实验表明:h=6t2,l=vt.
(1)求滑道对应的函数表达式;
(2)当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;
(3)在试跳中,运动员从A处飞出,运动员甲飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d1,运动员乙飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d2,则d1 d2,(填“>”“=”或“<”).
13.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
14.学校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.5米用5根立柱加固,拱高OC为米.
(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2对应的函数表达式;
(2)请计算一段棚栏所需5很立柱的总长度L.
15.某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为6元/kg,每日销售y/(kg)与销售单价x(元/kg)满足关系式:y=kx+b,部分数据如表:
销售单价x(元/kg) 1 2 … 10
每日销售量(kg) 4900 4800 … 4000
经销售发现,销售单价不低于成本价格且不高于30元/kg.设该食品公司销售这种瓜子的日获利为w(元).
(1)y与x的函数关系式是 ,x的范围是 ;w与x的函数关系式是 ;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司可收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,直接写出a的值.
16.大同南城墙永泰门广场的音乐喷泉,因为有古城墙做背景,成为古都大同美丽特别的风景.如图是其中一个喷泉的示意图,喷泉有一个竖直的喷水枪AB,喷水口为A,喷出水流的运动路线是抛物线,如果水流的最高点P到AB所在直线的距离为1m,且到地面的距离为3.6m,水流的落地点C到喷水枪底部B的距离为2.5m,喷水枪AB应为多长?请你在以BC所在直线为x轴,AB所在直线为y轴的平面直角坐标系中解决问题.
17.据统计,某景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:
购票方式 甲 乙 丙
可游玩景点 A B A和B
门票价格 100元/人 80元/人 160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
18.云南某星级酒店共有50个房间供给受疫情影响需要隔离的人员居住,每间房价不低于200元且不超过350元,酒店还需对隔离人员居住的每个房间每天支出各种费用共计120元已知需要隔离的人员居住的房间数y(单位:间)和每个房间定价x(单位:元)符合一次函数关系,如图是y关于x的函数图象.
(1)求y与x之间的函数解析式;
(2)当房价定为多少元时,酒店利润最大?最大利润是多少元?
19.某商场销售一种季节性产品,以下是该产品在销售期(30天)内的部分信息:
①第x天(x为整数)的销量为(40+2x)千克;
②该产品前10天的售价都是50元千克,从第11天开始售价y(元/千克)是第x天的一次函数,对应关系如表:
第x天 15 20
售价y(元/千克) 45 40
(1)当11≤x≤30时,求出y与x的关系式;
(2)当x为何值时日销售额w最大,最大为多少?
20.今年某市疫情形势严峻,物资紧缺.为保障物资供应,相关部门加强蔬菜抢种和抢收力度,建议取消蔬菜采收后养地的传统做法,采用采收后立即播种的新种植方式.当季某种蔬菜的适宜生育温度为15℃﹣30℃,在平均温度20℃时,传统种植方式平均产量为2500千克/亩,采用新种植方式后,平均产量为a千克/亩.已知A公司在郊区承包该种蔬菜种植面积50亩,其中30亩采用新种植方式,这50亩共采收蔬菜110000千克.
(1)平均温度20℃时,求该种蔬菜采用新种植方式每亩的平均产量;
(2)采用新种植方式的蔬菜原计划在5月15日上市,为提前上市应对需求的激增,A公司启动大棚内智能化控温设备,缩短蔬菜生长周期.经调查,当平均温度超过20℃时,温度升高会导致蔬菜幼苗成活率下降,每升高1℃,平均每亩产量减少50千克;提前上市的天数y(天)与温度t(℃)满足y=﹣t2+30t﹣360(20≤t≤30).为了确保蔬菜所需的供应量,要求平均产量不低于1600千克/亩,判断这批蔬菜能否在5月1日上市?并说明理由.
21.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y件,销售该商品的每天利润为w元.
(1)第x(1≤x≤30)天的销售价为每件 元,这段时间每天的销售量y(件)与x(天)的函数关系式为 ;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
22.某校开展助力贫困儿童的爱心义卖活动,七(1)班班委组织了33名同学制作甲、乙两种作品,其中每人可制作1件甲作品或2件乙作品.已知制作4件甲作品,每件甲作品可获利20元;当甲作品每多制作一件时,平均每件获利减少0.5元(甲作品制作不少于4件);乙作品每件可获利5元.设安排x人生产甲作品.
(1)完成下列表格(用含x的代数式表示):
作品种类 人数(人) 制作量(件) 每件产品可获利润(元)
甲 x
乙 5
(2)若制作甲作品可获得的总利润比制作乙作品可获得的总利润多20元,求制作甲作品的人数;
(3)在不改变总人数的情况下,增加制作丙作品,每人可制作1件丙作品(每位同学只制作一种类型的作品),已知丙作品每件可获利13元.若制作乙、丙作品的件数相等,则制作丙作品的同学有 人(用含x的代数式表示),当全部作品都卖完时,总利润的最大值为 元(直接写出答案).
23.“贵妃芒”芒果品种是广受各地消费者青睐的优质新品种,在我国海南省广泛种植,某水果商以每斤15元的价格从该省批发“贵妃芒”,再按每斤25元价格到市区销售,平均每天可售出60斤,经过调查发现,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.设“贵妃芒”每斤的价格降低x元.
(1)则每天的销售量是 斤(用含x的代数式表示);
(2)水果商销售“贵妃芒”每天盈利630元,每斤“贵妃芒”的售价应降至每斤多少元?(其他成本忽略不计)
(3)若x的范围为1≤x≤9的正整数,请直接写出水果商的最高利润与最低利润的差为 元.
24.浙江省温州市是全国旅游胜地,2020年受新冠疫情的影响,来温的外来游客在逐年下降.某景区外来游客人数从2019年的2.25万下降到2021年的1.44万.
(1)求2019年到2021年该景区外来游客人数平均每年降低的百分率;
(2)该景区要建一个游乐场(如图所示),其中AD、CD分别靠现有墙DM、DN(墙DM长为27米,墙DN足够长),其余用篱笆围成.篱笆DE将游乐场隔成等腰直角△CED和长方形ADEB两部分,并在三处各留2米宽的大门.已知篱笆总长为54米.
①当AB多长时,游乐场的面积为320平方米?
②当AB= 米时,游乐场的面积达到最大,最大为 平方米.
25.2022年中秋节,某超市销售一种月饼,成本每千克40元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 55 60
销售量y(千克) 100 90 80
(1)求y与x之间的函数关系式;
(2)物价局规定这种月饼售价每千克不高于65元.设这种月饼每天的利润为W(元),求W与x之间的函数关系式,并求出当售价为多少元时获得最大利润,最大利润是多少?
26.一商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x (元/件) (x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 4 5 6
y(件) 1000 950 900
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件,求这一周市商场销售这种商品获得的最大利润和售价分别为多少元?
答 案
1.北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民喜爱.某特许零售店“冰墩墩的销售日益火爆.每个纪念品进价40元,规定销售单价不低于48元,且不高于56.5元.销售期间发现,当销售单价定为48元时,每天可售230个,销售单价每上涨1元,每天销量减少10个.现商家提价销售,设每天销售量为y个,销售单价为x元.
(1)填空:y与x之间的函数关系式是 y=﹣10x+710 ;自变量x的取值范围是 48≤x≤56.5 .
(2)将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?
解:(1)根据题意得:y=230﹣10(x﹣48)=﹣10x+710,
∴y与x之间的函数关系式为y=﹣10x+710(48≤x≤56.5);
故答案为:y=﹣10x+710;48≤x≤56.5;
(2)根据题意得:w=(﹣10x+710)(x﹣40)=﹣10x2+1110x﹣28400=﹣10(x﹣55.5)2+2402.5,
∵﹣10<0,
∴当x<55.5时,w随x的增大而增大,
∵48≤x≤56.5,
∴当x=55.5时,w有最大值,最大值为2402.5,
∴将纪念品的销售单价定为55.5元时,商家每天销售纪念品获得的利润w元最大,最大利润是2402.5元.
2.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
解:(1)根据题意得,y=60﹣2x;
(2)设茶商每天的利润为w元,根据题意得,w=(20+x)(﹣2x+60)=﹣2(x﹣5)2+1250,
∵a=﹣2<0,
∴当x=5时,w最大=1250元,
答:该茶商每天的最大利润为1250元.
3.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x(元),月销售利润为y(元),求y与x的函数关系式;
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)销售单价定为多少时,月销售利润最大?利润最大值为多少?
解:(1)由题意可得:
y=(x﹣40)[500﹣(x﹣50)×10]=﹣10x2+1400x﹣40000,
答:y与x的函数关系式是:y=﹣10x2+1400x﹣40000;
(2)将y=8000代入y=﹣10x2+1400x﹣40000,得,
﹣10x2+1400x﹣40000=8000,
解得,x=60或x=80,
又∵40×[500﹣(x﹣50)×10]≤10000,
解得:x≥75,
∴定价为每千克80元,
答:在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为80元;
(3)∵y=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∴当x=70时,月销售利润最大,最大利润是9000,
答:销售单价定为每千克70元时,月销售利润达到最大为9000.
4.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克.
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足y=﹣10x+840,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
解:(1)设现在实际购进这种牛肉每千克a元,则原来购进这种牛肉每千克(a+2)元,
由题意得:32(a+2)=33a,
解得:a=64(元),
答:现在实际购进这种牛肉每千克64元;
(2)设销售利润为w元,由题意得
w=(x﹣64)y=(x﹣64)(﹣10x+840)=﹣10x2+1480x﹣53760=﹣10(x﹣74)2+1000,
所以当x=74时,w有最大值1000.
答:将这种牛肉的销售单价定为74元时,能获得最大利润,最大利润是1000元.
5.大鹏童装店销售某款童装每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖出10件,已知该款童装每件成本30元,设该款童装每件售价x元每星期销售量为y件.
(1)求y与x之间的函数关系式;
(2)若商店按每件售价不超过45元来销售,当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该童装多少件?
解:(1)y=100+10(60﹣x)=﹣10x+700;
(2)设每星期利润为W元,
W=(x﹣30)(﹣10x+700)=﹣10(x﹣50)2+4000,
当x≤45时,W随x的增大而增大,
∴x=545时,W最大值=﹣10×(45﹣50)2+4000=3750,
当每件售价为45元时,每星期的销售利润最大,最大利润3750元;
(3)①由题意:﹣10(x﹣50)2+4000=3910,
解得:x=53或47,
∴当每件童装售价定为53元或47元时,该店一星期可获得3910元的利润.
②由题意:﹣10(x﹣50)2+4000≥3910,
解得:47≤x≤53,
∵y=100+10(60﹣x)=﹣10x+700.
170≤y≤230,
∴每星期至少要销售该款童装170件.
6.在运动会比赛时,九年级的一名男同学推铅球,已知铅球经过的路线是某二次函数图象的一部分(如图所示),如果这名男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5).
(1)求出这个二次函数的解析式;
(2)请求出这名男同学比赛时的成绩?
解:(1)设二次函数的解析式为y=a(x﹣h)2+k,
由于顶点坐标为(6,5),
∴y=a(x﹣6)2+5.
又A(0,2)在抛物线上,
∴2=62 a+5,
解得:a=﹣.
∴二次函数的解析式为y=﹣(x﹣6)2+5,
整理得:y=﹣x2+x+2.
∴这个二次函数的解析式是y=﹣x2+x+2;
(2)当y=0时,﹣x2+x+2=0.
∴x1=6+2,x2=6﹣2(不合题意,舍去).
答:这名男同学比赛时的成绩是(6+2)米.
7.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.中国18岁小将苏翊鸣获得冠军.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
这是苏翊鸣参赛前进行的一次训练.
(1)训练时,苏翊鸣的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出苏翊鸣竖直高度的最大值,并求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)训练时,苏翊鸣的着陆点的竖直高度为7米,求着陆点的水平距离为多少?
解:(1)根据表格中的数据可知,抛物线的顶点坐标为:(8,23.20),
∴h=8,k=23.20,
即该运动员竖直高度的最大值为23.20m,
根据表格中的数据可知,当x=0时,y=20.00,代入y=a(x﹣8)2+23.20得:
20.00=a(0﹣8)2+23.20,
解得:a=﹣0.05,
∴函数关系式为:y=﹣0.05(x﹣8)2+23.20;
(2)把y=7代入y=﹣0.05(x﹣8)2+23.20,
解得:x=26或x=﹣18(不符合题意舍去),
∴着落点的水平距离为26米.
8.如图,交易会上主办方利用足够长的一段围墙,用围栏围成一个长方形的空地,中间用围栏分割出2个小长方形展厅,并且在与墙平行的一边上各开了一扇宽为1.5m的门,总共用去围栏36m.
(1)若长方形展厅ABCD的面积为90m2,求边AB的长为多少米?
(2)当边AB的长为多少米时,长方形展厅ABCD的面积最大?
解:(1)设AB的长为x米,
则BC=36﹣3x+2×1.5=(39﹣3x)米,
根据题意得(39﹣3x)x=90,
解得x1=3,x2=10,
答:AB的长为3或10米;
(2)∵长方形展厅ABCD的面积=(39﹣3x)x=﹣3x2+39x=﹣3(x﹣)2+,
对称轴为x=,
∴当米时,所围成的长方形展厅ABCD的面积最大.
9.如图,小区中央公园要修建一个圆形的喷水池,在水池中央垂直于地面安装一个柱子OA,O恰好在水面的中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计水流在离OA距离为1米处达到距水面的最大高度2.25米.
(1)求抛物线的解析式;
(2)若不计其他因素,则水池的半径至少要多少米才能使喷出的水流不至于落到池外?
解:(1)∵顶点为(1,2.25),
∴设解析式为y=a(x﹣1)2+2.25,
∵函数过点(0,1.25),
∴代入解析式解得a=﹣1,
∴解析式为:y=﹣(x﹣1)2+2.25;
(2)由(1)可知:y=﹣(x﹣1)2+2.25,
令y=0,则﹣(x﹣1)2+2.25=0,
解得x=2.5或x=﹣0.5(舍去),
所以花坛的半径至少为2.5m才能使喷出的水流不至于落到池外.
10.某游乐场的圆形喷水池中心O有一喷水管OA,从点A四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+2.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
(3)现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?
解:(1)当x=0时,y=﹣×(0﹣3)2+2=,
∴点A的坐标为(0,),
∴喷水管高OA高m.
(2)解法一:对于y=﹣(x﹣3)2+2,
令x=4,则y=﹣(4﹣3)2+2=>1.7,
∴小明不会被水喷到;
解法二:令y=1.7,
则﹣(x﹣3)2+2=1.7,
解得:x1=3+,x2=3﹣,
∵3+>4,3﹣<4,
∴小明不会被水喷到;
(3)设喷水管OA的高度要升高hm,
则抛物线的表达式为y=﹣(x﹣3)2+2+h.
把(7,0)代入得:0=﹣(x﹣3)2+2+h,
解得:h=,
∴喷水管OA的高度要升高m.
11.如图,有一座抛物线形状的拱桥,对拱桥在水面以上的部分进行测量,得到桥洞的跨度为12米,并且以桥洞拱顶为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系,把测量得到的数据记入表:
x(米) ﹣6 ﹣4 ﹣2 0 2 4 6
y(米) ﹣3.02 ﹣1.33 ﹣0.31 0 ﹣0.32 ﹣1.33 ﹣2.99
(1)请在下面的坐标系中根据已知数据描点,并用平滑的曲线连接;
(2)请结合图象,写出拱桥的桥洞在拱顶下方1米的位置宽度是 6.8 米(结果精确到0.1);
(3)现有一艘宽4米,高2米的游船要穿过拱桥的桥洞.为保证安全,要求船顶到竖直方向上拱桥桥洞对应点的距离不小于0.5米,那么这艘船 能 (填“能”或者“不能”)安全通过.
解:(1)用描点法作图如下:
(2)由图象可得,拱桥的桥洞在拱顶下方1米的位置宽度是6.8米;
(3)由表中数据知当x=±2时,y=﹣0.32,
当x=±6时,y=﹣2.99,
﹣0.32﹣(﹣2.99)=﹣0.32+2.99=2.67,
∵2.67﹣2=0.67>2,
∴这艘船能安全通过.
故答案为:能.
12.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,如图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系,已知滑道对应的函数为y=x2﹣4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为1米,经实验表明:h=6t2,l=vt.
(1)求滑道对应的函数表达式;
(2)当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;
(3)在试跳中,运动员从A处飞出,运动员甲飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d1,运动员乙飞出的路径近似看做函数y=﹣x2+x+图象的一部分,着陆时水平距离为d2,则d1 < d2,(填“>”“=”或“<”).
解:(1)由题意得:A(1,18),
把A(1,18)代入解析式得:×12﹣4×1+c=18,
解得:c=21.8,
∴滑道对应的函数表达式为y=x2﹣4x+21.8;
(2)当v=5,t=1时,h=6t2=6,l=vt=5,
当x=6时,y=×62﹣4×6+21.8=5,
而18﹣h=18﹣6=12>5,
∴运动员此时未落在滑道上;
(3)对于y=﹣x2+x+,
令y=0,则﹣x2+x+=0,
解得x=1±3,
∴d1=1+3;
对于y=﹣x2+x+,
令y=0,则﹣x2+x+=0,
解得x=1+6,
∴d2=1+6,
∵d1=1+,d2=1+,
∴d1<d2.
故答案为:<.
13.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
解:(1)A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元,
根据题意得,,
解得,
答:A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元;
(2)设B品牌粽子每袋的销售价降低a元时,每天售出B品牌粽子所获得的利润最大,利润为w元,
根据题意得,w=(54﹣a﹣30)(20+5a)=﹣5a2+100a+480=﹣5(a﹣10)2+980,
∵﹣5<0,
∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980元.
14.学校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.5米用5根立柱加固,拱高OC为米.
(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2对应的函数表达式;
(2)请计算一段棚栏所需5很立柱的总长度L.
解:(1)由已知:OC=米,AC=1.5,
得点A的坐标为(1.5,),
代入y=ax2,
得a=,
∴抛物线的解析式为y=x2;
(2)点C1,C2的横坐标分别为0.5,1,
代入y=x2,
得点C1,C2的纵坐标分别为:
y1=×0.52=0.2,y2=×12=0.8,
∴立柱C1D1=﹣0.2=1.6,C2D2=﹣0.8=1,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:2(C1D1+C2D2)+OC=2(1.6+1)+1.8=7(米).
15.某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为6元/kg,每日销售y/(kg)与销售单价x(元/kg)满足关系式:y=kx+b,部分数据如表:
销售单价x(元/kg) 1 2 … 10
每日销售量(kg) 4900 4800 … 4000
经销售发现,销售单价不低于成本价格且不高于30元/kg.设该食品公司销售这种瓜子的日获利为w(元).
(1)y与x的函数关系式是 y=﹣100x+5000 ,x的范围是 x>1 ;w与x的函数关系式是 w=﹣100x2+5600x﹣32000(6≤x≤30) ;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司可收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,直接写出a的值.
解:(1)由表中数据可得,当x=1时,y=4900,当x=2时,y=4800,代入y=kx+b得,
,
解得,
∴y与x的函数关系式是y=﹣100x+5000,且x>1;
由于销售单价不低于成本价格(6元>且不高于30元/kg,
则w=(x﹣6)(﹣100x+5000)﹣2000
=﹣100x2+5600x﹣32000(6≤x≤30).
故答案为:y=﹣100x+5000;x>1;w=﹣100x2+5600x﹣32000(6≤x≤30).
(2)由(1)知,w=﹣100x2+5600x﹣32000(6≤x≤30).
∵a=﹣100<0,
∴函数图象开口向下,有最大值,
函数图象的对称轴为x=﹣=28,
∵6≤x≤30,
∴当x=28时,函数w有最大值,为46400,
∴销售单价定位28元时,获利最大,为46400元;
(3)收取α元后,利润为w=(x﹣6﹣a)(﹣100x+5000)﹣2000=﹣100x2+(5600+100a)x﹣32000﹣5000a,
∵a=﹣100<0,
∴函数图象开口向下,有最大值,
又函数图象的对称轴为x=﹣=28+a,
∵a<4,
∴当x=28+a时,获利最大值为42100元,
将x=28+a代入得,(28+a﹣6﹣a)[﹣100(28+a)+5000]﹣2000=42100,
解得a=2或a=6(舍),
∴a=2.
16.大同南城墙永泰门广场的音乐喷泉,因为有古城墙做背景,成为古都大同美丽特别的风景.如图是其中一个喷泉的示意图,喷泉有一个竖直的喷水枪AB,喷水口为A,喷出水流的运动路线是抛物线,如果水流的最高点P到AB所在直线的距离为1m,且到地面的距离为3.6m,水流的落地点C到喷水枪底部B的距离为2.5m,喷水枪AB应为多长?请你在以BC所在直线为x轴,AB所在直线为y轴的平面直角坐标系中解决问题.
解:如图:
由题意知,抛物线的顶点P的坐标为(1,3.6)、点C(2.5,0),
设抛物线的解析式为y=a(x﹣1)2+3.6,
将点C(2.5,0)代入,得:2.25a+3.6=0,
解得:a=﹣1.6,
则抛物线的解析式为y=﹣1.6(x﹣1)2+3.6;
当x=0时,有y=﹣1.6(0﹣1)2+3.6=2,
∴AB=2,
答:喷水枪AB应为2m.
17.据统计,某景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:
购票方式 甲 乙 丙
可游玩景点 A B A和B
门票价格 100元/人 80元/人 160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
解:①由题意得:
100×(2﹣10×0.06)+80×(3﹣10×0.04)+(160﹣10)×(2+10×0.06+10×0.04)=798(万元).
答:景区六月份的门票总收入为798万元;
②设丙种门票价格降低x元,景区六月份的门票总收入为W万元,
由题意,得
W=100(2﹣0.06x)+80(3﹣0.04x)+(160﹣x)(2+0.06x+0.04x),
化简,得W=﹣0.1(x﹣24)2+817.6,
∵﹣0.1<0,
∴当x=24时,W取最大值,为817.6万元.
答:当丙种门票价格下降24元时,景区六月份的门票总收入有最大值,最大值是817.6万元.
18.云南某星级酒店共有50个房间供给受疫情影响需要隔离的人员居住,每间房价不低于200元且不超过350元,酒店还需对隔离人员居住的每个房间每天支出各种费用共计120元已知需要隔离的人员居住的房间数y(单位:间)和每个房间定价x(单位:元)符合一次函数关系,如图是y关于x的函数图象.
(1)求y与x之间的函数解析式;
(2)当房价定为多少元时,酒店利润最大?最大利润是多少元?
解:(1)由题意,设y关于x的函数解析式为y=kx+b,
把(280,40),(290,38)代入得:
,
解得:,
∴y与x之间的函数解析式为y=﹣x+96(230≤x≤350);
(2)设酒店的利润为w元,
则w=(x﹣120)y=(x﹣120)(﹣x+96)=﹣x2+120x﹣11520=﹣(x﹣300)2+6480,
∵﹣<0,230≤x≤350
∴当x=300时,w取得最大值,最大值为6480元,
答:当每间房价定价为300元时,酒店每天所获利润最大,最大利润是6480元.
19.某商场销售一种季节性产品,以下是该产品在销售期(30天)内的部分信息:
①第x天(x为整数)的销量为(40+2x)千克;
②该产品前10天的售价都是50元千克,从第11天开始售价y(元/千克)是第x天的一次函数,对应关系如表:
第x天 15 20
售价y(元/千克) 45 40
(1)当11≤x≤30时,求出y与x的关系式;
(2)当x为何值时日销售额w最大,最大为多少?
解:(1)当11≤x≤30时,设y与x的关系式为y=kx+b,
将(15,45),(20,40)代入得:
,
解得,
∴y=﹣x+60(11≤x≤30);
(2)当1≤x≤10时,w=50(40+2x)=100x+2000,
∵100>0,
∴w随x的增大而增大,
∴x=10时,w最大为100×10+2000=3000(元),
当11≤x≤30时,w=(﹣x+60)(40+2x)=﹣2(x﹣20)2+3200,
∵﹣2<0,
∴x=20时,w取最大值3200,
∵3000<3200,
∴x为20时日销售额w最大,最大为3200元.
20.今年某市疫情形势严峻,物资紧缺.为保障物资供应,相关部门加强蔬菜抢种和抢收力度,建议取消蔬菜采收后养地的传统做法,采用采收后立即播种的新种植方式.当季某种蔬菜的适宜生育温度为15℃﹣30℃,在平均温度20℃时,传统种植方式平均产量为2500千克/亩,采用新种植方式后,平均产量为a千克/亩.已知A公司在郊区承包该种蔬菜种植面积50亩,其中30亩采用新种植方式,这50亩共采收蔬菜110000千克.
(1)平均温度20℃时,求该种蔬菜采用新种植方式每亩的平均产量;
(2)采用新种植方式的蔬菜原计划在5月15日上市,为提前上市应对需求的激增,A公司启动大棚内智能化控温设备,缩短蔬菜生长周期.经调查,当平均温度超过20℃时,温度升高会导致蔬菜幼苗成活率下降,每升高1℃,平均每亩产量减少50千克;提前上市的天数y(天)与温度t(℃)满足y=﹣t2+30t﹣360(20≤t≤30).为了确保蔬菜所需的供应量,要求平均产量不低于1600千克/亩,判断这批蔬菜能否在5月1日上市?并说明理由.
解:(1)根据题意得:30a+(50﹣30)×2500=110000,
解得a=2000,
答:平均温度20℃时,该种蔬菜采用新种植方式每亩的平均产量是2000千克;
(2)∵每升高1℃,平均每亩产量减少50千克,要求平均产量不低于1600千克/亩,
∴2000﹣50(t﹣20)≥1600,
解得t≤28,
∵y=﹣t2+30t﹣360=﹣(t﹣25)2+15,
∴当t=25时,y取最大值15,
而25<28,
∴这批蔬菜可提前15天上市,即这批蔬菜能在5月1日上市.
21.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y件,销售该商品的每天利润为w元.
(1)第x(1≤x≤30)天的销售价为每件 (40+x) 元,这段时间每天的销售量y(件)与x(天)的函数关系式为 y=120﹣2x ;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
解:(1)根据题意得:第x(1≤x≤30)天的销售价为每件(40+x)元,
这段时间每天的销售量y(件)与x(天)的函数关系式为y=120﹣2x,
故答案为:(40+x),y=120﹣2x;
(2)根据题意得:w=(40+x﹣30)(120﹣2x)=﹣2(x﹣25)2+2450,
∵﹣2<0,
∴x=25时,w取最大值2450,
答:从4月1日起,销售该商品第25天时,当天销售利润最大,最大利润2450元;
(3)∵从5月1日起到5月30日当天,销售量一直持续每天比前一天减少2件,
∴当1≤x≤60时,y=120﹣2x,
①当1≤x≤30时,由﹣2(x﹣25)2+2450=2000得:x1=10,x2=40,
∴当10≤x≤30时,每天销售利润不低于2000元,共21天;
②当31≤x≤60时,由(70﹣30)×(120﹣2x)≥2000得:x≤35,
∴当31≤x≤35时,每天销售利润不低于2000元,共5天;
综上所述,该商品在销售过程中,共有26天,每天销售利润不低于2000元.
22.某校开展助力贫困儿童的爱心义卖活动,七(1)班班委组织了33名同学制作甲、乙两种作品,其中每人可制作1件甲作品或2件乙作品.已知制作4件甲作品,每件甲作品可获利20元;当甲作品每多制作一件时,平均每件获利减少0.5元(甲作品制作不少于4件);乙作品每件可获利5元.设安排x人生产甲作品.
(1)完成下列表格(用含x的代数式表示):
作品种类 人数(人) 制作量(件) 每件产品可获利润(元)
甲 x x ﹣0.5x+22
乙 33﹣x ﹣2x+66 5
(2)若制作甲作品可获得的总利润比制作乙作品可获得的总利润多20元,求制作甲作品的人数;
(3)在不改变总人数的情况下,增加制作丙作品,每人可制作1件丙作品(每位同学只制作一种类型的作品),已知丙作品每件可获利13元.若制作乙、丙作品的件数相等,则制作丙作品的同学有 (﹣x+22) 人(用含x的代数式表示),当全部作品都卖完时,总利润的最大值为 445.5 元(直接写出答案).
解:(1)甲作品制作量是x件,每件产品可获利润20﹣0.5(x﹣4)=(﹣0.5x+22)元,
制作乙作品人数是(33﹣x)人,制作乙作品2(33﹣x)=(﹣2x+66)件,
故答案为:x,﹣0.5x+22,33﹣x,﹣2x+66;
(2)根据题意得:x(﹣0.5x+22)﹣5(﹣2x+66)=20,
解得x=50(大于33,不符合题意,舍去)或x=14,
答:制作甲作品的人数是14人;
(3)∵制作乙、丙作品的件数相等,每人可制作2件乙作品,制作1件丙作品,
∴制作丙作品的同学有×(33﹣x)=(﹣x+22)个,
设全部作品都卖完,总利润是y元,
根据题意得:y=x(﹣0.5x+22)+5×(33﹣x)×2+13×(﹣x+22)=﹣0.5(x﹣10)2+446,
∵﹣0.5<0,对称轴为直线x=10,且33﹣x是3的倍数,
∴x=9时,y取最大值﹣0.5×(9﹣10)2+446=445.5,
∴当全部作品都卖完时,总利润的最大值为445.5元,
故答案为:(﹣x+22),445.5.
23.“贵妃芒”芒果品种是广受各地消费者青睐的优质新品种,在我国海南省广泛种植,某水果商以每斤15元的价格从该省批发“贵妃芒”,再按每斤25元价格到市区销售,平均每天可售出60斤,经过调查发现,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.设“贵妃芒”每斤的价格降低x元.
(1)则每天的销售量是 (60+10x) 斤(用含x的代数式表示);
(2)水果商销售“贵妃芒”每天盈利630元,每斤“贵妃芒”的售价应降至每斤多少元?(其他成本忽略不计)
(3)若x的范围为1≤x≤9的正整数,请直接写出水果商的最高利润与最低利润的差为 490 元.
解:(1)∵按每斤25元价格到市区销售,平均每天可售出60斤,如果每斤“贵妃芒”的售价每降低1元,那么平均每天的销售量会增加10斤,
∴将“贵妃芒”每斤的价格降低x元,则每天的销售量为(60+10x)斤.
故答案为:(60+10x);
(2)依题意得:(25﹣x﹣15)(60+10x)=630,
整理得:x2﹣4x+3=0,
解得:x1=1,x2=3,
又∵为了尽快减少库存,
∴x=3,
∴25﹣x=22.
答:每斤“贵妃芒”的售价应降至22元;
(3)设水果商每天获得的利润为y元,
根据题意得:y=(25﹣x﹣15)(60+10x)=﹣10x2+40x+600=﹣10(x﹣2)2+640,
∵1≤x≤9,﹣10<0,
∴当x=2时,y有最大值,最大值为640,
当x=9时,y有最小值,最小值为﹣10(9﹣2)2+640=150,
∴水果商的最高利润与最低利润的差为640﹣150=490(元).
故答案为:490.
24.浙江省温州市是全国旅游胜地,2020年受新冠疫情的影响,来温的外来游客在逐年下降.某景区外来游客人数从2019年的2.25万下降到2021年的1.44万.
(1)求2019年到2021年该景区外来游客人数平均每年降低的百分率;
(2)该景区要建一个游乐场(如图所示),其中AD、CD分别靠现有墙DM、DN(墙DM长为27米,墙DN足够长),其余用篱笆围成.篱笆DE将游乐场隔成等腰直角△CED和长方形ADEB两部分,并在三处各留2米宽的大门.已知篱笆总长为54米.
①当AB多长时,游乐场的面积为320平方米?
②当AB= 12 米时,游乐场的面积达到最大,最大为 360 平方米.
解:(1)设2019年到2021年该景区外来游客人数平均每年降低的百分率x,
依题意得:2.25(1﹣x)2=1.44,
解得:x1=0.2=20%,x2=(不合题意,舍去),
答:2019年到2021年该景区外来游客人数平均每年降低的百分率为20%;
(2)设AB=x米,
∵四边形ABED是矩形,
∴AB=DE,∠ADE=∠DEC=90°,
∵△CED是等腰直角三角形,
∴∠EDC=∠DCE=45°,
∴CE=DE=(x﹣2)米,
∴BE=[54﹣x﹣2(x﹣2)+2]米=(60﹣3x)米,
①根据题意得:x(60﹣3x)+x2=320,
解得x1=8,x2=16,
∵60﹣3x≤20,
∴11≤x≤20,
∴x=16,
答:当AB为16米时,游乐场的面积为320平方米;
②设面积为y平方米,
根据题意得:y=x(60﹣3x)+x2=﹣x2+60x=﹣(x﹣12)2+360,
∵60﹣3x<20,
∴11≤x<20,
∴当x=12时,y有最大值,最大值为360.
故答案为:12,360.
25.2022年中秋节,某超市销售一种月饼,成本每千克40元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 55 60
销售量y(千克) 100 90 80
(1)求y与x之间的函数关系式;
(2)物价局规定这种月饼售价每千克不高于65元.设这种月饼每天的利润为W(元),求W与x之间的函数关系式,并求出当售价为多少元时获得最大利润,最大利润是多少?
解:(1)设y=kx+b,
将(50,100)、(60,80)代入,
得:,
解得:,
∴y=﹣2x+200;
(2)W=(x﹣40)(﹣2x+200)=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800,
∵40≤x≤65,
∴当x=65时,W取得最大值为1750,
答:售价为65元时获得最大利润,最大利润是1750元.
26.一商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x (元/件) (x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 4 5 6
y(件) 1000 950 900
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件,求这一周市商场销售这种商品获得的最大利润和售价分别为多少元?
解:(1)设y和x的函数表达式为y=kx+b,
则,
解得,
故y和x的函数表达式为y=﹣50x+1200;
(2)设这一周该商场销售这种商品的利润为w元,
则w=y(x﹣3)=(﹣50x+1200)(x﹣3)=﹣50(x﹣)2+,
∵﹣50<0,x为正整数,
∴当x=13或14时,w有最大值,最大值为5500,
答:一周该商场销售这种商品获得的最大利润为5500元,销售单价分别为13或14元.
同课章节目录
