【专项】二次函数的应用解答题专项练习(含解析)
文档属性
| 名称 | 【专项】二次函数的应用解答题专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 585.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 12:43:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数的应用解答题专项练习
1.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.
2.第二十届省运会于2022年在泰州举行,运动会纪念微章在某网店上进行销售.当每枚售价20元时,平均每天可售出100枚为了扩大销售,现采取了降价措施,在每枚售价不少于15元的前提下,销售一段时间后,发现销售单价每降低I元,平均每天可多售出10枚.若每枚微章降价a(a为正数)元.
(1)降价后平均每天销售数量为 枚(用含a的代数式表示),a的取值范围是 ;
(2)当该网店每天销售额为2210元时,求a的值.
3.如图,二小球从斜坡A点处抛出,正好穿过B点的篮筐,落在斜坡底部的O点,以O为坐标原点建立直角坐标系,B的坐标为(,),斜坡的坡比为1:2,A点距地面的高度为1.5米,球的抛出路线可以用二次函数刻画.
(1)求二次函数的表达式;
(2)求小球到达的最高点的坐标.
4.水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的变化规律符合一次函数关系,部分数据如表:
销售时间t(1≤t≤15,t为整数)(天) 1 4 5 8 12
销售单价p(元/千克) 20.25 21 21.25 22 23
(1)试求p关于t的函数解析式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=﹣2t+120(1≤t≤15,t为整数).求销售过程中最大日销售利润为多少?
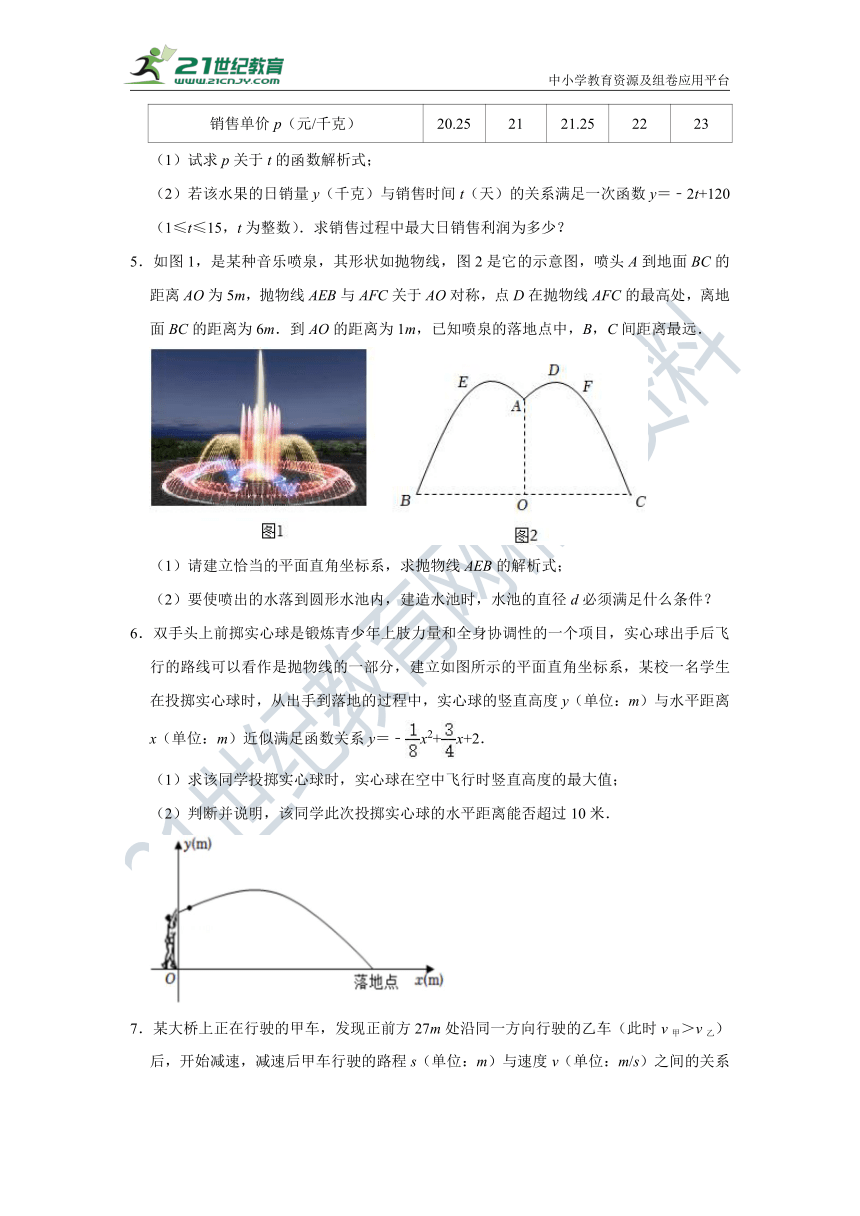
5.如图1,是某种音乐喷泉,其形状如抛物线,图2是它的示意图,喷头A到地面BC的距离AO为5m,抛物线AEB与AFC关于AO对称,点D在抛物线AFC的最高处,离地面BC的距离为6m.到AO的距离为1m,已知喷泉的落地点中,B,C间距离最远.
(1)请建立恰当的平面直角坐标系,求抛物线AEB的解析式;
(2)要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须满足什么条件?
6.双手头上前掷实心球是锻炼青少年上肢力量和全身协调性的一个项目,实心球出手后飞行的路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,某校一名学生在投掷实心球时,从出手到落地的过程中,实心球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣x2+x+2.
(1)求该同学投掷实心球时,实心球在空中飞行时竖直高度的最大值;
(2)判断并说明,该同学此次投掷实心球的水平距离能否超过10米.
7.某大桥上正在行驶的甲车,发现正前方27m处沿同一方向行驶的乙车(此时v甲>v乙)后,开始减速,减速后甲车行驶的路程s(单位:m)与速度v(单位:m/s)之间的关系式为s=﹣v2+128(0≤v≤16);甲车行驶的速度v(单位:m/s)与时间t(单位:s)的关系可以用一次函数表示(如图).
(1)当甲车减速4s时,它行驶的路程是多少?
(2)若乙车以一定的速度一直匀速行驶,经过多长时间两车之间的最近距离是2.5m?(提示:甲车减速后,当甲、乙两车速度相同时,车距最小)
8.某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值.
9.温州某百货商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元(x≥7).
(1)该商品每天的销售量: (用含x的代数式表示);
(2)若该商场当天销售这种商品所获得的利润为480元,求x的值.
(3)当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?此时最大利润为多少?
10.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元
(1)如果销售单价定为25元,那么健身球每天的销售量是 个;
(2)求w与x之间的函数关系式;
(3)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
11.“十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.
(1)若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?
(2)为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?
12.某水果店销售一种新鲜水果,平均每天可售出120箱,每箱盈利60元,为了扩大销售减少库存,水果店决定采取适当的降价措施,经调查发现,每箱水果每降价5元,水果店平均每天可多售出20箱.设每箱水果降价x元.
(1)当x=10时,每箱利润 元,平均每天可售出 箱水果;
(2)设每天销售该水果的总利润为w元.
①求w与x之间的函数解析式;
②试判断w能否达到8200元,如果能达到,求出此时x的值;如果不能达到,求出w的最大值.
13.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
14.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图7所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3m,运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
15.某商品的进价为每件40元,售价为每件50元.每个月可卖出420件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为W元.求每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
16.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
产品 每件售价(万元) 每件成本(万元) 每年其他费用(万元) 每年最大产销量(件)
甲 12 a 40 150
乙 18 8 40+0.05x2 80
其中a为常数,且5≤a≤10.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
17.某商品的成本w(单位:百元)由包装费和生产费两部分组成.其中当原料数量x(单位:千克)低于4千克时,包装费y1(单位:百元)与原料数量x之间的关系式为y1=1.2﹣0.3x;当原料数量不低于4千克时,包装费全免.生产费2(单位:百元)与原料数量x之间的关系式为:y2=ax2+0.1x(a>0).
(1)当原料数量x=3时,该商品的成本为: (百元);当原料数量x=5时,该商品的成本为: (百元);(直接用含a的式子表示)
(2)若a=0.1,求原料数量x为多少千克时,该商品的成本最少?最少是多少百元?
(3)若当原料数量低于4千克时,有且仅有唯一正整数x使得该商品的成本w不高于2百元,直接写出a的取值范围.
18.月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句小饼如嚼月,中有和饴赞美月饼.为满足市场需求,某蛋糕店在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是60元,蛋糕店规定每盒售价不得少于70元,根据以往销售经验发现:当售价定为每盒70元时,每天可卖出500盒,每盒售价每提高1元时,每天要少卖出20盒,请解答下列问题:
(1)若每盒月饼售价提高20元,则每天可卖出 盒,销售利润为 元;
(2)设每天的销售利润为y元,每盒售价提高x元(x为整数),请求出γ与x之间的函数解析式,并直接写出当每盒售价定为多少元时,每天销售的总利润最大?最大利润是多少?
(3)为稳定物价,有关管理部]限定:这种月饼的每盒售价不得高出78元,如果蛋糕店想要每天获得6000元的利润,那么蛋糕店每天销售月饼 盒.
19.一名男生推铅球,其铅球运行的路线如图,是抛物线的一部分.当水平距离x为3米时,铅球的行进高度y达到最高2米.已知推出铅球的初始高度是米.
(1)求铅球运行路线的解析式;
(2)求铅球推出的水平距离OA.
20.某公司的商品进价每件60元,售价每件130元,为了支持“抗新冠肺炎”,每销售一件捐款4元.且未来30天,该商品将开展每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,市场调查发现,设第x天(1≤x≤30且x为整数)的销量为y件,y与x满足一次函数关系,其对应数据如表:
x(天) … 1 3 5 7 …
y(件) … 35 45 55 65 …
(1)直接写出y与x的函数关系式;
(2)设第x天去掉捐款后的利润为W元,试求出W与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
21.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元(x≥100).
(1)每天有游客居住的房间数为 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
22.2022年体育中考,增设了考生进入考点需进行体温检测的要求,防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数y(人)与时间x(分钟)的变化情况,数据如表:
时间x(分钟) 0 1 2 3 4 5 6 7 8 9 9≤x
人数y(人) 0 170 320 450 560 650 720 770 800 810 810
(1)分析前9分钟内考生进入考点的累计人数与时间的变化规律,发现它符合二次函数的模型,你能求出这段时间内y与x之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
23.如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣12)2+h,小明罚任意球时防守队员站在小明正前方9m处组成人墙,防守队员的身高为2.1m,对手球门与小明的水平距离为18m,已知足球球门高为2.43m.假定小明罚出的任意球恰好射正对手球门.
(1)当h=3时,求y与x的关系式;
(2)当h=3时,足球能否越过人墙?足球会不会踢飞?请说明理由;
(3)若小明罚出的任意球一定能直接射进对手球门得分,求h的取值范围.
24.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为x米,与湖面的垂直高度为y米.下面的表中记录了x与y的五组数据:
x(米) 0 1 2 3 4
y(米) 0.5 1.25 1.5 1.25 0.5
(1)在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示y与x函数关系的图象;
(2)求y与x函数表达式;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).
25.某公司生产的某种时令商品每件成本为20元,经过市场调研发现:
①这种商品在未来40天内的日销售量m(件)与时间t(天)的关系为:m=﹣2t+96.
②未来40天内,该商品每天的单价y(元/件)与时间t(天)(t为整数)之间关系的函数图象如图所示.
请结合上述信息解决下列问题:
(1)经计算得,当0<t≤20时,y关于t的函数关系式为 ;则当20<t≤40时,y关于t的函数关系式为 .
(2)请预测未来40天中哪一天的单价是27元?
(3)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
参考答案
1.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.
解:∵h=﹣5t2+20t=﹣5(t﹣2)2+20,
且﹣5<0,
∴当t=2时,h取最大值20,
答:小球飞行高度达到最高时的飞行时间为2s.
2.第二十届省运会于2022年在泰州举行,运动会纪念微章在某网店上进行销售.当每枚售价20元时,平均每天可售出100枚为了扩大销售,现采取了降价措施,在每枚售价不少于15元的前提下,销售一段时间后,发现销售单价每降低I元,平均每天可多售出10枚.若每枚微章降价a(a为正数)元.
(1)降价后平均每天销售数量为 (100+10a) 枚(用含a的代数式表示),a的取值范围是 0<a≤5 ;
(2)当该网店每天销售额为2210元时,求a的值.
解:(1)∵销售单价每降低1元,平均每天可多售出10枚,
∴每枚商品降价a元,平均每天多售出10a枚,
∵降价前平均每天可售出100枚,
∴降价后平均每天可售出(100+10a)枚,
∵每枚售价不少于15元,降价后售价为(20﹣a)元,
∴20﹣a≥15,
解得:0<a≤5,
故答案为:(100+10a),0<a≤5;
(2)由(1)知:(20﹣a)(100+10a)=2210,
整理得:a2﹣10a+21=0,
解得:a1=3,a2=7,
∵a≤5,
∴a=3.
3.如图,二小球从斜坡A点处抛出,正好穿过B点的篮筐,落在斜坡底部的O点,以O为坐标原点建立直角坐标系,B的坐标为(,),斜坡的坡比为1:2,A点距地面的高度为1.5米,球的抛出路线可以用二次函数刻画.
(1)求二次函数的表达式;
(2)求小球到达的最高点的坐标.
解:(1)过A作AD⊥x轴,垂足为D,如图:
∵斜坡的坡比为1:2,
∴AD:OD=1:2,
∵AD=1.5,
∴OD=3,
∴A(3,1.5),
设二次函数的表达式为y=ax2+bx,
将A(3,1.5)、B(,)两点坐标代入得:
,
解得,
∴二次函数的表达式为y=﹣x2+2x;
(2)∵y=﹣x2+2x=﹣(x﹣2)2+2,
且﹣<0,
∴当x=2时,y取最大值2,
∴小球到达的最高点的坐标为(2,2).
4.水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的变化规律符合一次函数关系,部分数据如表:
销售时间t(1≤t≤15,t为整数)(天) 1 4 5 8 12
销售单价p(元/千克) 20.25 21 21.25 22 23
(1)试求p关于t的函数解析式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=﹣2t+120(1≤t≤15,t为整数).求销售过程中最大日销售利润为多少?
解:(1)设p与t之间的变化的一次函数关系为:p=kt+b,
将点(4,21)、(8,22)代入上式得:,
解得:,
故p关于t的函数表达式为:p=t+20(1≤t≤15,t为整数);
(2)设日销售利润为w,
由题意得:w=y(p﹣10)=(﹣2t+120)(t+20﹣10)=﹣(t﹣10)2+1250(1≤t≤15,t为整数),
∵﹣<0,
∴当t=10时,w有最大值,最大值为1250;
答:销售过程中最大日销售利润为1250元.
5.如图1,是某种音乐喷泉,其形状如抛物线,图2是它的示意图,喷头A到地面BC的距离AO为5m,抛物线AEB与AFC关于AO对称,点D在抛物线AFC的最高处,离地面BC的距离为6m.到AO的距离为1m,已知喷泉的落地点中,B,C间距离最远.
(1)请建立恰当的平面直角坐标系,求抛物线AEB的解析式;
(2)要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须满足什么条件?
解:(1)以O为原点,以BC所在直线为x轴,以AO所在直线为y轴建立平面直角坐标系,如图所示:
由题意知,A(0,5),D(1,6),
∵抛物线AEB与AFC关于AO对称,
∴抛物线AEB的顶点坐标为(﹣1,6),
设抛物线AEB的解析式为y=a(x+1)2+6,
把A(0,5)代入解析式得:5=a(0+1)2+6,
解得a=﹣1,
∴抛物线AEB的解析式为y=﹣(x+1)2+6;
(2)令y=0,则﹣(x+1)2+6=0,
解得x1=﹣1+,x2=﹣1﹣(舍去),
∴BC=2OB=﹣2+2.
答:要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须大于﹣2+2.
6.双手头上前掷实心球是锻炼青少年上肢力量和全身协调性的一个项目,实心球出手后飞行的路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,某校一名学生在投掷实心球时,从出手到落地的过程中,实心球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣x2+x+2.
(1)求该同学投掷实心球时,实心球在空中飞行时竖直高度的最大值;
(2)判断并说明,该同学此次投掷实心球的水平距离能否超过10米.
解:(1)y=﹣x2+x+2=﹣(x2﹣6x)+2=﹣(x﹣3)2+,
∵﹣<0,
∴当x=3时,y有最大值,最大值为,
答:实心球在空中飞行时竖直高度的最大值为;
(2)令y=0,则=﹣x2+x+2=0,
解得x1=﹣2,x2=8,
∵8<10,
∴该同学此次投掷实心球的水平距离不能超过10米.
7.某大桥上正在行驶的甲车,发现正前方27m处沿同一方向行驶的乙车(此时v甲>v乙)后,开始减速,减速后甲车行驶的路程s(单位:m)与速度v(单位:m/s)之间的关系式为s=﹣v2+128(0≤v≤16);甲车行驶的速度v(单位:m/s)与时间t(单位:s)的关系可以用一次函数表示(如图).
(1)当甲车减速4s时,它行驶的路程是多少?
(2)若乙车以一定的速度一直匀速行驶,经过多长时间两车之间的最近距离是2.5m?(提示:甲车减速后,当甲、乙两车速度相同时,车距最小)
解:(1)设一次函数表达式为v=kt+b,
∵一次函数经过(3,13),(6,10),
则,
解得,
∴一次函数表达式为v=﹣t+16,
∴当t=4时,速度为12m/s,
∴当v=12时,s=﹣v2+128=﹣m,
∴当甲车减速4s时,它行驶的路程是56m;
(2)当v甲>v乙时,两车之间的距离逐渐变小,当v甲<v乙时,两车之间的距离逐渐变大,
∴当两车速度相等时,两车之间距离最小.
根据题意,得:S甲+2.5=27+S乙,
∴﹣(t﹣16)2+128+2.5=27+(t﹣16)t,
化简,得:t2=49.
∴t1=7,t2=﹣7(舍).
答:经过7s两车相距的最近距离是2.5m.
8.某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值.
解:(1)根据题意得:S=(250﹣200) 10y﹣x=500(﹣0.001x2+0.06x+1)﹣x=﹣x2+29x+500,
∴年利润S(万元)与广告费用x(万元)的函数关系式为S=﹣x2+29x+500;
(2)∵S=﹣(x﹣29)2+920.5(10≤x≤50),
∴当10≤x<29时,S随着x的增大而增大;
当29<x≤50时,S随着x的增大而减小;
当x=29时,S有最大值920.5.
故年利润S的最大值为920.5万元.
9.温州某百货商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元(x≥7).
(1)该商品每天的销售量: (﹣20x+300)元 (用含x的代数式表示);
(2)若该商场当天销售这种商品所获得的利润为480元,求x的值.
(3)当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?此时最大利润为多少?
解:(1)根据题意得,160﹣20(x﹣7)=﹣20x+300,
故答案为:(﹣20x+300)元;
(2)根据题意得,(x﹣5)(﹣20x+300)=480,
解得x=9或11;
(3)设销售的总利润为y元,根据题意得,
y=(x﹣5)(﹣20x+300)=﹣20x2+400x﹣1500=﹣20(x﹣10)2+500,
∴当x=10时,y有最大值为500,
答:当商品的销售单价定为10元时,该商店销售这种商品获得的利润最大,此时最大利润为500元.
10.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元
(1)如果销售单价定为25元,那么健身球每天的销售量是 30 个;
(2)求w与x之间的函数关系式;
(3)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
解:(1)在y=﹣2x+80中,令x=25得:
y=﹣2×25+80=30,
故答案为:30;
(2)根据题意得:w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600,
∴w与x之间的函数关系式为w=﹣2x2+120x﹣1600;
(3)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w取最大值,最大值为200,
答:该种健身球销售单价定为30元时,每天的销售利润最大,最大利润是200元.
11.“十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.
(1)若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?
(2)为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?
解:(1)设该花卉每盆售价是x元,由题意得
(x﹣20)[25﹣(x﹣25)]=200,
化简得:x2﹣70x+1200=0,
解得:x1=30,x2=40,
∵销量尽可能大,
∴=30.
答:每盆花卉售价是30元;
(2)设该花卉一天的利润是w元,每盆售价是x元,由题意得
w=(x﹣20)[25﹣(x﹣25)]
=﹣x2+70x﹣1000
=﹣(x﹣35)2+225.
∵每盆花卉涨价不超过6元,
25≤a≤31.
∵a≤35时,w随x的增大而增大,
∴当a=31时,w有最大值为209.
答:该花卉一天最大的销售利润是209元.
12.某水果店销售一种新鲜水果,平均每天可售出120箱,每箱盈利60元,为了扩大销售减少库存,水果店决定采取适当的降价措施,经调查发现,每箱水果每降价5元,水果店平均每天可多售出20箱.设每箱水果降价x元.
(1)当x=10时,每箱利润 50 元,平均每天可售出 160 箱水果;
(2)设每天销售该水果的总利润为w元.
①求w与x之间的函数解析式;
②试判断w能否达到8200元,如果能达到,求出此时x的值;如果不能达到,求出w的最大值.
解:(1)根据题意,可知:当每箱水果降价10元时,每箱利润为60﹣10=50(元),平均每天可售出120+20×=160(箱).
故答案为:50;160;
(2)①由题意得w与x之间的函数解析式为w=(60﹣x)(120+×20)=﹣4x2+120x+7200;
②w不能达到8200元.
w=﹣4x2+120x+7200=﹣4(x﹣15)2+8100.
∵﹣4<0,
∴当x=15时,w取到最大值,
∵w最大值=8100<8200,
∴w不能达到8200元,
w的最大值是8100元.
13.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
解:(1)根据题意,得y=200﹣0.5×4(x﹣48)
=﹣2x+296,
∴y与x之间的函数关系式:y=﹣2x+296;
(2)根据题意,得W=(x﹣34)(﹣2x+296)
=﹣2(x﹣91)2+6498,
∵a=﹣2<0,
∴抛物线开口向下,W有最大值,
当x=91时,W最大值=6498,
答:每套售价定为:91元时,每天销售套件所获利润最大,最大利润是6498元.
14.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图7所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3m,运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
解:(1)∵抛物线的顶点坐标为(0,3.5),
∴设抛物线的解析式为y=ax2+3.5.
由题意可知,抛物线上的点B的坐标为(1.5,3.05).
∴2.25a+3.5=3.05,
解得a=﹣0.2,
∴抛物线的解析式为y=﹣0.2x2+3.5;
(2)设篮球出手时,运动员甲跳离地面的高度为h m.
4﹣1.5=2.5(m),0.25+1.8=2.05(m).
由题意可得点A的坐标为(﹣2.5,2.05+h),
∴2.05+h=﹣0.2×(﹣2.5)2+3.5,
∴h=0.2(m).
∴篮球出手时,运动员跳离地面的高度是0.2m;
(3)由题意可得出:y=3.3,
则3.3=﹣0.2x2+3.5
解得:x1=1,x2=﹣1,
∴2.5﹣1=1.5(m),1.5﹣1=0.5(m)
∴乙在距离甲1.5米以内或离篮板0.5米以内能在空中截住球.
15.某商品的进价为每件40元,售价为每件50元.每个月可卖出420件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为W元.求每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
解:∵每件售价不能高于65元,
∴x≤65﹣50,即x≤15,
根据题意得:W=(50+x﹣40)(420﹣10x)=﹣10x2+320x+4200=﹣10(x﹣16)2+6760,
∵﹣10<0,抛物线对称轴为直线x=16,
∴x=15时,W取最大值,最小值为﹣10×(15﹣16)2+6760=6750(元),
此时售价为50+x=50+15=65,
答:每件商品的售价定为65元时,每个月可获得最大利润,最大的月利润是6750元.
16.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
产品 每件售价(万元) 每件成本(万元) 每年其他费用(万元) 每年最大产销量(件)
甲 12 a 40 150
乙 18 8 40+0.05x2 80
其中a为常数,且5≤a≤10.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
解:(1)y1=(12﹣a)x﹣40(0<x≤150),
y2=(18﹣8)x﹣(40+0.05x2)=﹣0.05x2+10x﹣40(0<x≤80);
(2)对于y1=(12﹣a)x﹣40,
∵5≤a≤10,
∴12﹣a>0,
∴y1随x的增大而增大,
∴x=150时,y1取最大值,最大值为(1760﹣150a)万元;
对于y2=﹣0.05x2+10x﹣40=﹣0.05(x﹣100)2+460,
∵80<100,﹣0.05<0,
∴y2随x的增大而增大,
∴x=80时,y2取最大值,最大值是﹣0.05×(80﹣100)2+460=440(万元);
(3)①1760﹣150a=440,解得a=8.8,
②1760﹣150a>440,解得a<8.8,
③1760﹣150a<440,解得a>8.8,
∵5≤a≤10,
∴当a=8.8时,生产甲乙两种产品的利润相同,
当5≤a<8.8时,生产甲产品利润比较高,
当8.8<a≤10时,生产乙产品利润比较高.
17.某商品的成本w(单位:百元)由包装费和生产费两部分组成.其中当原料数量x(单位:千克)低于4千克时,包装费y1(单位:百元)与原料数量x之间的关系式为y1=1.2﹣0.3x;当原料数量不低于4千克时,包装费全免.生产费2(单位:百元)与原料数量x之间的关系式为:y2=ax2+0.1x(a>0).
(1)当原料数量x=3时,该商品的成本为: (9a+0.6) (百元);当原料数量x=5时,该商品的成本为: (25a+0.5) (百元);(直接用含a的式子表示)
(2)若a=0.1,求原料数量x为多少千克时,该商品的成本最少?最少是多少百元?
(3)若当原料数量低于4千克时,有且仅有唯一正整数x使得该商品的成本w不高于2百元,直接写出a的取值范围.
解:(1)由题意知w=y1+y2,y2=ax2+0.1x,
∴当x=3时,y1=1.2﹣0.3x,该商品成本为:1.2﹣0.3×3+a×32+0.1×3=9a+0.6;
当x=5时,y1=0,该商品的成本为:ax2+0.1x=a×52+0.1×5=25a+0.5;
故答案为:(9a+0.6);(25a+0.5);
(2)当a=0.1时,y2=0.1x2+0.1x,
当0<x<4时,成本w=1.2﹣0.3x+0.1x2+0.1x=0.1x2﹣0.2x+1.2=0.1(x﹣1)2+1.1,
∵0.1>0,
∴当x=1时,w有最小值为1.1百元;
当x≥4时,成本w=0.1x2+0.1x=0.1(x+0.5)2﹣0.025,
∵0.1>0,
∴当x=4时,w有最小值为2;
∵1.1<2,
∴原料数量为1千克时,该商品的成本最少,最少是1.1百元,;
(3)当0<x<4时,成本w=1.2﹣0.3x+ax2+0.1x=ax2﹣0.2x+1.2,
∵w≤2,
∴ax2﹣0.2x+1.2≤2,
整理得:ax2﹣0.2x﹣0.8≤0,
∵有唯一正整数x成立,
∴,
解得0.3<a≤1.
18.月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句小饼如嚼月,中有和饴赞美月饼.为满足市场需求,某蛋糕店在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是60元,蛋糕店规定每盒售价不得少于70元,根据以往销售经验发现:当售价定为每盒70元时,每天可卖出500盒,每盒售价每提高1元时,每天要少卖出20盒,请解答下列问题:
(1)若每盒月饼售价提高20元,则每天可卖出 100 盒,销售利润为 3000 元;
(2)设每天的销售利润为y元,每盒售价提高x元(x为整数),请求出γ与x之间的函数解析式,并直接写出当每盒售价定为多少元时,每天销售的总利润最大?最大利润是多少?
(3)为稳定物价,有关管理部]限定:这种月饼的每盒售价不得高出78元,如果蛋糕店想要每天获得6000元的利润,那么蛋糕店每天销售月饼 400 盒.
解:(1)根据题意得:若每盒月饼售价提高20元,则每天可卖出500﹣20×20=100(盒),销售利润为100×(70+20﹣60)=3000(元),
故答案为:100,3000;
(2)根据题意得:y=(70+x﹣60)(500﹣20x)=﹣20x2+300x+5000=﹣20(x﹣)2+6125,
∵﹣20<0,x为整数,
∴x=7或x=8时,y取最大值,最大值为﹣20×+6125=6120(元),
此时70+x=70+7=77或70+x=70+8=78,
答:y与x之间的函数解析式为y=﹣20x2+300x+5000,当每盒售价定为77元或78元时,每天销售的总利润最大,最大利润是6120元;
(3)在y=﹣20x2+300x+5000中,令y=6000得;
﹣20x2+300x+5000=6000,
解得x=5或x=10,
当x=5时,售价为70+x=70+5=75<78,此时蛋糕店每天销售月饼500﹣20x=500﹣20×5=400(盒),
当x=10时,售价70+x=70+10=80>78,
∴x=10不符合题意,
答:蛋糕店每天销售月饼400盒,
故答案为:400.
19.一名男生推铅球,其铅球运行的路线如图,是抛物线的一部分.当水平距离x为3米时,铅球的行进高度y达到最高2米.已知推出铅球的初始高度是米.
(1)求铅球运行路线的解析式;
(2)求铅球推出的水平距离OA.
解:(1)设二次函数的解析式为y=a(x﹣3)2+2,
把(0,)代入上式得=a(0﹣3)2+2,
解得a=﹣,
则二次函数的解析式为:y=﹣(x﹣3)2+2;
(2)由题意可得:﹣(x﹣3)2+2=0,
解得x1=﹣3(舍去),x2=9,
∴OA=9m,
则铅球推出的距离为9m.
20.某公司的商品进价每件60元,售价每件130元,为了支持“抗新冠肺炎”,每销售一件捐款4元.且未来30天,该商品将开展每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,市场调查发现,设第x天(1≤x≤30且x为整数)的销量为y件,y与x满足一次函数关系,其对应数据如表:
x(天) … 1 3 5 7 …
y(件) … 35 45 55 65 …
(1)直接写出y与x的函数关系式;
(2)设第x天去掉捐款后的利润为W元,试求出W与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
解:(1)设y与x满足的一次函数数关系式为y=kx+b(k≠0),
将(1.35),(3,45)分别代入得,
解得,
∴y与x的函数关系式为y=5x+30;
(2)由题意得W=(130﹣x﹣60﹣4)(5x+30)
=﹣5x2+300x+1980
=﹣5(x﹣30)2+6480,
∵a=﹣5<0,
∴当x=30时,W有最大值,最大值为6480元.
∴W与x之间的函数关系式是W=﹣5(x﹣30)2+6480,第30天的利润最大,最大利润是6480元.
21.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元(x≥100).
(1)每天有游客居住的房间数为 ﹣x+30 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
解:(1)根据题意知,每间房间定价x元时,每天有游客居住的房间数为20﹣=﹣x+30;
故答案为:﹣x+30;
(2))∵该天利润为1870元,
∴(﹣x+30)(x﹣20)=1870,
解得x=130或x=190,
答:这天每间房的定价是130元或190元;
(3)根据题意得:w=(﹣x+30)(x﹣20)=﹣x2+32x﹣600=﹣(x﹣160)2+1960,
∵﹣<0,
∴当x=160时,w取最大值,最大值为1960元;
答:当每间房价定为160元,宾馆的利润w最大为1960元.
22.2022年体育中考,增设了考生进入考点需进行体温检测的要求,防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数y(人)与时间x(分钟)的变化情况,数据如表:
时间x(分钟) 0 1 2 3 4 5 6 7 8 9 9≤x
人数y(人) 0 170 320 450 560 650 720 770 800 810 810
(1)分析前9分钟内考生进入考点的累计人数与时间的变化规律,发现它符合二次函数的模型,你能求出这段时间内y与x之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
解:(1)由表格中数据的变化趋势可知,
①当0≤x≤9时,y是x的二次函数,
∵当x=0时,y=0,
∴二次函数的关系式可设为:y=ax2+bx,
由题意可得:,
解得:,
∴二次函数关系式为:y=﹣10x2+180x,
②当x>9时,y=810,
∴y与x之间的函数关系式为:y=;
(2)设第x分钟时的排队人数为w人,
由题意可得:w=y﹣2×20x=,
①当0≤x≤9时,w=﹣10x2+140x=﹣10(x﹣7)2+490,
∴当x=7时,w的最大值为490,
②当x>9时,w=810﹣40x,w随x的增大而减小,
∴w<450,
∴排队人数最多时是490人,
要全部考生都完成体温检测,根据题意得:810﹣40x=0,
解得:x=20.25,
答:排队人数最多时有490人,全部考生都完成体温检测需要20.25分钟.
23.如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣12)2+h,小明罚任意球时防守队员站在小明正前方9m处组成人墙,防守队员的身高为2.1m,对手球门与小明的水平距离为18m,已知足球球门高为2.43m.假定小明罚出的任意球恰好射正对手球门.
(1)当h=3时,求y与x的关系式;
(2)当h=3时,足球能否越过人墙?足球会不会踢飞?请说明理由;
(3)若小明罚出的任意球一定能直接射进对手球门得分,求h的取值范围.
解:(1)当h=3时,y=a(x﹣12)2+3,
∵抛物线y=a(x﹣12)2+3经过点(0,0),
∴0=a(0﹣12)2+3,
解得:a=﹣,
∴y与x的关系式y=﹣(x﹣12)2+3(0≤x≤24);
(2)当h=3时,足球能越过人墙,足球不会踢飞,理由如下:
当h=3时,由(1)得y=﹣(x﹣12)2+3,
当x=9时,y=﹣(9﹣12)2+3≈2.81>2.1,
∴足球能过人墙,
当x=18时,y=﹣(18﹣12)2+3=2.25<2.43,
∴足球能直接射进球门;
(3)由题设知y=a(x﹣12)2+h,函数图象过点(0,0),
得0=a(0﹣12)2+h,即144a+h=0①,
由足球能越过人墙,得9a+h>2.1②,
由足球能直接射进球门,得0<36a+h<2.43③,
由①得a=﹣④,
把④代入②得9×(﹣)+h>2.1,
解得h>2.24,
把④代入③得0<36×(﹣)+h<2.43,
解得0<h<3.24,
∴h的取值范围是2.24<h<3.24.
24.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为x米,与湖面的垂直高度为y米.下面的表中记录了x与y的五组数据:
x(米) 0 1 2 3 4
y(米) 0.5 1.25 1.5 1.25 0.5
(1)在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示y与x函数关系的图象;
(2)求y与x函数表达式;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).
解:(1)以喷泉与湖面的交点为原点,喷泉所在的直线为纵轴建立平面直角坐标系,如图1所示:
(2)根据图象可设二次函数的解析式为:y=a(x﹣2)2+1.5,
将(0,0.5)代入y=a(x﹣2)2+1.5,
解得a=﹣,
∴抛物线的解析式为:y=﹣x2+x+0.5;
(3)设调节后的水管喷出的抛物线的解析式为:y=﹣x2+x+0.5+n,
由题意可知,当横坐标为2+=时,纵坐标的值不小于2+0.5=2.5,
∴﹣×()2++0.5+n≥2.5,
解得n≥,
∴水管高度至少向上调节米,
∴0.5+≈2.1(米),
∴公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到约2.1米才能符合要求.
25.某公司生产的某种时令商品每件成本为20元,经过市场调研发现:
①这种商品在未来40天内的日销售量m(件)与时间t(天)的关系为:m=﹣2t+96.
②未来40天内,该商品每天的单价y(元/件)与时间t(天)(t为整数)之间关系的函数图象如图所示.
请结合上述信息解决下列问题:
(1)经计算得,当0<t≤20时,y关于t的函数关系式为 y=t+25 ;则当20<t≤40时,y关于t的函数关系式为 y=﹣t+40 .
(2)请预测未来40天中哪一天的单价是27元?
(3)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
解:(1)当0<t≤20时,y关于t的函数关系式为y=mt+n,
则,
解得,
∴y关于t的函数关系式为:y=t+25;
当20<t≤40时,y关于t的函数关系式为y=at+b,
则,
解得,
∴y关于t的函数关系式为:y=﹣t+40;
故答案为:y=t+25;y=﹣t+40;
(2)①当0<t≤20时,
令t+25=27,
解得t=8,
②当20<t≤40时,
令﹣t+40=27,
解得:t=26,
∴未来40天中第8天和第26天的单价是27元;
(3)前20天的销售利润为P1元,后20天的销售利润为P2元,
则P1=(﹣2t+96)(t+25﹣20)
=﹣(t﹣14)2+578,
∵﹣<0,
∴当t=14时,P1有最大值,为578元;
P2=(﹣2t+96)(﹣t+40﹣20)
=t2﹣88t+1920
=(t﹣44)2﹣16,
∵1>0,
∴当21≤t≤40时,P2随t的增大而减小,
∴当t=21时,P2最大,为513元,
∴第14天利润最大,最大利润为578元.
二次函数的应用解答题专项练习
1.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.
2.第二十届省运会于2022年在泰州举行,运动会纪念微章在某网店上进行销售.当每枚售价20元时,平均每天可售出100枚为了扩大销售,现采取了降价措施,在每枚售价不少于15元的前提下,销售一段时间后,发现销售单价每降低I元,平均每天可多售出10枚.若每枚微章降价a(a为正数)元.
(1)降价后平均每天销售数量为 枚(用含a的代数式表示),a的取值范围是 ;
(2)当该网店每天销售额为2210元时,求a的值.
3.如图,二小球从斜坡A点处抛出,正好穿过B点的篮筐,落在斜坡底部的O点,以O为坐标原点建立直角坐标系,B的坐标为(,),斜坡的坡比为1:2,A点距地面的高度为1.5米,球的抛出路线可以用二次函数刻画.
(1)求二次函数的表达式;
(2)求小球到达的最高点的坐标.
4.水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的变化规律符合一次函数关系,部分数据如表:
销售时间t(1≤t≤15,t为整数)(天) 1 4 5 8 12
销售单价p(元/千克) 20.25 21 21.25 22 23
(1)试求p关于t的函数解析式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=﹣2t+120(1≤t≤15,t为整数).求销售过程中最大日销售利润为多少?
5.如图1,是某种音乐喷泉,其形状如抛物线,图2是它的示意图,喷头A到地面BC的距离AO为5m,抛物线AEB与AFC关于AO对称,点D在抛物线AFC的最高处,离地面BC的距离为6m.到AO的距离为1m,已知喷泉的落地点中,B,C间距离最远.
(1)请建立恰当的平面直角坐标系,求抛物线AEB的解析式;
(2)要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须满足什么条件?
6.双手头上前掷实心球是锻炼青少年上肢力量和全身协调性的一个项目,实心球出手后飞行的路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,某校一名学生在投掷实心球时,从出手到落地的过程中,实心球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣x2+x+2.
(1)求该同学投掷实心球时,实心球在空中飞行时竖直高度的最大值;
(2)判断并说明,该同学此次投掷实心球的水平距离能否超过10米.
7.某大桥上正在行驶的甲车,发现正前方27m处沿同一方向行驶的乙车(此时v甲>v乙)后,开始减速,减速后甲车行驶的路程s(单位:m)与速度v(单位:m/s)之间的关系式为s=﹣v2+128(0≤v≤16);甲车行驶的速度v(单位:m/s)与时间t(单位:s)的关系可以用一次函数表示(如图).
(1)当甲车减速4s时,它行驶的路程是多少?
(2)若乙车以一定的速度一直匀速行驶,经过多长时间两车之间的最近距离是2.5m?(提示:甲车减速后,当甲、乙两车速度相同时,车距最小)
8.某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值.
9.温州某百货商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元(x≥7).
(1)该商品每天的销售量: (用含x的代数式表示);
(2)若该商场当天销售这种商品所获得的利润为480元,求x的值.
(3)当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?此时最大利润为多少?
10.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元
(1)如果销售单价定为25元,那么健身球每天的销售量是 个;
(2)求w与x之间的函数关系式;
(3)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
11.“十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.
(1)若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?
(2)为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?
12.某水果店销售一种新鲜水果,平均每天可售出120箱,每箱盈利60元,为了扩大销售减少库存,水果店决定采取适当的降价措施,经调查发现,每箱水果每降价5元,水果店平均每天可多售出20箱.设每箱水果降价x元.
(1)当x=10时,每箱利润 元,平均每天可售出 箱水果;
(2)设每天销售该水果的总利润为w元.
①求w与x之间的函数解析式;
②试判断w能否达到8200元,如果能达到,求出此时x的值;如果不能达到,求出w的最大值.
13.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
14.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图7所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3m,运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
15.某商品的进价为每件40元,售价为每件50元.每个月可卖出420件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为W元.求每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
16.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
产品 每件售价(万元) 每件成本(万元) 每年其他费用(万元) 每年最大产销量(件)
甲 12 a 40 150
乙 18 8 40+0.05x2 80
其中a为常数,且5≤a≤10.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
17.某商品的成本w(单位:百元)由包装费和生产费两部分组成.其中当原料数量x(单位:千克)低于4千克时,包装费y1(单位:百元)与原料数量x之间的关系式为y1=1.2﹣0.3x;当原料数量不低于4千克时,包装费全免.生产费2(单位:百元)与原料数量x之间的关系式为:y2=ax2+0.1x(a>0).
(1)当原料数量x=3时,该商品的成本为: (百元);当原料数量x=5时,该商品的成本为: (百元);(直接用含a的式子表示)
(2)若a=0.1,求原料数量x为多少千克时,该商品的成本最少?最少是多少百元?
(3)若当原料数量低于4千克时,有且仅有唯一正整数x使得该商品的成本w不高于2百元,直接写出a的取值范围.
18.月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句小饼如嚼月,中有和饴赞美月饼.为满足市场需求,某蛋糕店在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是60元,蛋糕店规定每盒售价不得少于70元,根据以往销售经验发现:当售价定为每盒70元时,每天可卖出500盒,每盒售价每提高1元时,每天要少卖出20盒,请解答下列问题:
(1)若每盒月饼售价提高20元,则每天可卖出 盒,销售利润为 元;
(2)设每天的销售利润为y元,每盒售价提高x元(x为整数),请求出γ与x之间的函数解析式,并直接写出当每盒售价定为多少元时,每天销售的总利润最大?最大利润是多少?
(3)为稳定物价,有关管理部]限定:这种月饼的每盒售价不得高出78元,如果蛋糕店想要每天获得6000元的利润,那么蛋糕店每天销售月饼 盒.
19.一名男生推铅球,其铅球运行的路线如图,是抛物线的一部分.当水平距离x为3米时,铅球的行进高度y达到最高2米.已知推出铅球的初始高度是米.
(1)求铅球运行路线的解析式;
(2)求铅球推出的水平距离OA.
20.某公司的商品进价每件60元,售价每件130元,为了支持“抗新冠肺炎”,每销售一件捐款4元.且未来30天,该商品将开展每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,市场调查发现,设第x天(1≤x≤30且x为整数)的销量为y件,y与x满足一次函数关系,其对应数据如表:
x(天) … 1 3 5 7 …
y(件) … 35 45 55 65 …
(1)直接写出y与x的函数关系式;
(2)设第x天去掉捐款后的利润为W元,试求出W与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
21.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元(x≥100).
(1)每天有游客居住的房间数为 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
22.2022年体育中考,增设了考生进入考点需进行体温检测的要求,防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数y(人)与时间x(分钟)的变化情况,数据如表:
时间x(分钟) 0 1 2 3 4 5 6 7 8 9 9≤x
人数y(人) 0 170 320 450 560 650 720 770 800 810 810
(1)分析前9分钟内考生进入考点的累计人数与时间的变化规律,发现它符合二次函数的模型,你能求出这段时间内y与x之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
23.如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣12)2+h,小明罚任意球时防守队员站在小明正前方9m处组成人墙,防守队员的身高为2.1m,对手球门与小明的水平距离为18m,已知足球球门高为2.43m.假定小明罚出的任意球恰好射正对手球门.
(1)当h=3时,求y与x的关系式;
(2)当h=3时,足球能否越过人墙?足球会不会踢飞?请说明理由;
(3)若小明罚出的任意球一定能直接射进对手球门得分,求h的取值范围.
24.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为x米,与湖面的垂直高度为y米.下面的表中记录了x与y的五组数据:
x(米) 0 1 2 3 4
y(米) 0.5 1.25 1.5 1.25 0.5
(1)在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示y与x函数关系的图象;
(2)求y与x函数表达式;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).
25.某公司生产的某种时令商品每件成本为20元,经过市场调研发现:
①这种商品在未来40天内的日销售量m(件)与时间t(天)的关系为:m=﹣2t+96.
②未来40天内,该商品每天的单价y(元/件)与时间t(天)(t为整数)之间关系的函数图象如图所示.
请结合上述信息解决下列问题:
(1)经计算得,当0<t≤20时,y关于t的函数关系式为 ;则当20<t≤40时,y关于t的函数关系式为 .
(2)请预测未来40天中哪一天的单价是27元?
(3)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
参考答案
1.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.
解:∵h=﹣5t2+20t=﹣5(t﹣2)2+20,
且﹣5<0,
∴当t=2时,h取最大值20,
答:小球飞行高度达到最高时的飞行时间为2s.
2.第二十届省运会于2022年在泰州举行,运动会纪念微章在某网店上进行销售.当每枚售价20元时,平均每天可售出100枚为了扩大销售,现采取了降价措施,在每枚售价不少于15元的前提下,销售一段时间后,发现销售单价每降低I元,平均每天可多售出10枚.若每枚微章降价a(a为正数)元.
(1)降价后平均每天销售数量为 (100+10a) 枚(用含a的代数式表示),a的取值范围是 0<a≤5 ;
(2)当该网店每天销售额为2210元时,求a的值.
解:(1)∵销售单价每降低1元,平均每天可多售出10枚,
∴每枚商品降价a元,平均每天多售出10a枚,
∵降价前平均每天可售出100枚,
∴降价后平均每天可售出(100+10a)枚,
∵每枚售价不少于15元,降价后售价为(20﹣a)元,
∴20﹣a≥15,
解得:0<a≤5,
故答案为:(100+10a),0<a≤5;
(2)由(1)知:(20﹣a)(100+10a)=2210,
整理得:a2﹣10a+21=0,
解得:a1=3,a2=7,
∵a≤5,
∴a=3.
3.如图,二小球从斜坡A点处抛出,正好穿过B点的篮筐,落在斜坡底部的O点,以O为坐标原点建立直角坐标系,B的坐标为(,),斜坡的坡比为1:2,A点距地面的高度为1.5米,球的抛出路线可以用二次函数刻画.
(1)求二次函数的表达式;
(2)求小球到达的最高点的坐标.
解:(1)过A作AD⊥x轴,垂足为D,如图:
∵斜坡的坡比为1:2,
∴AD:OD=1:2,
∵AD=1.5,
∴OD=3,
∴A(3,1.5),
设二次函数的表达式为y=ax2+bx,
将A(3,1.5)、B(,)两点坐标代入得:
,
解得,
∴二次函数的表达式为y=﹣x2+2x;
(2)∵y=﹣x2+2x=﹣(x﹣2)2+2,
且﹣<0,
∴当x=2时,y取最大值2,
∴小球到达的最高点的坐标为(2,2).
4.水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的变化规律符合一次函数关系,部分数据如表:
销售时间t(1≤t≤15,t为整数)(天) 1 4 5 8 12
销售单价p(元/千克) 20.25 21 21.25 22 23
(1)试求p关于t的函数解析式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=﹣2t+120(1≤t≤15,t为整数).求销售过程中最大日销售利润为多少?
解:(1)设p与t之间的变化的一次函数关系为:p=kt+b,
将点(4,21)、(8,22)代入上式得:,
解得:,
故p关于t的函数表达式为:p=t+20(1≤t≤15,t为整数);
(2)设日销售利润为w,
由题意得:w=y(p﹣10)=(﹣2t+120)(t+20﹣10)=﹣(t﹣10)2+1250(1≤t≤15,t为整数),
∵﹣<0,
∴当t=10时,w有最大值,最大值为1250;
答:销售过程中最大日销售利润为1250元.
5.如图1,是某种音乐喷泉,其形状如抛物线,图2是它的示意图,喷头A到地面BC的距离AO为5m,抛物线AEB与AFC关于AO对称,点D在抛物线AFC的最高处,离地面BC的距离为6m.到AO的距离为1m,已知喷泉的落地点中,B,C间距离最远.
(1)请建立恰当的平面直角坐标系,求抛物线AEB的解析式;
(2)要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须满足什么条件?
解:(1)以O为原点,以BC所在直线为x轴,以AO所在直线为y轴建立平面直角坐标系,如图所示:
由题意知,A(0,5),D(1,6),
∵抛物线AEB与AFC关于AO对称,
∴抛物线AEB的顶点坐标为(﹣1,6),
设抛物线AEB的解析式为y=a(x+1)2+6,
把A(0,5)代入解析式得:5=a(0+1)2+6,
解得a=﹣1,
∴抛物线AEB的解析式为y=﹣(x+1)2+6;
(2)令y=0,则﹣(x+1)2+6=0,
解得x1=﹣1+,x2=﹣1﹣(舍去),
∴BC=2OB=﹣2+2.
答:要使喷出的水落到圆形水池内,建造水池时,水池的直径d必须大于﹣2+2.
6.双手头上前掷实心球是锻炼青少年上肢力量和全身协调性的一个项目,实心球出手后飞行的路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,某校一名学生在投掷实心球时,从出手到落地的过程中,实心球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣x2+x+2.
(1)求该同学投掷实心球时,实心球在空中飞行时竖直高度的最大值;
(2)判断并说明,该同学此次投掷实心球的水平距离能否超过10米.
解:(1)y=﹣x2+x+2=﹣(x2﹣6x)+2=﹣(x﹣3)2+,
∵﹣<0,
∴当x=3时,y有最大值,最大值为,
答:实心球在空中飞行时竖直高度的最大值为;
(2)令y=0,则=﹣x2+x+2=0,
解得x1=﹣2,x2=8,
∵8<10,
∴该同学此次投掷实心球的水平距离不能超过10米.
7.某大桥上正在行驶的甲车,发现正前方27m处沿同一方向行驶的乙车(此时v甲>v乙)后,开始减速,减速后甲车行驶的路程s(单位:m)与速度v(单位:m/s)之间的关系式为s=﹣v2+128(0≤v≤16);甲车行驶的速度v(单位:m/s)与时间t(单位:s)的关系可以用一次函数表示(如图).
(1)当甲车减速4s时,它行驶的路程是多少?
(2)若乙车以一定的速度一直匀速行驶,经过多长时间两车之间的最近距离是2.5m?(提示:甲车减速后,当甲、乙两车速度相同时,车距最小)
解:(1)设一次函数表达式为v=kt+b,
∵一次函数经过(3,13),(6,10),
则,
解得,
∴一次函数表达式为v=﹣t+16,
∴当t=4时,速度为12m/s,
∴当v=12时,s=﹣v2+128=﹣m,
∴当甲车减速4s时,它行驶的路程是56m;
(2)当v甲>v乙时,两车之间的距离逐渐变小,当v甲<v乙时,两车之间的距离逐渐变大,
∴当两车速度相等时,两车之间距离最小.
根据题意,得:S甲+2.5=27+S乙,
∴﹣(t﹣16)2+128+2.5=27+(t﹣16)t,
化简,得:t2=49.
∴t1=7,t2=﹣7(舍).
答:经过7s两车相距的最近距离是2.5m.
8.某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值.
解:(1)根据题意得:S=(250﹣200) 10y﹣x=500(﹣0.001x2+0.06x+1)﹣x=﹣x2+29x+500,
∴年利润S(万元)与广告费用x(万元)的函数关系式为S=﹣x2+29x+500;
(2)∵S=﹣(x﹣29)2+920.5(10≤x≤50),
∴当10≤x<29时,S随着x的增大而增大;
当29<x≤50时,S随着x的增大而减小;
当x=29时,S有最大值920.5.
故年利润S的最大值为920.5万元.
9.温州某百货商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元(x≥7).
(1)该商品每天的销售量: (﹣20x+300)元 (用含x的代数式表示);
(2)若该商场当天销售这种商品所获得的利润为480元,求x的值.
(3)当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?此时最大利润为多少?
解:(1)根据题意得,160﹣20(x﹣7)=﹣20x+300,
故答案为:(﹣20x+300)元;
(2)根据题意得,(x﹣5)(﹣20x+300)=480,
解得x=9或11;
(3)设销售的总利润为y元,根据题意得,
y=(x﹣5)(﹣20x+300)=﹣20x2+400x﹣1500=﹣20(x﹣10)2+500,
∴当x=10时,y有最大值为500,
答:当商品的销售单价定为10元时,该商店销售这种商品获得的利润最大,此时最大利润为500元.
10.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元
(1)如果销售单价定为25元,那么健身球每天的销售量是 30 个;
(2)求w与x之间的函数关系式;
(3)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
解:(1)在y=﹣2x+80中,令x=25得:
y=﹣2×25+80=30,
故答案为:30;
(2)根据题意得:w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600,
∴w与x之间的函数关系式为w=﹣2x2+120x﹣1600;
(3)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w取最大值,最大值为200,
答:该种健身球销售单价定为30元时,每天的销售利润最大,最大利润是200元.
11.“十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.
(1)若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?
(2)为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?
解:(1)设该花卉每盆售价是x元,由题意得
(x﹣20)[25﹣(x﹣25)]=200,
化简得:x2﹣70x+1200=0,
解得:x1=30,x2=40,
∵销量尽可能大,
∴=30.
答:每盆花卉售价是30元;
(2)设该花卉一天的利润是w元,每盆售价是x元,由题意得
w=(x﹣20)[25﹣(x﹣25)]
=﹣x2+70x﹣1000
=﹣(x﹣35)2+225.
∵每盆花卉涨价不超过6元,
25≤a≤31.
∵a≤35时,w随x的增大而增大,
∴当a=31时,w有最大值为209.
答:该花卉一天最大的销售利润是209元.
12.某水果店销售一种新鲜水果,平均每天可售出120箱,每箱盈利60元,为了扩大销售减少库存,水果店决定采取适当的降价措施,经调查发现,每箱水果每降价5元,水果店平均每天可多售出20箱.设每箱水果降价x元.
(1)当x=10时,每箱利润 50 元,平均每天可售出 160 箱水果;
(2)设每天销售该水果的总利润为w元.
①求w与x之间的函数解析式;
②试判断w能否达到8200元,如果能达到,求出此时x的值;如果不能达到,求出w的最大值.
解:(1)根据题意,可知:当每箱水果降价10元时,每箱利润为60﹣10=50(元),平均每天可售出120+20×=160(箱).
故答案为:50;160;
(2)①由题意得w与x之间的函数解析式为w=(60﹣x)(120+×20)=﹣4x2+120x+7200;
②w不能达到8200元.
w=﹣4x2+120x+7200=﹣4(x﹣15)2+8100.
∵﹣4<0,
∴当x=15时,w取到最大值,
∵w最大值=8100<8200,
∴w不能达到8200元,
w的最大值是8100元.
13.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
解:(1)根据题意,得y=200﹣0.5×4(x﹣48)
=﹣2x+296,
∴y与x之间的函数关系式:y=﹣2x+296;
(2)根据题意,得W=(x﹣34)(﹣2x+296)
=﹣2(x﹣91)2+6498,
∵a=﹣2<0,
∴抛物线开口向下,W有最大值,
当x=91时,W最大值=6498,
答:每套售价定为:91元时,每天销售套件所获利润最大,最大利润是6498元.
14.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图7所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3m,运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
解:(1)∵抛物线的顶点坐标为(0,3.5),
∴设抛物线的解析式为y=ax2+3.5.
由题意可知,抛物线上的点B的坐标为(1.5,3.05).
∴2.25a+3.5=3.05,
解得a=﹣0.2,
∴抛物线的解析式为y=﹣0.2x2+3.5;
(2)设篮球出手时,运动员甲跳离地面的高度为h m.
4﹣1.5=2.5(m),0.25+1.8=2.05(m).
由题意可得点A的坐标为(﹣2.5,2.05+h),
∴2.05+h=﹣0.2×(﹣2.5)2+3.5,
∴h=0.2(m).
∴篮球出手时,运动员跳离地面的高度是0.2m;
(3)由题意可得出:y=3.3,
则3.3=﹣0.2x2+3.5
解得:x1=1,x2=﹣1,
∴2.5﹣1=1.5(m),1.5﹣1=0.5(m)
∴乙在距离甲1.5米以内或离篮板0.5米以内能在空中截住球.
15.某商品的进价为每件40元,售价为每件50元.每个月可卖出420件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为W元.求每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
解:∵每件售价不能高于65元,
∴x≤65﹣50,即x≤15,
根据题意得:W=(50+x﹣40)(420﹣10x)=﹣10x2+320x+4200=﹣10(x﹣16)2+6760,
∵﹣10<0,抛物线对称轴为直线x=16,
∴x=15时,W取最大值,最小值为﹣10×(15﹣16)2+6760=6750(元),
此时售价为50+x=50+15=65,
答:每件商品的售价定为65元时,每个月可获得最大利润,最大的月利润是6750元.
16.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
产品 每件售价(万元) 每件成本(万元) 每年其他费用(万元) 每年最大产销量(件)
甲 12 a 40 150
乙 18 8 40+0.05x2 80
其中a为常数,且5≤a≤10.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
解:(1)y1=(12﹣a)x﹣40(0<x≤150),
y2=(18﹣8)x﹣(40+0.05x2)=﹣0.05x2+10x﹣40(0<x≤80);
(2)对于y1=(12﹣a)x﹣40,
∵5≤a≤10,
∴12﹣a>0,
∴y1随x的增大而增大,
∴x=150时,y1取最大值,最大值为(1760﹣150a)万元;
对于y2=﹣0.05x2+10x﹣40=﹣0.05(x﹣100)2+460,
∵80<100,﹣0.05<0,
∴y2随x的增大而增大,
∴x=80时,y2取最大值,最大值是﹣0.05×(80﹣100)2+460=440(万元);
(3)①1760﹣150a=440,解得a=8.8,
②1760﹣150a>440,解得a<8.8,
③1760﹣150a<440,解得a>8.8,
∵5≤a≤10,
∴当a=8.8时,生产甲乙两种产品的利润相同,
当5≤a<8.8时,生产甲产品利润比较高,
当8.8<a≤10时,生产乙产品利润比较高.
17.某商品的成本w(单位:百元)由包装费和生产费两部分组成.其中当原料数量x(单位:千克)低于4千克时,包装费y1(单位:百元)与原料数量x之间的关系式为y1=1.2﹣0.3x;当原料数量不低于4千克时,包装费全免.生产费2(单位:百元)与原料数量x之间的关系式为:y2=ax2+0.1x(a>0).
(1)当原料数量x=3时,该商品的成本为: (9a+0.6) (百元);当原料数量x=5时,该商品的成本为: (25a+0.5) (百元);(直接用含a的式子表示)
(2)若a=0.1,求原料数量x为多少千克时,该商品的成本最少?最少是多少百元?
(3)若当原料数量低于4千克时,有且仅有唯一正整数x使得该商品的成本w不高于2百元,直接写出a的取值范围.
解:(1)由题意知w=y1+y2,y2=ax2+0.1x,
∴当x=3时,y1=1.2﹣0.3x,该商品成本为:1.2﹣0.3×3+a×32+0.1×3=9a+0.6;
当x=5时,y1=0,该商品的成本为:ax2+0.1x=a×52+0.1×5=25a+0.5;
故答案为:(9a+0.6);(25a+0.5);
(2)当a=0.1时,y2=0.1x2+0.1x,
当0<x<4时,成本w=1.2﹣0.3x+0.1x2+0.1x=0.1x2﹣0.2x+1.2=0.1(x﹣1)2+1.1,
∵0.1>0,
∴当x=1时,w有最小值为1.1百元;
当x≥4时,成本w=0.1x2+0.1x=0.1(x+0.5)2﹣0.025,
∵0.1>0,
∴当x=4时,w有最小值为2;
∵1.1<2,
∴原料数量为1千克时,该商品的成本最少,最少是1.1百元,;
(3)当0<x<4时,成本w=1.2﹣0.3x+ax2+0.1x=ax2﹣0.2x+1.2,
∵w≤2,
∴ax2﹣0.2x+1.2≤2,
整理得:ax2﹣0.2x﹣0.8≤0,
∵有唯一正整数x成立,
∴,
解得0.3<a≤1.
18.月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句小饼如嚼月,中有和饴赞美月饼.为满足市场需求,某蛋糕店在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是60元,蛋糕店规定每盒售价不得少于70元,根据以往销售经验发现:当售价定为每盒70元时,每天可卖出500盒,每盒售价每提高1元时,每天要少卖出20盒,请解答下列问题:
(1)若每盒月饼售价提高20元,则每天可卖出 100 盒,销售利润为 3000 元;
(2)设每天的销售利润为y元,每盒售价提高x元(x为整数),请求出γ与x之间的函数解析式,并直接写出当每盒售价定为多少元时,每天销售的总利润最大?最大利润是多少?
(3)为稳定物价,有关管理部]限定:这种月饼的每盒售价不得高出78元,如果蛋糕店想要每天获得6000元的利润,那么蛋糕店每天销售月饼 400 盒.
解:(1)根据题意得:若每盒月饼售价提高20元,则每天可卖出500﹣20×20=100(盒),销售利润为100×(70+20﹣60)=3000(元),
故答案为:100,3000;
(2)根据题意得:y=(70+x﹣60)(500﹣20x)=﹣20x2+300x+5000=﹣20(x﹣)2+6125,
∵﹣20<0,x为整数,
∴x=7或x=8时,y取最大值,最大值为﹣20×+6125=6120(元),
此时70+x=70+7=77或70+x=70+8=78,
答:y与x之间的函数解析式为y=﹣20x2+300x+5000,当每盒售价定为77元或78元时,每天销售的总利润最大,最大利润是6120元;
(3)在y=﹣20x2+300x+5000中,令y=6000得;
﹣20x2+300x+5000=6000,
解得x=5或x=10,
当x=5时,售价为70+x=70+5=75<78,此时蛋糕店每天销售月饼500﹣20x=500﹣20×5=400(盒),
当x=10时,售价70+x=70+10=80>78,
∴x=10不符合题意,
答:蛋糕店每天销售月饼400盒,
故答案为:400.
19.一名男生推铅球,其铅球运行的路线如图,是抛物线的一部分.当水平距离x为3米时,铅球的行进高度y达到最高2米.已知推出铅球的初始高度是米.
(1)求铅球运行路线的解析式;
(2)求铅球推出的水平距离OA.
解:(1)设二次函数的解析式为y=a(x﹣3)2+2,
把(0,)代入上式得=a(0﹣3)2+2,
解得a=﹣,
则二次函数的解析式为:y=﹣(x﹣3)2+2;
(2)由题意可得:﹣(x﹣3)2+2=0,
解得x1=﹣3(舍去),x2=9,
∴OA=9m,
则铅球推出的距离为9m.
20.某公司的商品进价每件60元,售价每件130元,为了支持“抗新冠肺炎”,每销售一件捐款4元.且未来30天,该商品将开展每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,市场调查发现,设第x天(1≤x≤30且x为整数)的销量为y件,y与x满足一次函数关系,其对应数据如表:
x(天) … 1 3 5 7 …
y(件) … 35 45 55 65 …
(1)直接写出y与x的函数关系式;
(2)设第x天去掉捐款后的利润为W元,试求出W与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
解:(1)设y与x满足的一次函数数关系式为y=kx+b(k≠0),
将(1.35),(3,45)分别代入得,
解得,
∴y与x的函数关系式为y=5x+30;
(2)由题意得W=(130﹣x﹣60﹣4)(5x+30)
=﹣5x2+300x+1980
=﹣5(x﹣30)2+6480,
∵a=﹣5<0,
∴当x=30时,W有最大值,最大值为6480元.
∴W与x之间的函数关系式是W=﹣5(x﹣30)2+6480,第30天的利润最大,最大利润是6480元.
21.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元(x≥100).
(1)每天有游客居住的房间数为 ﹣x+30 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
解:(1)根据题意知,每间房间定价x元时,每天有游客居住的房间数为20﹣=﹣x+30;
故答案为:﹣x+30;
(2))∵该天利润为1870元,
∴(﹣x+30)(x﹣20)=1870,
解得x=130或x=190,
答:这天每间房的定价是130元或190元;
(3)根据题意得:w=(﹣x+30)(x﹣20)=﹣x2+32x﹣600=﹣(x﹣160)2+1960,
∵﹣<0,
∴当x=160时,w取最大值,最大值为1960元;
答:当每间房价定为160元,宾馆的利润w最大为1960元.
22.2022年体育中考,增设了考生进入考点需进行体温检测的要求,防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数y(人)与时间x(分钟)的变化情况,数据如表:
时间x(分钟) 0 1 2 3 4 5 6 7 8 9 9≤x
人数y(人) 0 170 320 450 560 650 720 770 800 810 810
(1)分析前9分钟内考生进入考点的累计人数与时间的变化规律,发现它符合二次函数的模型,你能求出这段时间内y与x之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
解:(1)由表格中数据的变化趋势可知,
①当0≤x≤9时,y是x的二次函数,
∵当x=0时,y=0,
∴二次函数的关系式可设为:y=ax2+bx,
由题意可得:,
解得:,
∴二次函数关系式为:y=﹣10x2+180x,
②当x>9时,y=810,
∴y与x之间的函数关系式为:y=;
(2)设第x分钟时的排队人数为w人,
由题意可得:w=y﹣2×20x=,
①当0≤x≤9时,w=﹣10x2+140x=﹣10(x﹣7)2+490,
∴当x=7时,w的最大值为490,
②当x>9时,w=810﹣40x,w随x的增大而减小,
∴w<450,
∴排队人数最多时是490人,
要全部考生都完成体温检测,根据题意得:810﹣40x=0,
解得:x=20.25,
答:排队人数最多时有490人,全部考生都完成体温检测需要20.25分钟.
23.如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣12)2+h,小明罚任意球时防守队员站在小明正前方9m处组成人墙,防守队员的身高为2.1m,对手球门与小明的水平距离为18m,已知足球球门高为2.43m.假定小明罚出的任意球恰好射正对手球门.
(1)当h=3时,求y与x的关系式;
(2)当h=3时,足球能否越过人墙?足球会不会踢飞?请说明理由;
(3)若小明罚出的任意球一定能直接射进对手球门得分,求h的取值范围.
解:(1)当h=3时,y=a(x﹣12)2+3,
∵抛物线y=a(x﹣12)2+3经过点(0,0),
∴0=a(0﹣12)2+3,
解得:a=﹣,
∴y与x的关系式y=﹣(x﹣12)2+3(0≤x≤24);
(2)当h=3时,足球能越过人墙,足球不会踢飞,理由如下:
当h=3时,由(1)得y=﹣(x﹣12)2+3,
当x=9时,y=﹣(9﹣12)2+3≈2.81>2.1,
∴足球能过人墙,
当x=18时,y=﹣(18﹣12)2+3=2.25<2.43,
∴足球能直接射进球门;
(3)由题设知y=a(x﹣12)2+h,函数图象过点(0,0),
得0=a(0﹣12)2+h,即144a+h=0①,
由足球能越过人墙,得9a+h>2.1②,
由足球能直接射进球门,得0<36a+h<2.43③,
由①得a=﹣④,
把④代入②得9×(﹣)+h>2.1,
解得h>2.24,
把④代入③得0<36×(﹣)+h<2.43,
解得0<h<3.24,
∴h的取值范围是2.24<h<3.24.
24.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为x米,与湖面的垂直高度为y米.下面的表中记录了x与y的五组数据:
x(米) 0 1 2 3 4
y(米) 0.5 1.25 1.5 1.25 0.5
(1)在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示y与x函数关系的图象;
(2)求y与x函数表达式;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).
解:(1)以喷泉与湖面的交点为原点,喷泉所在的直线为纵轴建立平面直角坐标系,如图1所示:
(2)根据图象可设二次函数的解析式为:y=a(x﹣2)2+1.5,
将(0,0.5)代入y=a(x﹣2)2+1.5,
解得a=﹣,
∴抛物线的解析式为:y=﹣x2+x+0.5;
(3)设调节后的水管喷出的抛物线的解析式为:y=﹣x2+x+0.5+n,
由题意可知,当横坐标为2+=时,纵坐标的值不小于2+0.5=2.5,
∴﹣×()2++0.5+n≥2.5,
解得n≥,
∴水管高度至少向上调节米,
∴0.5+≈2.1(米),
∴公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到约2.1米才能符合要求.
25.某公司生产的某种时令商品每件成本为20元,经过市场调研发现:
①这种商品在未来40天内的日销售量m(件)与时间t(天)的关系为:m=﹣2t+96.
②未来40天内,该商品每天的单价y(元/件)与时间t(天)(t为整数)之间关系的函数图象如图所示.
请结合上述信息解决下列问题:
(1)经计算得,当0<t≤20时,y关于t的函数关系式为 y=t+25 ;则当20<t≤40时,y关于t的函数关系式为 y=﹣t+40 .
(2)请预测未来40天中哪一天的单价是27元?
(3)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
解:(1)当0<t≤20时,y关于t的函数关系式为y=mt+n,
则,
解得,
∴y关于t的函数关系式为:y=t+25;
当20<t≤40时,y关于t的函数关系式为y=at+b,
则,
解得,
∴y关于t的函数关系式为:y=﹣t+40;
故答案为:y=t+25;y=﹣t+40;
(2)①当0<t≤20时,
令t+25=27,
解得t=8,
②当20<t≤40时,
令﹣t+40=27,
解得:t=26,
∴未来40天中第8天和第26天的单价是27元;
(3)前20天的销售利润为P1元,后20天的销售利润为P2元,
则P1=(﹣2t+96)(t+25﹣20)
=﹣(t﹣14)2+578,
∵﹣<0,
∴当t=14时,P1有最大值,为578元;
P2=(﹣2t+96)(﹣t+40﹣20)
=t2﹣88t+1920
=(t﹣44)2﹣16,
∵1>0,
∴当21≤t≤40时,P2随t的增大而减小,
∴当t=21时,P2最大,为513元,
∴第14天利润最大,最大利润为578元.
同课章节目录
