解直角三角形1[下学期]
文档属性
| 名称 | 解直角三角形1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 724.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-23 11:09:00 | ||
图片预览



文档简介
课件11张PPT。解直角三角形(一)要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:(1)使用这个梯子最高可以安全攀上多高的平房?(精确到0.1m)这个问题归结为:
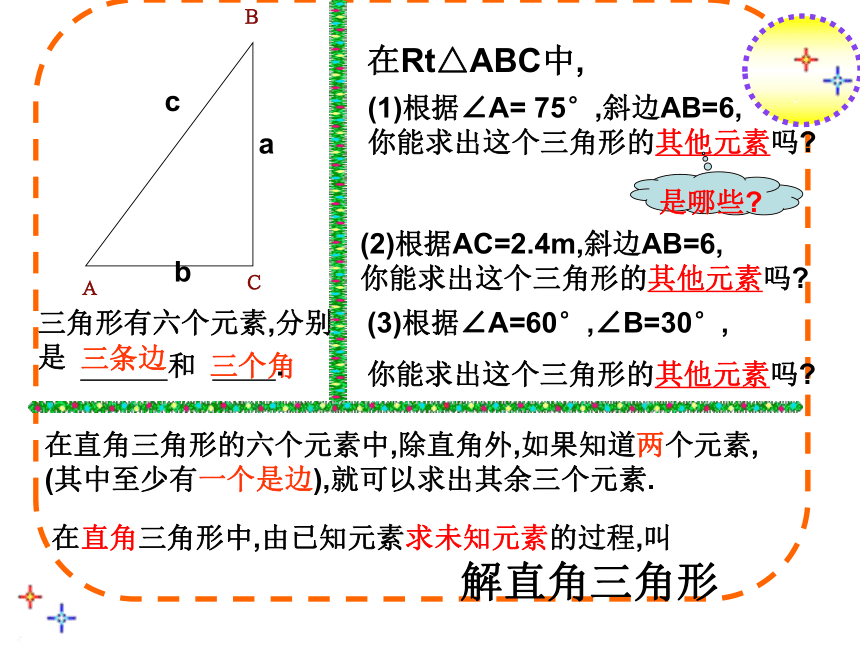
在Rt△ABC中,已知∠A= 75°,斜边AB=6,求BC的长角α越大,攀上的高度就越高.你能解决吗?要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?这个问题归结为: 在Rt△ABC中,已知AC=2.4m,斜边AB=6, 求锐角α的度数? 你能解决吗?角α是否在50°≤ α ≤75°内在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),就可以求出其余三个元素.三条边三个角在Rt△ABC中,(1)根据∠A= 75°,斜边AB=6,
你能求出这个三角形的其他元素吗?(2)根据AC=2.4m,斜边AB=6,
你能求出这个三角形的其他元素吗?(3)根据∠A=60°,∠B=30°,
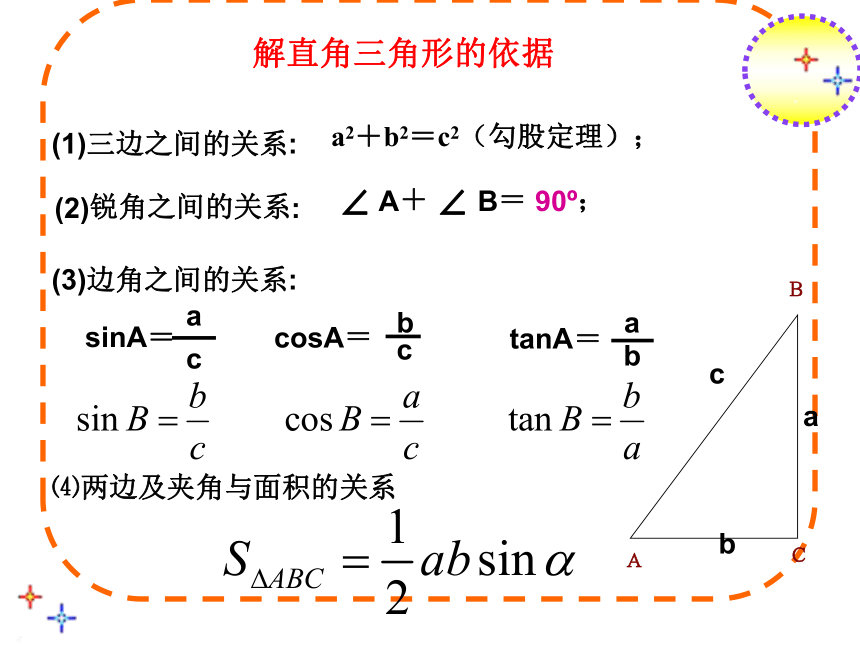
你能求出这个三角形的其他元素吗?在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形是哪些?(1)三边之间的关系:a2+b2=c2(勾股定理);解直角三角形的依据(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:⑷两边及夹角与面积的关系知道是求什么吗?解:知道是求什么吗?例2.在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形.(精确到0.1)解:回顾巩固练习在Rt△ABC中,∠C=90°,根据下列条件解直角三角形(1) a=30 ,b=20(2)∠B=72°, c=14解:过A作AD⊥BC于D设CD=x,在Rt△ACD中,得在Rt△ABD中,得 2. 如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?解 利用勾股定理可以求出折断倒下部分的长度为:26+10=36(米)答:大树在折断之前高为36米.回顾课堂小结⑴把实际问题转化成直角三角形来解决⑵怎样来解直角三角形及需要的知识⑶你还有什么收获…… ……(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:⑷两边及夹角与面积的关系
在Rt△ABC中,已知∠A= 75°,斜边AB=6,求BC的长角α越大,攀上的高度就越高.你能解决吗?要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?这个问题归结为: 在Rt△ABC中,已知AC=2.4m,斜边AB=6, 求锐角α的度数? 你能解决吗?角α是否在50°≤ α ≤75°内在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),就可以求出其余三个元素.三条边三个角在Rt△ABC中,(1)根据∠A= 75°,斜边AB=6,
你能求出这个三角形的其他元素吗?(2)根据AC=2.4m,斜边AB=6,
你能求出这个三角形的其他元素吗?(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗?在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形是哪些?(1)三边之间的关系:a2+b2=c2(勾股定理);解直角三角形的依据(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:⑷两边及夹角与面积的关系知道是求什么吗?解:知道是求什么吗?例2.在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形.(精确到0.1)解:回顾巩固练习在Rt△ABC中,∠C=90°,根据下列条件解直角三角形(1) a=30 ,b=20(2)∠B=72°, c=14解:过A作AD⊥BC于D设CD=x,在Rt△ACD中,得在Rt△ABD中,得 2. 如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?解 利用勾股定理可以求出折断倒下部分的长度为:26+10=36(米)答:大树在折断之前高为36米.回顾课堂小结⑴把实际问题转化成直角三角形来解决⑵怎样来解直角三角形及需要的知识⑶你还有什么收获…… ……(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:⑷两边及夹角与面积的关系
