解直角三角形(2)[下学期]
文档属性
| 名称 | 解直角三角形(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 445.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-14 00:00:00 | ||
图片预览


文档简介
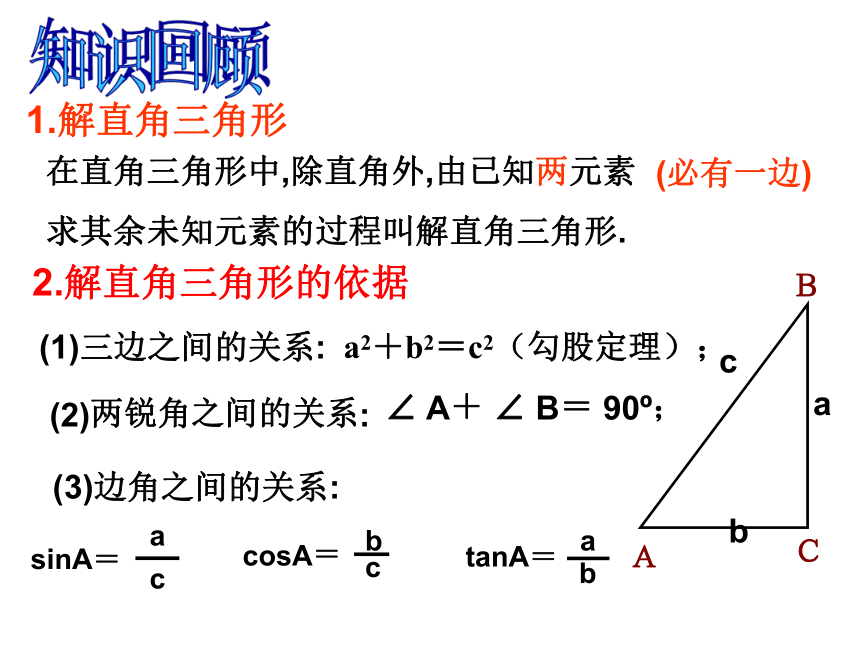
课件18张PPT。解直角三角形的应用(1)在直角三角形中,除直角外,由已知两元素
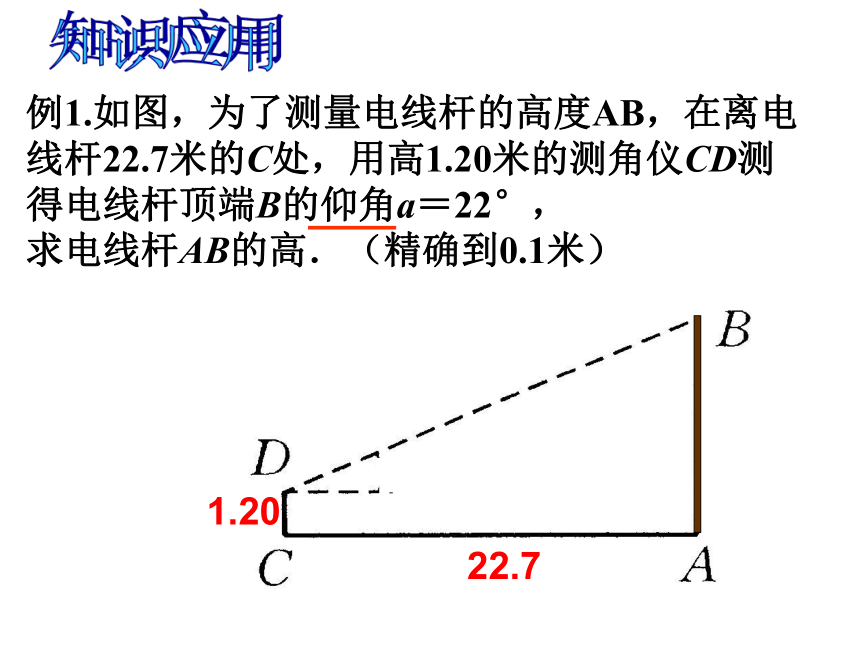
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
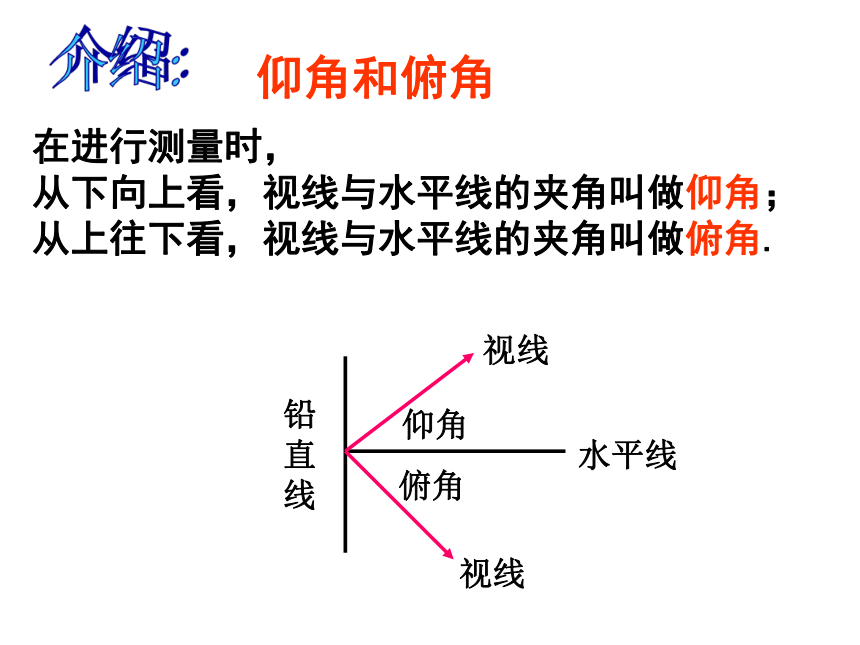
求电线杆AB的高.(精确到0.1米)1.2022.7知识应用仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
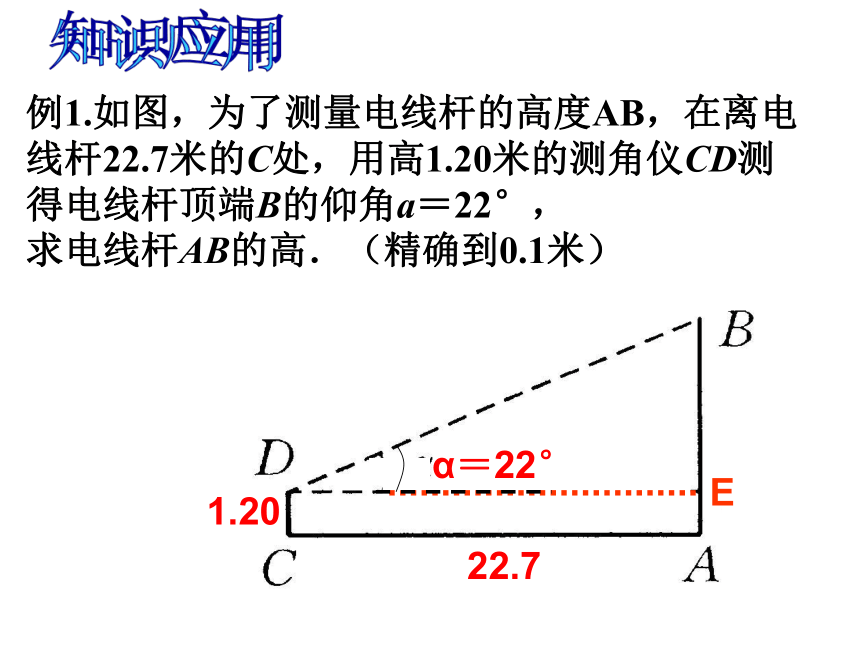
介绍:例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
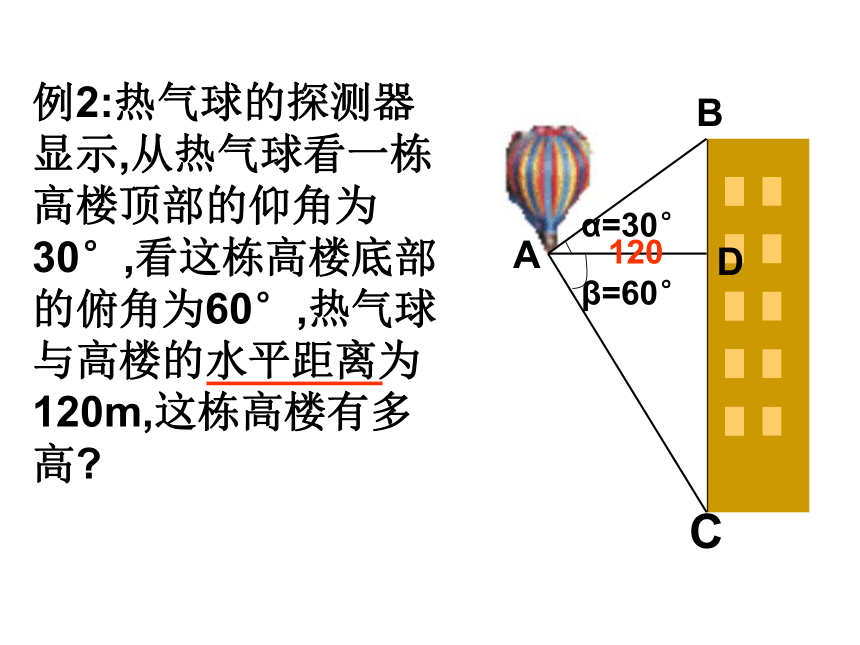
求电线杆AB的高.(精确到0.1米)1.2022.7α=22°知识应用E练习:升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰好30°,若双眼离地面1.5米,则旗杆高度为_________米.(用含根号的式子表示)例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD巩固练习1.如图,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得点C的俯角为β,则较低建筑物CD的高为_______米ABCD巩固练习2.如图,在C处测得旗杆A的仰角为30°,向前进10米到达D处,在D处测得A的仰角为45°,则旗杆的高为______米.CDBA30°1045°巩固练习3.建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)40(课本93页)利用解直角三角形的知识解决实际问题的
一般过程是:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)65°34°PBCA指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
方位角介绍:例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)65°34°PBCA80例4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BADF60°1230°巩固练习A城气象台测得一热带风暴中心从城正西方向300处以每小时26km的速度向北偏东60°方向移动,距风暴中心200km的范围内为受影响区域. (1)A城是否受这次风暴影响?为什么? (2)若A城受这次风暴影响,那么影响的时间多长(精确到1时)?北东O.AM60° 1.在解直角三角形及应用时经常接触到的一些概念(仰角,俯角;方位角等)
2.实际问题向数学模型的转化
(解直角三角形)
知识小结再见
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
求电线杆AB的高.(精确到0.1米)1.2022.7知识应用仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
介绍:例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
求电线杆AB的高.(精确到0.1米)1.2022.7α=22°知识应用E练习:升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰好30°,若双眼离地面1.5米,则旗杆高度为_________米.(用含根号的式子表示)例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD巩固练习1.如图,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得点C的俯角为β,则较低建筑物CD的高为_______米ABCD巩固练习2.如图,在C处测得旗杆A的仰角为30°,向前进10米到达D处,在D处测得A的仰角为45°,则旗杆的高为______米.CDBA30°1045°巩固练习3.建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)40(课本93页)利用解直角三角形的知识解决实际问题的
一般过程是:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)65°34°PBCA指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
方位角介绍:例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)65°34°PBCA80例4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BADF60°1230°巩固练习A城气象台测得一热带风暴中心从城正西方向300处以每小时26km的速度向北偏东60°方向移动,距风暴中心200km的范围内为受影响区域. (1)A城是否受这次风暴影响?为什么? (2)若A城受这次风暴影响,那么影响的时间多长(精确到1时)?北东O.AM60° 1.在解直角三角形及应用时经常接触到的一些概念(仰角,俯角;方位角等)
2.实际问题向数学模型的转化
(解直角三角形)
知识小结再见
