解直角三角形的应用[上学期]
文档属性
| 名称 | 解直角三角形的应用[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 130.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-13 00:00:00 | ||
图片预览




文档简介
课件14张PPT。年级科目:初三几何
课 题:解直角三角形的应用
单 位:宁陵县实验中学
授课教师:张 艳1、什么叫解直角三角形? 由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。2、直角三角形(除直角外)五元素的关系是什么?(2)锐角之间的关系
∠A + ∠B = 900 (1)三边之间的关系
a2 + b2 = c2 (勾股定理) (3)边角之间的关系
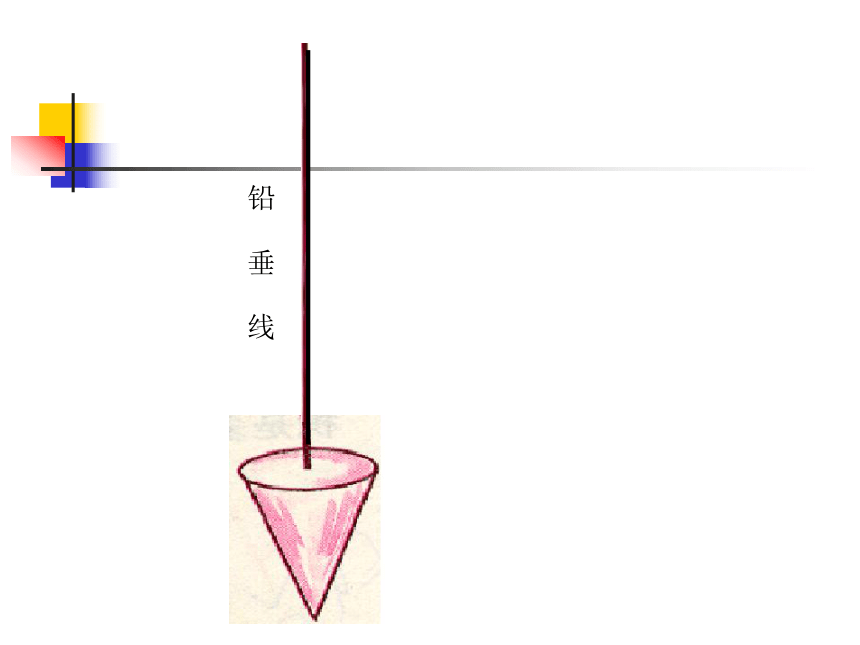
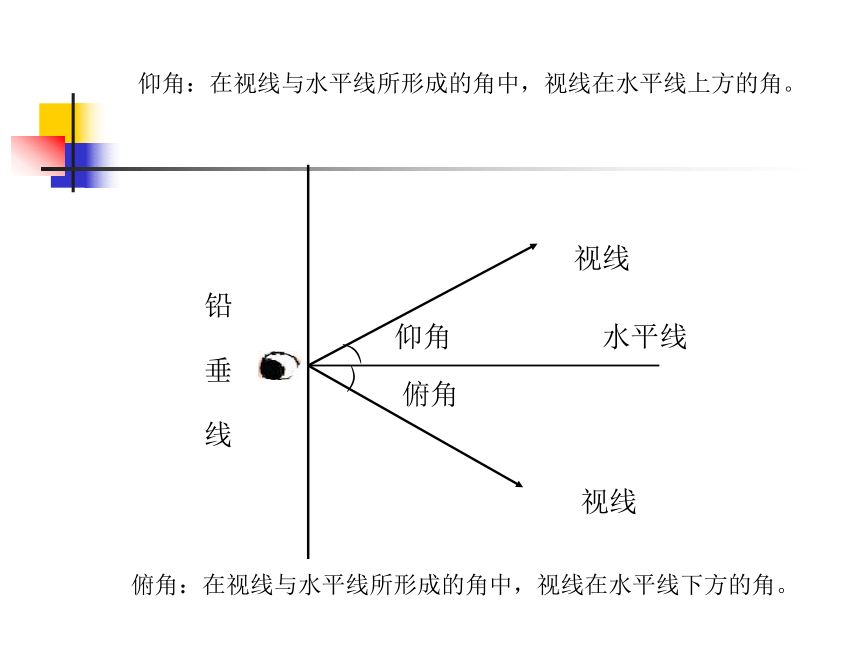
tanA cotA 铅 垂 线水平线视线视线︶仰角俯角铅 垂 线仰角:在视线与水平线所形成的角中,视线在水平线上方的角。俯角:在视线与水平线所形成的角中,视线在水平线下方的角。︶︶例1 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α =16°31′,求飞机A到控制点B的距离(精确到1米)。 解: 在Rt ⊿ABC中,sinB = , ∴ AB = = ≈4221(米).Aa1200米16°31′答:飞机A到控制点B的距离约为4221米.BC 例2 如图,某海岛上的观察所A发现海上某船只B 并测得其俯角α=30o。已知观察所A的标高(当水位为0 m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m) ABC︶a30o443.74+3.74 例2 如图,某海岛上的观察所A发现海上某船只B 并测得其俯角α=30o。已知观察所A的标高(当水位为0 m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m) 解:在Rt ⊿ABC中 , cot B= ,答:观察所A到船只B的水平距离BC为762m. ∴ BC= AC? cot B =(443.74-3.74)? cot30°
=440.00? 1.732
≈762 (m). 练习 某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°。求铁塔AB高。(精确到0. 1米)330米ABCDEα︶︶a1、有关概念:仰角、俯角、标高、水位2、用解直角三角形知识解决此类问题的一般步骤:(1)通过读题把实物图转化为数学图形;(2)找出来有关直角三角形和已知、未知元素;(3)选合适的锐角函数关系求未知数;(4)答小结:
课 题:解直角三角形的应用
单 位:宁陵县实验中学
授课教师:张 艳1、什么叫解直角三角形? 由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。2、直角三角形(除直角外)五元素的关系是什么?(2)锐角之间的关系
∠A + ∠B = 900 (1)三边之间的关系
a2 + b2 = c2 (勾股定理) (3)边角之间的关系
tanA cotA 铅 垂 线水平线视线视线︶仰角俯角铅 垂 线仰角:在视线与水平线所形成的角中,视线在水平线上方的角。俯角:在视线与水平线所形成的角中,视线在水平线下方的角。︶︶例1 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α =16°31′,求飞机A到控制点B的距离(精确到1米)。 解: 在Rt ⊿ABC中,sinB = , ∴ AB = = ≈4221(米).Aa1200米16°31′答:飞机A到控制点B的距离约为4221米.BC 例2 如图,某海岛上的观察所A发现海上某船只B 并测得其俯角α=30o。已知观察所A的标高(当水位为0 m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m) ABC︶a30o443.74+3.74 例2 如图,某海岛上的观察所A发现海上某船只B 并测得其俯角α=30o。已知观察所A的标高(当水位为0 m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m) 解:在Rt ⊿ABC中 , cot B= ,答:观察所A到船只B的水平距离BC为762m. ∴ BC= AC? cot B =(443.74-3.74)? cot30°
=440.00? 1.732
≈762 (m). 练习 某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°。求铁塔AB高。(精确到0. 1米)330米ABCDEα︶︶a1、有关概念:仰角、俯角、标高、水位2、用解直角三角形知识解决此类问题的一般步骤:(1)通过读题把实物图转化为数学图形;(2)找出来有关直角三角形和已知、未知元素;(3)选合适的锐角函数关系求未知数;(4)答小结:
