人教版2005年广东地区数学科解直角三角形复习课课件[下学期]
文档属性
| 名称 | 人教版2005年广东地区数学科解直角三角形复习课课件[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-18 22:07:00 | ||
图片预览




文档简介
课件14张PPT。解直角三角形复习课
引例:
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42m,你能根据这些条件求出文光塔的高度吗?ABCabc小结:在Rt△ABC中,∠ C为直角, ∠ A, ∠ B为锐角,它们所对的边分别为a、b、c,其中除直角外,其余的五个元素有以下关系:
a2+b2=c2∠A+∠B=900 三边之间的关系:角角之间的关系:边角之间的关系:sinA= = cosB cosA= =sinB
tanA= = cotB cotA= =tanB AC=_________, ∠A=_________45°则AB=__________,1、解直角三角形的概念
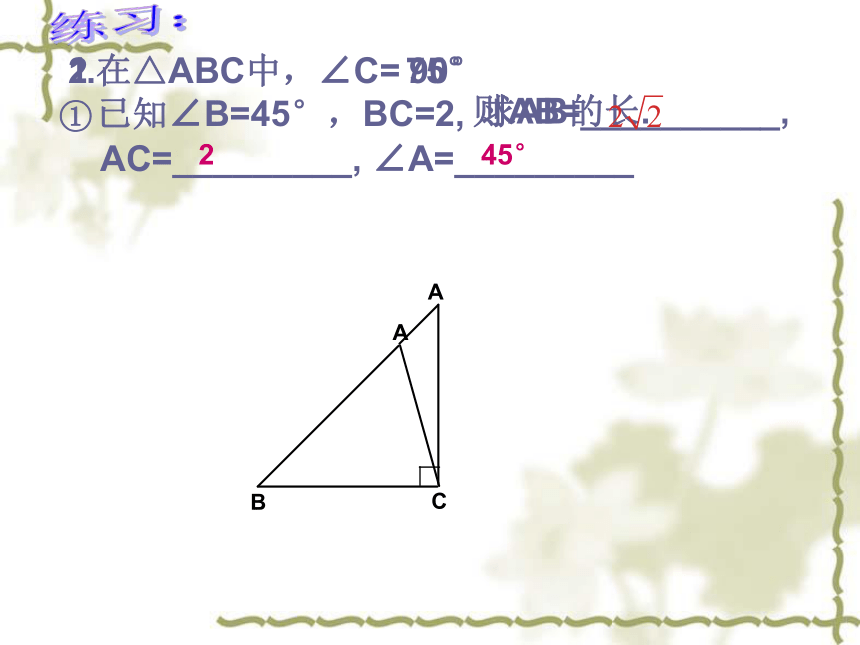
在直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。1.在△ABC中,∠C=
已知∠B=45°,BC=2, 90°②已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2、直角三角形的解法:
已知直角三角形的2个元素(至少有1个是边),利用直角三角形的元素间的关系,可以求出其余的3个元素。③已知∠A=30°,∠B=60°,那么AB=__, BC=__,AC=__2160°30°练习:① 22求AB的长. .在△ABC中,∠C=
已知∠B=45°,BC=2, ① 90°75°练习:12 AC=_________, ∠A=_________45°则AB=__________,2
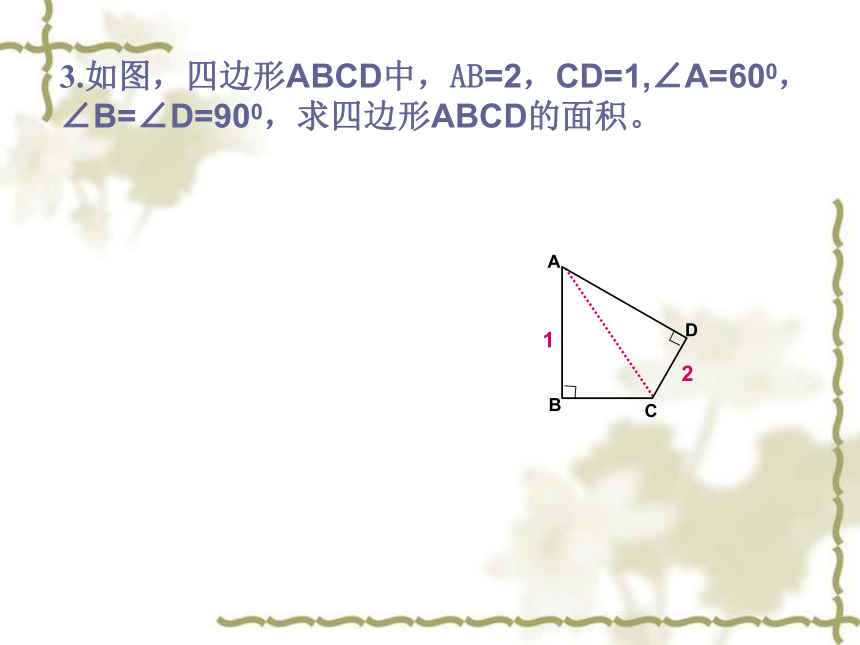
3.如图,四边形ABCD中,AB=2,CD=1,∠A=600,∠B=∠D=900,求四边形ABCD的面积。∟∟21
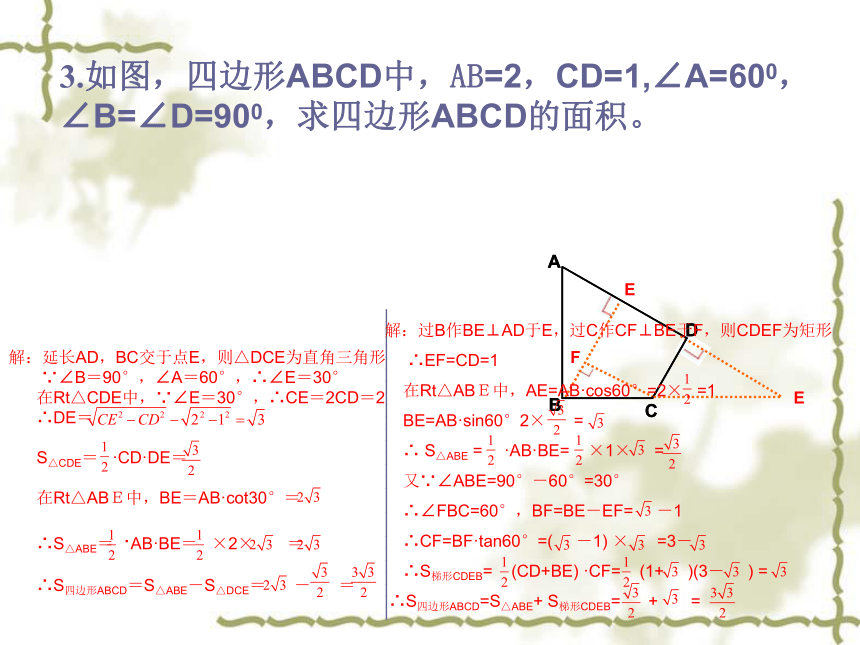
3.如图,四边形ABCD中,AB=2,CD=1,∠A=600,∠B=∠D=900,求四边形ABCD的面积。__________________________解:延长AD,BC交于点E,则△DCE为直角三角形
∵∠B=90°,∠A=60°,∴∠E=30°
在Rt△CDE中,∵∠E=30°,∴CE=2CD=2
∴DE=
S△CDE= ·CD·DE=
在Rt△ABE中,BE=AB·cot30°=
∴S△ABE= ·AB·BE= ×2× =
∴S四边形ABCD=S△ABE-S△DCE= - =解:过B作BE⊥AD于E,过C作CF⊥BE于F,则CDEF为矩形
∴EF=CD=1
在Rt△ABE中,AE=AB·cos60°=2× =1
BE=AB·sin60°2× =
∴ S△ABE = ·AB·BE= ×1× =
又∵∠ABE=90°-60°=30°
∴∠FBC=60°,BF=BE-EF= -1
∴CF=BF·tan60°=( -1) × =3-
∴S梯形CDEB= (CD+BE) ·CF= (1+ )(3- ) =
∴S四边形ABCD=S△ABE+ S梯形CDEB= + =
4.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42m,请根据这些条件求出文光塔的高度。(供选用数据:sin64°=0.8988, cos64°=0.4384, tan64°=2.050, cot64°=0.4877.
精确到0.1m)⌒64°解:过A作正东方向的垂线,垂足为B
在Rt△AOB中,OA=4200,∠AOB=90°-74°=16°
AB=OA·sin∠AOB
=4200·sin16°
=4200·cos74°
=4200×0.2756
≈1158(米)>1000(米)
答:此艇按原航向继续航行没有触礁的危险。能力提高: 5.如图,灯塔A周围1000米处水域内有礁石,一船艇由西向东航行,在O处测得灯在北偏东740方向线上,这时O、A相距4200米,如果不改变航行方向,此艇是否有触礁的危险?(供选用的数据:cos740=0.2756,sin740=0.9613,cot740=0.2867,tan740=3.487。精确到1米)OA知一边一锐角解直角三角形知两边解直角三角形非直角三角形:添设辅助线转化为
解直角三角形解直角三角形三角形解直角总结:课外练习:1.在△ABC中,∠C=90°,sinA= ,D为AC上一点,∠BDC=45°,DC=6,求AB的长。 2.山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α =600,杆底C的俯角β =450,已知旗杆高BC=20米, 求山高CD。(保留三个有效数字)图13、在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,斜度线与地板的夹角为倾角θ,一般情况下,倾角θ愈小,楼梯的安全程度愈高。如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角为θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,θ1=45°θ2=30°求楼梯占用地板的长度增加了多少?(精确到0.01, =1.732)?多谢光临指导
引例:
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42m,你能根据这些条件求出文光塔的高度吗?ABCabc小结:在Rt△ABC中,∠ C为直角, ∠ A, ∠ B为锐角,它们所对的边分别为a、b、c,其中除直角外,其余的五个元素有以下关系:
a2+b2=c2∠A+∠B=900 三边之间的关系:角角之间的关系:边角之间的关系:sinA= = cosB cosA= =sinB
tanA= = cotB cotA= =tanB AC=_________, ∠A=_________45°则AB=__________,1、解直角三角形的概念
在直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。1.在△ABC中,∠C=
已知∠B=45°,BC=2, 90°②已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2、直角三角形的解法:
已知直角三角形的2个元素(至少有1个是边),利用直角三角形的元素间的关系,可以求出其余的3个元素。③已知∠A=30°,∠B=60°,那么AB=__, BC=__,AC=__2160°30°练习:① 22求AB的长. .在△ABC中,∠C=
已知∠B=45°,BC=2, ① 90°75°练习:12 AC=_________, ∠A=_________45°则AB=__________,2
3.如图,四边形ABCD中,AB=2,CD=1,∠A=600,∠B=∠D=900,求四边形ABCD的面积。∟∟21
3.如图,四边形ABCD中,AB=2,CD=1,∠A=600,∠B=∠D=900,求四边形ABCD的面积。__________________________解:延长AD,BC交于点E,则△DCE为直角三角形
∵∠B=90°,∠A=60°,∴∠E=30°
在Rt△CDE中,∵∠E=30°,∴CE=2CD=2
∴DE=
S△CDE= ·CD·DE=
在Rt△ABE中,BE=AB·cot30°=
∴S△ABE= ·AB·BE= ×2× =
∴S四边形ABCD=S△ABE-S△DCE= - =解:过B作BE⊥AD于E,过C作CF⊥BE于F,则CDEF为矩形
∴EF=CD=1
在Rt△ABE中,AE=AB·cos60°=2× =1
BE=AB·sin60°2× =
∴ S△ABE = ·AB·BE= ×1× =
又∵∠ABE=90°-60°=30°
∴∠FBC=60°,BF=BE-EF= -1
∴CF=BF·tan60°=( -1) × =3-
∴S梯形CDEB= (CD+BE) ·CF= (1+ )(3- ) =
∴S四边形ABCD=S△ABE+ S梯形CDEB= + =
4.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42m,请根据这些条件求出文光塔的高度。(供选用数据:sin64°=0.8988, cos64°=0.4384, tan64°=2.050, cot64°=0.4877.
精确到0.1m)⌒64°解:过A作正东方向的垂线,垂足为B
在Rt△AOB中,OA=4200,∠AOB=90°-74°=16°
AB=OA·sin∠AOB
=4200·sin16°
=4200·cos74°
=4200×0.2756
≈1158(米)>1000(米)
答:此艇按原航向继续航行没有触礁的危险。能力提高: 5.如图,灯塔A周围1000米处水域内有礁石,一船艇由西向东航行,在O处测得灯在北偏东740方向线上,这时O、A相距4200米,如果不改变航行方向,此艇是否有触礁的危险?(供选用的数据:cos740=0.2756,sin740=0.9613,cot740=0.2867,tan740=3.487。精确到1米)OA知一边一锐角解直角三角形知两边解直角三角形非直角三角形:添设辅助线转化为
解直角三角形解直角三角形三角形解直角总结:课外练习:1.在△ABC中,∠C=90°,sinA= ,D为AC上一点,∠BDC=45°,DC=6,求AB的长。 2.山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α =600,杆底C的俯角β =450,已知旗杆高BC=20米, 求山高CD。(保留三个有效数字)图13、在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,斜度线与地板的夹角为倾角θ,一般情况下,倾角θ愈小,楼梯的安全程度愈高。如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角为θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,θ1=45°θ2=30°求楼梯占用地板的长度增加了多少?(精确到0.01, =1.732)?多谢光临指导
