解直角三角形.01[上学期]
文档属性
| 名称 | 解直角三角形.01[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-07-18 00:00:00 | ||
图片预览








文档简介
课件22张PPT。解直角三角形高密市城南中学
李宗洲(说课案例)标注
点击每页幻灯片的 图标,则幻灯片翻页一 教材分析单元知识内容:
1 直角三角形的边角关系.
2 应用勾股定理、 Rt△的两锐角互余及锐角三角函数解直角三角形.
3 应用解直角三角形的有关知识解决一些简单的实际问题(包括完成实习作业).二教学目标 1 掌握直角三角形的边角关系.
2 灵活运用勾股定理、直角三角形的两锐角互余及锐角 三角函数解直角三角形.
3 会用解直角三角形的有关知识解某些简单的实 际问题;完成简单的实习作业.
4 进一步提高学生数形结合、分析问题以及解决实际问题的能力和应用数学知识的意识;树立理论来源于实践又应用于实践的辨证唯主义观点.三 教学方法现代教育媒体手段下的数形结合、启发诱导、理论联系实际的教学方法重点:准确作辅助线并选择适当的关系解直角三角形;把实际问题转化为数学问题.难点:直角三角形的解法及其实际应用.四 重点、难点及突破 措施突破措施1 让学生牢记解直角三角形的条件和直角三角形三边间、边角间的关系及其变形.
2 在解题前,明确那些是已知元素、那些是未知元素以及它们的因果关系.例1 在Rt△ ABC中,c=20,A=420,解这个三角形
例2 在Rt△ ABC中,已知b=35,c=45,解这个三角形
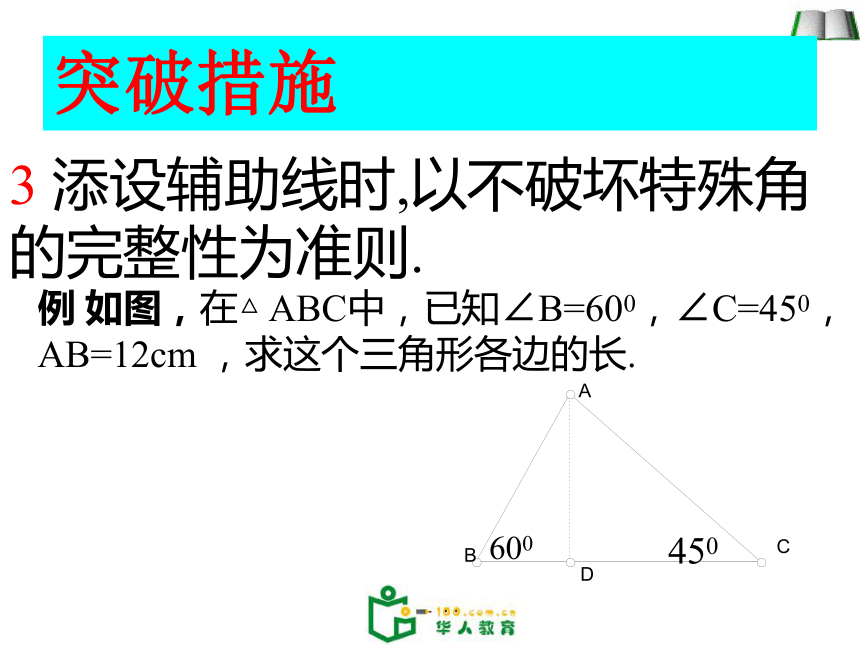
3 添设辅助线时,以不破坏特殊角的完整性为准则.突破措施例 如图,在△ ABC中,已知∠B=600,∠C=450,AB=12cm ,求这个三角形各边的长. 4506004 数形结合,从观察中进行、
分析、转化、解答.例 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.α突破措施例 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山?
5 利用学生感兴趣的实际问题, 进行突破、学习.突破措施6 充分利用活动课进行实习训练,让学生在愉快的情景中接受知识.例题 某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.ABDC300450例 学生利用自制的测倾器测 我校 旗杆、教学楼的高度.五 课型及课时安排课 型: 新授课 复习课 习题课 测评课 活动课 解直角三角形 2课时
解直角三角形
的应用举例 5课时
新授课复习课 1课时
课时安排:
习题课 1课时 测评课 2课时活动课 2课时六 单元知识网络直角三角形的边角关系解直角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形知一斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用抽象出图形,再添设辅助线求解直接抽象出直角三角形解直角三角形实习作业1 在直角三角形ABC中,已知C=90,∠A、∠B、∠C的对边分别是a、b、c,则
(1) a、b、c满足怎样的关系式:
(2) 锐角A、B满足怎样的关系式:
(3) 仿照下表第二行填空
2 分别写出300、450、600、900四个角的三角函数值七 单元训练设计(一)前置测评(二)新授课强化训练题组二 解直角三角形的实际应用
1 教科书P45第1题 2 教科书P45第2题
3 教科书P52第2题 4 教科书P51第2题
5 教科书P51第3题
一 解直角三角形
1 教科书P42第2题
2 教科书P41第2题、P42第3—7题
(三)活动课作业 教科书P57实习作业(物体:城南邮电局的发射塔)
(目标1) 1 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
2 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
(目标2) 3 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
4 山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,坡度是
5如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得CD=100米
设山高AB=x则列 出关于X的方程是 解得x=
(目标3) 6湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,
又测得气球在湖中的俯角为β试求气球距湖面的高度h.
7我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶
的 水平距离 为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,
试问:它能部能通过这座小?
(四) 复习题(五)单元达标测试题一 选择题
1 在下列直角三角形中,不能求出解的水( )
A 已知一直角边和所对的角 B 已知两个锐角
C 已知斜边和一个锐角 D 已知两直角边
(目标1) 2 在Rt△ABC中,∠C=900,cosB=2/3,则 a:b:c=( )
A 2:√5:3 B 1:√2:√3 C 2:√5:√3 D 1:2:3
3 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
4 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
(目标2) 5 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
6 在等腰△ ABC中,顶角为锐角,一腰上的高线为1 ,这条高线与
另一腰的夹角为450,则三角形ABC的面积为()
A√2/2 B √3 C 1/2 D 1/4 二 填空题
(目标1) 1 在在Rt△ABC中, ∠C=900,如果已知b和∠A,则a=
c= (用锐角三角函数表示)
(目标2) 2在△ ABC中,C =900,A=600,a+b=3+√3,则c=
3 山坡与地面成300的倾斜角,某人上坡走60米,则他
(目标3) 上升 米,坡度是
4 如图已知堤坝的横断面为梯形,AD坡面的水平宽度为
3√3米,DC=4米,B=600,则
(1)斜坡AD 的铅直高度是
(2)斜坡AD 的长是 (3)坡角A的度数是
(4)堤坝底AB的长是 (5)斜坡BC的长是i=1:√3(目标3) 6 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,
测得 CD=100米,设山高AB=x则列出关于X的方程是
解得x=
三 解答题
(目标2) 1在在Rt△ABC中, ∠C=900,a+b=12,
tgB=2,求C的值及∠ABD的度数
(目标3) 2 山顶上有一座电视塔,在塔顶B处测得地面上
一点A的俯角=600,在塔底C处测得A的俯角
α=450,已知塔高为β=60米,求山高
(目标3)3 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知 山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山 ?αβ(目标3) 4 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
450600(目标3)四 探索题
湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,又测得气球在湖中的俯角为β试求气球距湖面的高度h.八 作业设计 1 教科书P45第1题 第2题
2 教科书P51第2题 P52第2题
3 教科书P51第2、3题
4 教科书P57实习作业
李宗洲(说课案例)标注
点击每页幻灯片的 图标,则幻灯片翻页一 教材分析单元知识内容:
1 直角三角形的边角关系.
2 应用勾股定理、 Rt△的两锐角互余及锐角三角函数解直角三角形.
3 应用解直角三角形的有关知识解决一些简单的实际问题(包括完成实习作业).二教学目标 1 掌握直角三角形的边角关系.
2 灵活运用勾股定理、直角三角形的两锐角互余及锐角 三角函数解直角三角形.
3 会用解直角三角形的有关知识解某些简单的实 际问题;完成简单的实习作业.
4 进一步提高学生数形结合、分析问题以及解决实际问题的能力和应用数学知识的意识;树立理论来源于实践又应用于实践的辨证唯主义观点.三 教学方法现代教育媒体手段下的数形结合、启发诱导、理论联系实际的教学方法重点:准确作辅助线并选择适当的关系解直角三角形;把实际问题转化为数学问题.难点:直角三角形的解法及其实际应用.四 重点、难点及突破 措施突破措施1 让学生牢记解直角三角形的条件和直角三角形三边间、边角间的关系及其变形.
2 在解题前,明确那些是已知元素、那些是未知元素以及它们的因果关系.例1 在Rt△ ABC中,c=20,A=420,解这个三角形
例2 在Rt△ ABC中,已知b=35,c=45,解这个三角形
3 添设辅助线时,以不破坏特殊角的完整性为准则.突破措施例 如图,在△ ABC中,已知∠B=600,∠C=450,AB=12cm ,求这个三角形各边的长. 4506004 数形结合,从观察中进行、
分析、转化、解答.例 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.α突破措施例 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山?
5 利用学生感兴趣的实际问题, 进行突破、学习.突破措施6 充分利用活动课进行实习训练,让学生在愉快的情景中接受知识.例题 某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.ABDC300450例 学生利用自制的测倾器测 我校 旗杆、教学楼的高度.五 课型及课时安排课 型: 新授课 复习课 习题课 测评课 活动课 解直角三角形 2课时
解直角三角形
的应用举例 5课时
新授课复习课 1课时
课时安排:
习题课 1课时 测评课 2课时活动课 2课时六 单元知识网络直角三角形的边角关系解直角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形知一斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用抽象出图形,再添设辅助线求解直接抽象出直角三角形解直角三角形实习作业1 在直角三角形ABC中,已知C=90,∠A、∠B、∠C的对边分别是a、b、c,则
(1) a、b、c满足怎样的关系式:
(2) 锐角A、B满足怎样的关系式:
(3) 仿照下表第二行填空
2 分别写出300、450、600、900四个角的三角函数值七 单元训练设计(一)前置测评(二)新授课强化训练题组二 解直角三角形的实际应用
1 教科书P45第1题 2 教科书P45第2题
3 教科书P52第2题 4 教科书P51第2题
5 教科书P51第3题
一 解直角三角形
1 教科书P42第2题
2 教科书P41第2题、P42第3—7题
(三)活动课作业 教科书P57实习作业(物体:城南邮电局的发射塔)
(目标1) 1 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
2 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
(目标2) 3 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
4 山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,坡度是
5如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得CD=100米
设山高AB=x则列 出关于X的方程是 解得x=
(目标3) 6湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,
又测得气球在湖中的俯角为β试求气球距湖面的高度h.
7我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶
的 水平距离 为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,
试问:它能部能通过这座小?
(四) 复习题(五)单元达标测试题一 选择题
1 在下列直角三角形中,不能求出解的水( )
A 已知一直角边和所对的角 B 已知两个锐角
C 已知斜边和一个锐角 D 已知两直角边
(目标1) 2 在Rt△ABC中,∠C=900,cosB=2/3,则 a:b:c=( )
A 2:√5:3 B 1:√2:√3 C 2:√5:√3 D 1:2:3
3 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
4 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
(目标2) 5 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
6 在等腰△ ABC中,顶角为锐角,一腰上的高线为1 ,这条高线与
另一腰的夹角为450,则三角形ABC的面积为()
A√2/2 B √3 C 1/2 D 1/4 二 填空题
(目标1) 1 在在Rt△ABC中, ∠C=900,如果已知b和∠A,则a=
c= (用锐角三角函数表示)
(目标2) 2在△ ABC中,C =900,A=600,a+b=3+√3,则c=
3 山坡与地面成300的倾斜角,某人上坡走60米,则他
(目标3) 上升 米,坡度是
4 如图已知堤坝的横断面为梯形,AD坡面的水平宽度为
3√3米,DC=4米,B=600,则
(1)斜坡AD 的铅直高度是
(2)斜坡AD 的长是 (3)坡角A的度数是
(4)堤坝底AB的长是 (5)斜坡BC的长是i=1:√3(目标3) 6 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,
测得 CD=100米,设山高AB=x则列出关于X的方程是
解得x=
三 解答题
(目标2) 1在在Rt△ABC中, ∠C=900,a+b=12,
tgB=2,求C的值及∠ABD的度数
(目标3) 2 山顶上有一座电视塔,在塔顶B处测得地面上
一点A的俯角=600,在塔底C处测得A的俯角
α=450,已知塔高为β=60米,求山高
(目标3)3 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知 山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山 ?αβ(目标3) 4 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
450600(目标3)四 探索题
湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,又测得气球在湖中的俯角为β试求气球距湖面的高度h.八 作业设计 1 教科书P45第1题 第2题
2 教科书P51第2题 P52第2题
3 教科书P51第2、3题
4 教科书P57实习作业
