第28章 解直角三角形跟踪训练检测题(含详细答案)[下学期]
文档属性
| 名称 | 第28章 解直角三角形跟踪训练检测题(含详细答案)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 144.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-03 18:31:00 | ||
图片预览

文档简介
跟踪训练检测题
(测试范围:28.2 解直角三角形)
天津市葛沽第三中学 李玉强 (300352)
一、选择题(每小题5分,共30分)
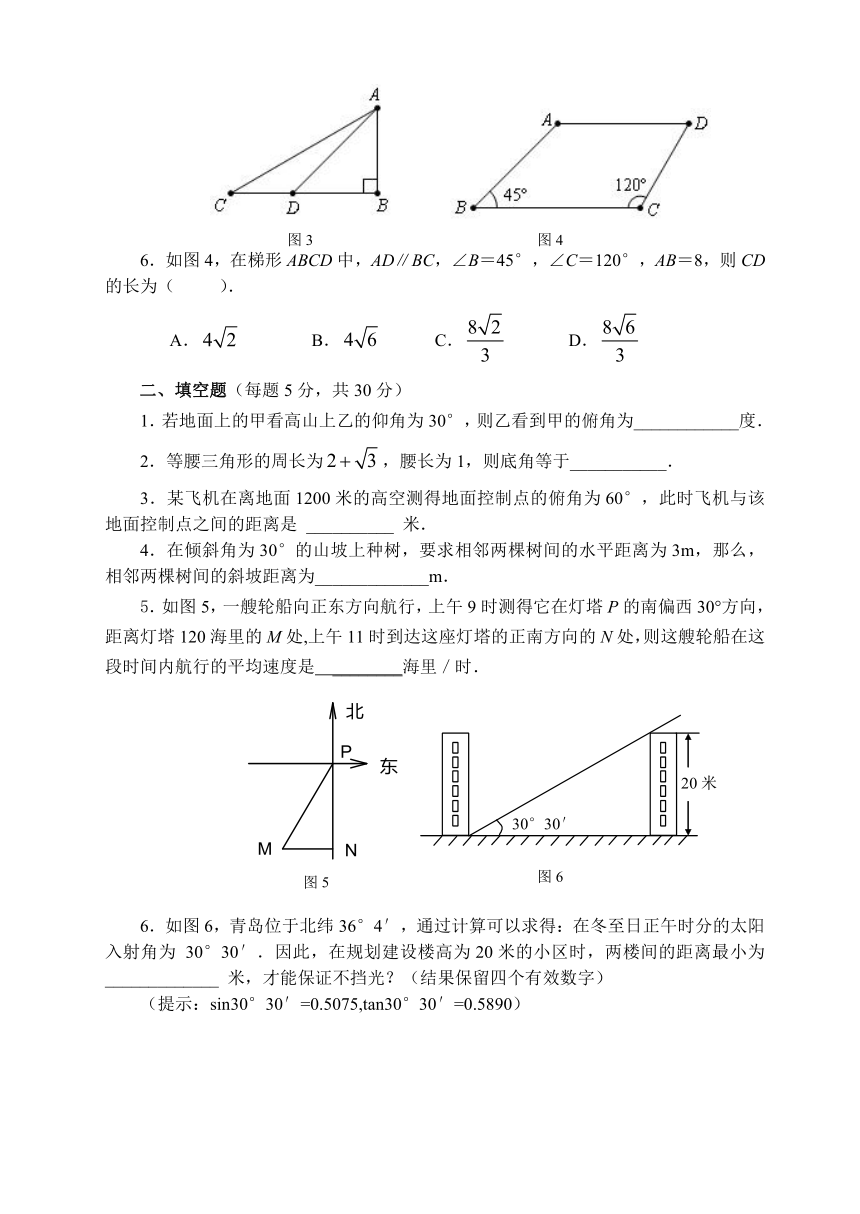
1.如图1,为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为,则楼房BC的高为( ).
A.30tan米 B.米 C.30sin米 D.米
2.如图2,两建筑物的水平距离为100米,从A点测得D点的俯角为,测得C点的俯角为,则较低建筑物的高为( )米.
A.100 B. C. D.
3.在Rt△ABC中,∠C=90°,cosA=,则tanA=( ).
A. B. C. D.24
4.等腰三角形顶角∠A=120°,高AD=30,则三角形的周长等于( ).
A. B. C. D.
5.如图3,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为( ).
A.m B.m
C.m D.m
6.如图4,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( ).
A. B. C. D.
二、填空题(每题5分,共30分)
1.若地面上的甲看高山上乙的仰角为30°,则乙看到甲的俯角为____________度.
2.等腰三角形的周长为,腰长为1,则底角等于___________.
3.某飞机在离地面1200米的高空测得地面控制点的俯角为60°,此时飞机与该地面控制点之间的距离是 __________ 米.
4.在倾斜角为30°的山坡上种树,要求相邻两棵树间的水平距离为3m,那么,相邻两棵树间的斜坡距离为_____________m.
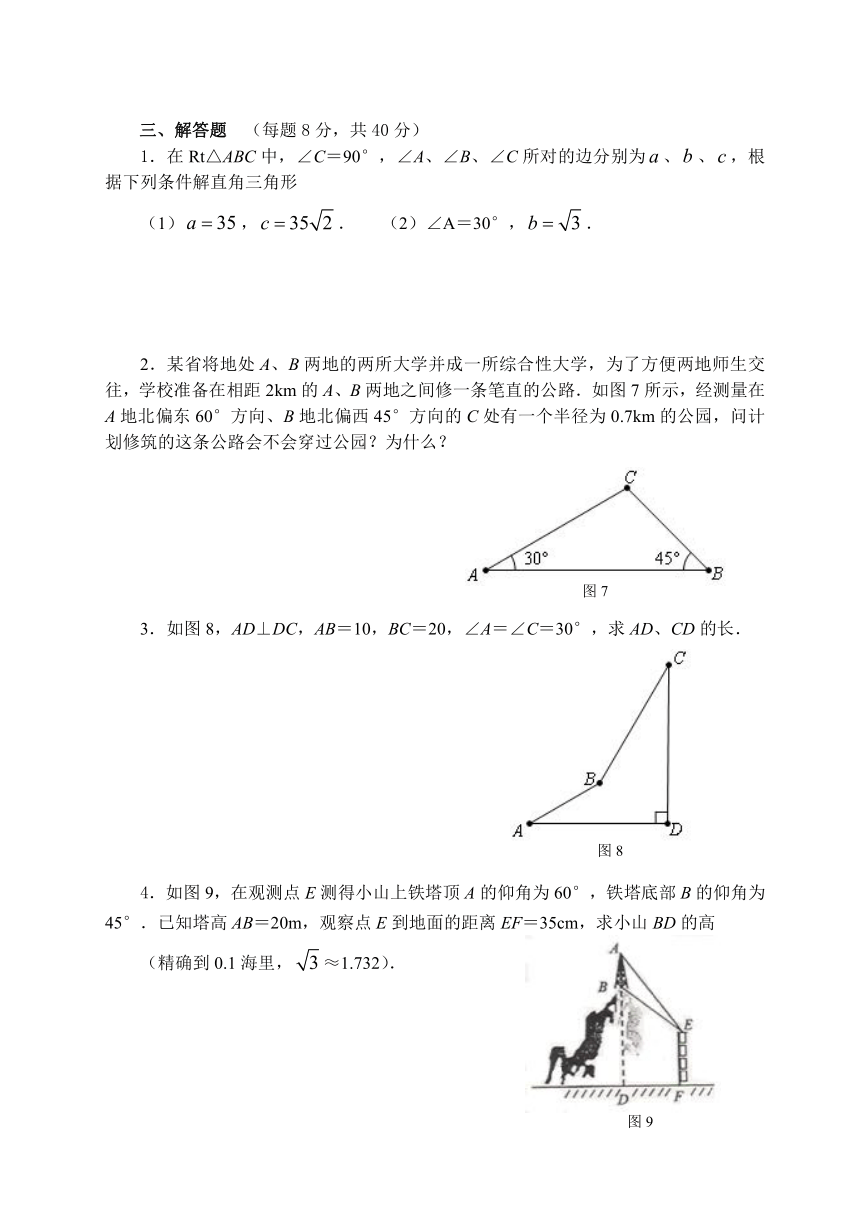
5.如图5,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是 ________海里/时.
6.如图6,青岛位于北纬36°4′,通过计算可以求得:在冬至日正午时分的太阳入射角为 30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小为_____________ 米,才能保证不挡光?(结果保留四个有效数字)
(提示:sin30°30′=0.5075,tan30°30′=0.5890)
三、解答题 (每题8分,共40分)
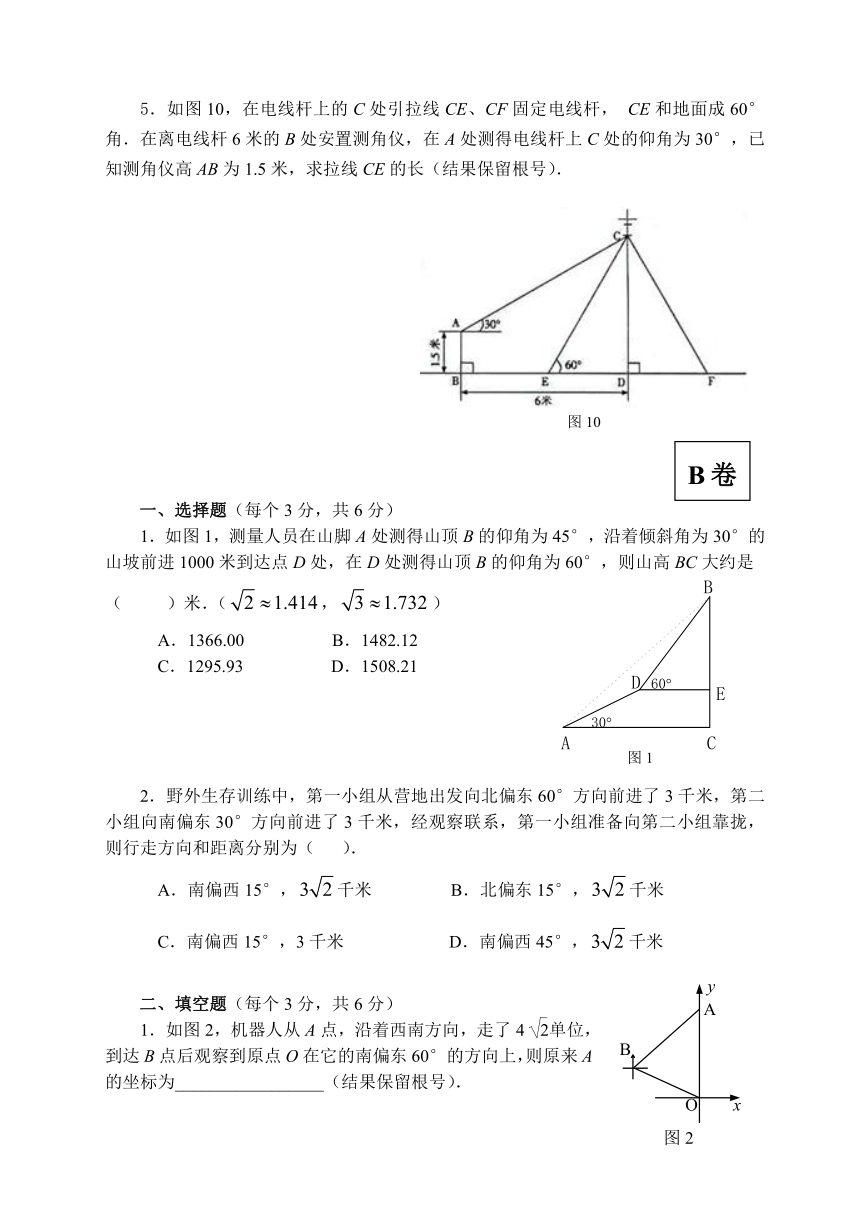
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为、、,根据下列条件解直角三角形
(1),. (2)∠A=30°,.
2.某省将地处A、B两地的两所大学并成一所综合性大学,为了方便两地师生交往,学校准备在相距2km的A、B两地之间修一条笔直的公路.如图7所示,经测量在A地北偏东60°方向、B地北偏西45°方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
3.如图8,AD⊥DC,AB=10,BC=20,∠A=∠C=30°,求AD、CD的长.
4.如图9,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观察点E到地面的距离EF=35cm,求小山BD的高
(精确到0.1海里,≈1.732).
5.如图10,在电线杆上的C处引拉线CE、CF固定电线杆, CE和地面成60°角.在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
一、选择题(每个3分,共6分)
1.如图1,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾斜角为30°的山坡前进1000米到达点D处,在D处测得山顶B的仰角为60°,则山高BC大约是
( )米.(,)
A.1366.00 B.1482.12
C.1295.93 D.1508.21
2.野外生存训练中,第一小组从营地出发向北偏东60°方向前进了3千米,第二小组向南偏东30°方向前进了3千米,经观察联系,第一小组准备向第二小组靠拢,则行走方向和距离分别为( ).
A.南偏西15°,千米 B.北偏东15°,千米
C.南偏西15°,3千米 D.南偏西45°,千米
二、填空题(每个3分,共6分)
1.如图2,机器人从A点,沿着西南方向,走了4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为_________________(结果保留根号).
2.如图3,在Rt△ABC中,∠B=90°,∠A=30°,AC=3,将BC向BA方向折过去,使点C落在BA上的C′点,折痕为BD,则C′D的长是____________.
三、解答题(每题9分,共18分)
1.如图4,小岛A在港口P的南偏西45°方向,距离港口8l海里处.甲船从A出发,
沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以l8海里/时的速度驶离港口.现两船同时出发,
(1)出发后几小时两船与港口P的距离相等
(2)出发后几小时乙船在甲船的正东方向 (结果精确到0.1小时)
(参考数据:)
2.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心.其中心最大风力为12级,每离台风中心20km,风力就会减弱一级,该台风中心正以15km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变,如图5所示.若城市所受风力达到或超过4级,则称为受台风影响.
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
新题推荐(每题10分,共20分)
1.某大型超市为方便顾客购物,准备在一至二楼之间安装电梯,如图1所示,楼顶与地面平行.要使身高2米以下的人在笔直站立的情况下搭乘电梯时,在B处不碰到头部.请你帮该超市设计,电梯与一楼地面的夹角α最大为多少度?
2.在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下方案(如图①所示):
(1)在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=;
(3)量出测倾器的高度AC=.
根据上述测量数据,即可求出旗杆的高度MN.
如果测量工具不变,请仿照上述过程,设计一个测量某小山高度(如图②)的方案:
(1)在图②中,画出你测量小山高度MN的示意图(标上适当字母);
(2)写出你设计的方案.
跟踪训练检测题答案
(测试范围:28.2 解直角三角形)
天津市葛沽第三中学 李玉强 (300352)
A卷:
一、选择题
1.A 2.D 3.C 4.A 5.B 6.D
二、填空题
1. 40° 2. 30° 3. 800 4. 2 5. 30 6. 33.96
三、解答题
1.解:(1)∵,∴∠A=45°,∠B=90°-∠A=45°.
∴.
(2)∠B=90°-∠A=60°,∵,∴,∴,∵,∴,∴.
2.解:如图,过C作CD⊥AB于点D,则CD=BD,不妨设CD=BD,∵∠CAD=30°,∴AD=,由AD+DB=2,有,∴,
∴CD,故计划修筑的公路不会穿过公园.
3.解:如图,过B点分别作BE⊥AD于E,BF⊥CD于F.由AD⊥CD,知四边形BEDF为矩形,则ED=BF,FD=BE.在Rt△AEB中,∠AEB=90°,∠A=30°,
∵AB=10,∴BE=5,AE=.在Rt△CFB中,∠CFB=90°,∠C=30°,BC=20,∴BF=10,CF=.∴AD=AE+ED=,CD=CF+FD=.
4.如图,过点E作EG⊥AD于点G.由已知得∠AEG=60°,∠BEG=45°.
在Rt△BEG中,BG=EG.在Rt△AEG中,由tan∠AEG=,
得AG=EG=BG.又AG=AB+BG=20+BG,
∴BG=20+BG,即BG==10(+1).
∵BD=BG+GD,GD=EF=35,
∴BD=10(+1)+35≈27.32+35=62.32≈62.3(m)
答:小山BD的高约为62.3m.
5.解:过点A作AH⊥CD,垂足为H.由题意可知四边形ABDH为矩形,∠CAH=30o,∴AB=DH=1.5,BD=AH=6.在Rt△ACH中,CH=AHtan∠CAH=2.∴CD=,在Rt△CDE中,∵∠CED=60o,∴CE=(米) .
答:拉线CE的长为米.
B卷
一、选择题:
1.A 2.A
二、填空题:
1.(0,) 2.
三、解答题:
1.(1)设出发后x小时两船与港口P的距离相等.根据题意,得81-9x=18x.解得x=3.∴出发后3小时两船与港口P的距离相等.
(2)设出发后x小时乙船在甲船的正东方.如图,此时甲、乙两船的位置分别在点C、D处,连接CD,过点P作PE⊥CD,垂足为E,则点E在点P的正南方向.
在Rt△CEP中,∠CPE=45°,∴PE=PC·cos45°.
在Rt△PED中,∠EPD=60°,∴PE=PD·cos60°.
∴PC·cos45°=PD·cos60°.∴(81-9x)·cos45°=18x·cos60°.解得x≈3.7
∴出发后约3.7小时乙船在甲船的正东方向.
2.解:过点A作AD⊥BC,垂足为D.∵AB=220,∠B=30o,∴AD=110<160,故该城市会受到这次台风的影响.(2)在BC上取两点E、F,使AE=AF=160.DE=,∴EF=.∵台风中心的速度为15km/h,∴这次台风影响该城市的持续时间为小时.(3)当台风中心位于D处时,A市所受台风的风力最大,其最大风力为6.5级.
C卷
1.解:过点B作BE⊥AD交AD于E,交AC于F.依题意有:BF=2,DE=BC=2.∵CD=4,∴EF=2,由三角形相似可得,AE=.
在Rt△AEF中, ,∴∠α=30°.
答:电梯与一楼地面的夹角最大为30°.
2.解:(1)正确画出示意图(如图).
(2)①在测点A处安置测倾器,测得此时M的仰角;
②在测点A与小山之间的B出安置测倾器(A、B与N在同一条直线上),测得此时山顶M的仰角;
③量出测倾器的高度AC=BD=h,以及测点A、B之间的距离AB=m.根据上述测量数据,即可求出小山的高度MN.
A卷
图2
图1
图4
图3
图5
图6
图7
图8
图9
图10
B卷
图1
x
O
A
y
图2
B
图3
图4
图5
C卷
图1
N
M
②
E
N
A
M
C
①
N
M
α
β
B
A
E
C
D
(测试范围:28.2 解直角三角形)
天津市葛沽第三中学 李玉强 (300352)
一、选择题(每小题5分,共30分)
1.如图1,为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为,则楼房BC的高为( ).
A.30tan米 B.米 C.30sin米 D.米
2.如图2,两建筑物的水平距离为100米,从A点测得D点的俯角为,测得C点的俯角为,则较低建筑物的高为( )米.
A.100 B. C. D.
3.在Rt△ABC中,∠C=90°,cosA=,则tanA=( ).
A. B. C. D.24
4.等腰三角形顶角∠A=120°,高AD=30,则三角形的周长等于( ).
A. B. C. D.
5.如图3,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为( ).
A.m B.m
C.m D.m
6.如图4,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( ).
A. B. C. D.
二、填空题(每题5分,共30分)
1.若地面上的甲看高山上乙的仰角为30°,则乙看到甲的俯角为____________度.
2.等腰三角形的周长为,腰长为1,则底角等于___________.
3.某飞机在离地面1200米的高空测得地面控制点的俯角为60°,此时飞机与该地面控制点之间的距离是 __________ 米.
4.在倾斜角为30°的山坡上种树,要求相邻两棵树间的水平距离为3m,那么,相邻两棵树间的斜坡距离为_____________m.
5.如图5,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是 ________海里/时.
6.如图6,青岛位于北纬36°4′,通过计算可以求得:在冬至日正午时分的太阳入射角为 30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小为_____________ 米,才能保证不挡光?(结果保留四个有效数字)
(提示:sin30°30′=0.5075,tan30°30′=0.5890)
三、解答题 (每题8分,共40分)
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为、、,根据下列条件解直角三角形
(1),. (2)∠A=30°,.
2.某省将地处A、B两地的两所大学并成一所综合性大学,为了方便两地师生交往,学校准备在相距2km的A、B两地之间修一条笔直的公路.如图7所示,经测量在A地北偏东60°方向、B地北偏西45°方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
3.如图8,AD⊥DC,AB=10,BC=20,∠A=∠C=30°,求AD、CD的长.
4.如图9,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观察点E到地面的距离EF=35cm,求小山BD的高
(精确到0.1海里,≈1.732).
5.如图10,在电线杆上的C处引拉线CE、CF固定电线杆, CE和地面成60°角.在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
一、选择题(每个3分,共6分)
1.如图1,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾斜角为30°的山坡前进1000米到达点D处,在D处测得山顶B的仰角为60°,则山高BC大约是
( )米.(,)
A.1366.00 B.1482.12
C.1295.93 D.1508.21
2.野外生存训练中,第一小组从营地出发向北偏东60°方向前进了3千米,第二小组向南偏东30°方向前进了3千米,经观察联系,第一小组准备向第二小组靠拢,则行走方向和距离分别为( ).
A.南偏西15°,千米 B.北偏东15°,千米
C.南偏西15°,3千米 D.南偏西45°,千米
二、填空题(每个3分,共6分)
1.如图2,机器人从A点,沿着西南方向,走了4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为_________________(结果保留根号).
2.如图3,在Rt△ABC中,∠B=90°,∠A=30°,AC=3,将BC向BA方向折过去,使点C落在BA上的C′点,折痕为BD,则C′D的长是____________.
三、解答题(每题9分,共18分)
1.如图4,小岛A在港口P的南偏西45°方向,距离港口8l海里处.甲船从A出发,
沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以l8海里/时的速度驶离港口.现两船同时出发,
(1)出发后几小时两船与港口P的距离相等
(2)出发后几小时乙船在甲船的正东方向 (结果精确到0.1小时)
(参考数据:)
2.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心.其中心最大风力为12级,每离台风中心20km,风力就会减弱一级,该台风中心正以15km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变,如图5所示.若城市所受风力达到或超过4级,则称为受台风影响.
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
新题推荐(每题10分,共20分)
1.某大型超市为方便顾客购物,准备在一至二楼之间安装电梯,如图1所示,楼顶与地面平行.要使身高2米以下的人在笔直站立的情况下搭乘电梯时,在B处不碰到头部.请你帮该超市设计,电梯与一楼地面的夹角α最大为多少度?
2.在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下方案(如图①所示):
(1)在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=;
(3)量出测倾器的高度AC=.
根据上述测量数据,即可求出旗杆的高度MN.
如果测量工具不变,请仿照上述过程,设计一个测量某小山高度(如图②)的方案:
(1)在图②中,画出你测量小山高度MN的示意图(标上适当字母);
(2)写出你设计的方案.
跟踪训练检测题答案
(测试范围:28.2 解直角三角形)
天津市葛沽第三中学 李玉强 (300352)
A卷:
一、选择题
1.A 2.D 3.C 4.A 5.B 6.D
二、填空题
1. 40° 2. 30° 3. 800 4. 2 5. 30 6. 33.96
三、解答题
1.解:(1)∵,∴∠A=45°,∠B=90°-∠A=45°.
∴.
(2)∠B=90°-∠A=60°,∵,∴,∴,∵,∴,∴.
2.解:如图,过C作CD⊥AB于点D,则CD=BD,不妨设CD=BD,∵∠CAD=30°,∴AD=,由AD+DB=2,有,∴,
∴CD,故计划修筑的公路不会穿过公园.
3.解:如图,过B点分别作BE⊥AD于E,BF⊥CD于F.由AD⊥CD,知四边形BEDF为矩形,则ED=BF,FD=BE.在Rt△AEB中,∠AEB=90°,∠A=30°,
∵AB=10,∴BE=5,AE=.在Rt△CFB中,∠CFB=90°,∠C=30°,BC=20,∴BF=10,CF=.∴AD=AE+ED=,CD=CF+FD=.
4.如图,过点E作EG⊥AD于点G.由已知得∠AEG=60°,∠BEG=45°.
在Rt△BEG中,BG=EG.在Rt△AEG中,由tan∠AEG=,
得AG=EG=BG.又AG=AB+BG=20+BG,
∴BG=20+BG,即BG==10(+1).
∵BD=BG+GD,GD=EF=35,
∴BD=10(+1)+35≈27.32+35=62.32≈62.3(m)
答:小山BD的高约为62.3m.
5.解:过点A作AH⊥CD,垂足为H.由题意可知四边形ABDH为矩形,∠CAH=30o,∴AB=DH=1.5,BD=AH=6.在Rt△ACH中,CH=AHtan∠CAH=2.∴CD=,在Rt△CDE中,∵∠CED=60o,∴CE=(米) .
答:拉线CE的长为米.
B卷
一、选择题:
1.A 2.A
二、填空题:
1.(0,) 2.
三、解答题:
1.(1)设出发后x小时两船与港口P的距离相等.根据题意,得81-9x=18x.解得x=3.∴出发后3小时两船与港口P的距离相等.
(2)设出发后x小时乙船在甲船的正东方.如图,此时甲、乙两船的位置分别在点C、D处,连接CD,过点P作PE⊥CD,垂足为E,则点E在点P的正南方向.
在Rt△CEP中,∠CPE=45°,∴PE=PC·cos45°.
在Rt△PED中,∠EPD=60°,∴PE=PD·cos60°.
∴PC·cos45°=PD·cos60°.∴(81-9x)·cos45°=18x·cos60°.解得x≈3.7
∴出发后约3.7小时乙船在甲船的正东方向.
2.解:过点A作AD⊥BC,垂足为D.∵AB=220,∠B=30o,∴AD=110<160,故该城市会受到这次台风的影响.(2)在BC上取两点E、F,使AE=AF=160.DE=,∴EF=.∵台风中心的速度为15km/h,∴这次台风影响该城市的持续时间为小时.(3)当台风中心位于D处时,A市所受台风的风力最大,其最大风力为6.5级.
C卷
1.解:过点B作BE⊥AD交AD于E,交AC于F.依题意有:BF=2,DE=BC=2.∵CD=4,∴EF=2,由三角形相似可得,AE=.
在Rt△AEF中, ,∴∠α=30°.
答:电梯与一楼地面的夹角最大为30°.
2.解:(1)正确画出示意图(如图).
(2)①在测点A处安置测倾器,测得此时M的仰角;
②在测点A与小山之间的B出安置测倾器(A、B与N在同一条直线上),测得此时山顶M的仰角;
③量出测倾器的高度AC=BD=h,以及测点A、B之间的距离AB=m.根据上述测量数据,即可求出小山的高度MN.
A卷
图2
图1
图4
图3
图5
图6
图7
图8
图9
图10
B卷
图1
x
O
A
y
图2
B
图3
图4
图5
C卷
图1
N
M
②
E
N
A
M
C
①
N
M
α
β
B
A
E
C
D
