第28章《锐角三角函数复习》[下学期]
文档属性
| 名称 | 第28章《锐角三角函数复习》[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 33.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-14 00:00:00 | ||
图片预览





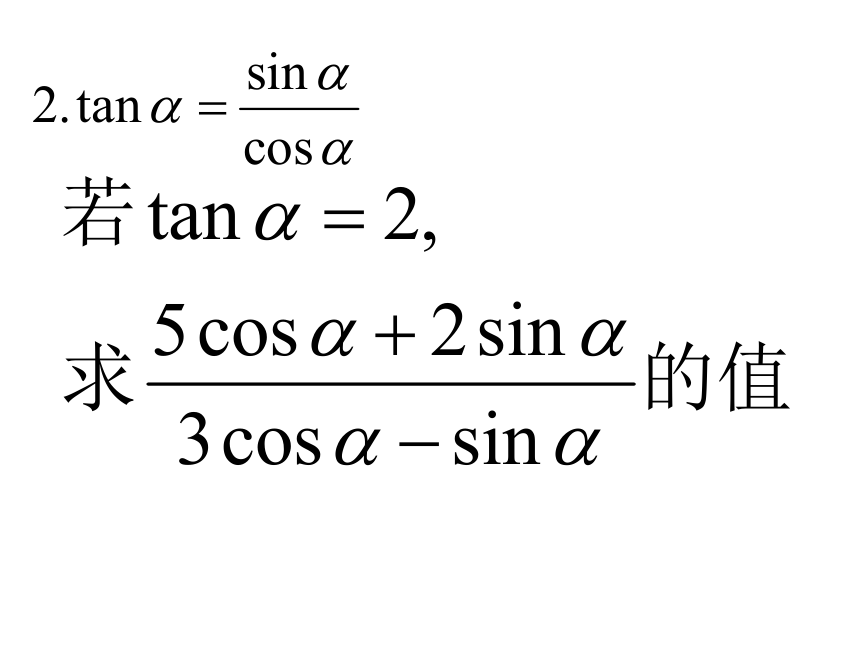
文档简介
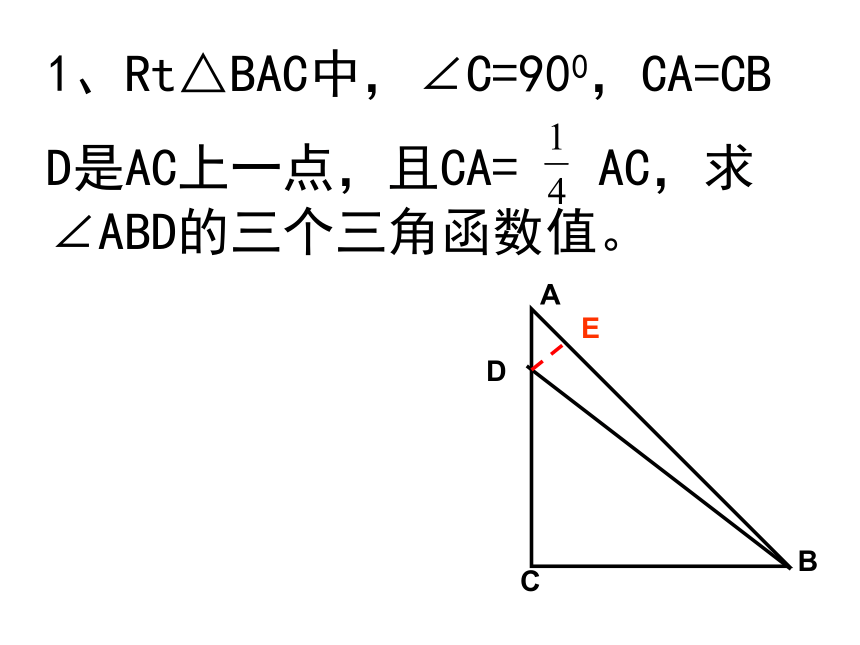
课件17张PPT。第28章《锐角三角函数》复习一、锐角三角函数的两种定义:1、Rt△BAC中,∠C=900,abc则sinA=cosA==cosB=sinBtanA==2、如图,角α的顶点的原点,始边与x正半轴重合,终边上有一点P(x,y)。则sinα=cosα=tanα=α1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且CA= AC,求∠ABD的三个三角函数值。二、特殊角三角函数值1、计算:sin600-tan300+cos4502、在△BAC中,若
则∠C= ,1050三、几个重要结论3、正弦、正切的值随锐角的增大而增大;
余弦的值随锐角的增大而减少。1、锐角A>300,则角A的三个三角函数值的取值范围是什么?则∠A的取值范围是多少?4、解直角三角形:
(1)定义:
(2)几种关系:
(3)几种类型:例1、某中学有一块三角形的花圃△ABC,现可直接测得∠A=300,AC=40,BC=25,求这块花圃的面积。例2、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,5、解直角三角形的应用(1)将实际问题化为数学问题;(画出图形、化为直角三角形问题)(2)选择适当的三角函数解直角三角形;(3)将数学答案写为实际问题答案。6、解题过程中用到的几个概念:(1)仰角、俯角问题;(2)方向角问题;(3)坡角、坡度问题;7、几种基本图形CBDα?βaAαEab?CBDAαβa??EEβαa??αβa??Dh:lα
D是AC上一点,且CA= AC,求∠ABD的三个三角函数值。二、特殊角三角函数值1、计算:sin600-tan300+cos4502、在△BAC中,若
则∠C= ,1050三、几个重要结论3、正弦、正切的值随锐角的增大而增大;
余弦的值随锐角的增大而减少。1、锐角A>300,则角A的三个三角函数值的取值范围是什么?则∠A的取值范围是多少?4、解直角三角形:
(1)定义:
(2)几种关系:
(3)几种类型:例1、某中学有一块三角形的花圃△ABC,现可直接测得∠A=300,AC=40,BC=25,求这块花圃的面积。例2、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,5、解直角三角形的应用(1)将实际问题化为数学问题;(画出图形、化为直角三角形问题)(2)选择适当的三角函数解直角三角形;(3)将数学答案写为实际问题答案。6、解题过程中用到的几个概念:(1)仰角、俯角问题;(2)方向角问题;(3)坡角、坡度问题;7、几种基本图形CBDα?βaAαEab?CBDAαβa??EEβαa??αβa??Dh:lα
