人教版七年级上册4.3.2 角的比较和运算(共16张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.2 角的比较和运算(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 06:29:23 | ||
图片预览


文档简介
(共16张PPT)
4.3.2 角的比较与运算(1)
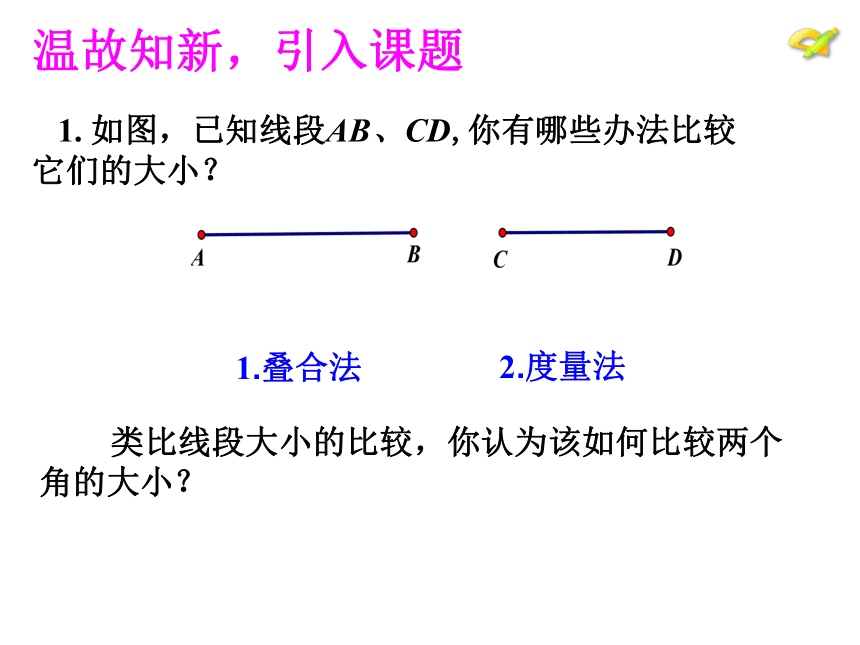
1. 如图,已知线段AB、CD,你有哪些办法比较它们的大小?
温故知新,引入课题
1.叠合法
2.度量法
类比线段大小的比较,你认为该如何比较两个角的大小?
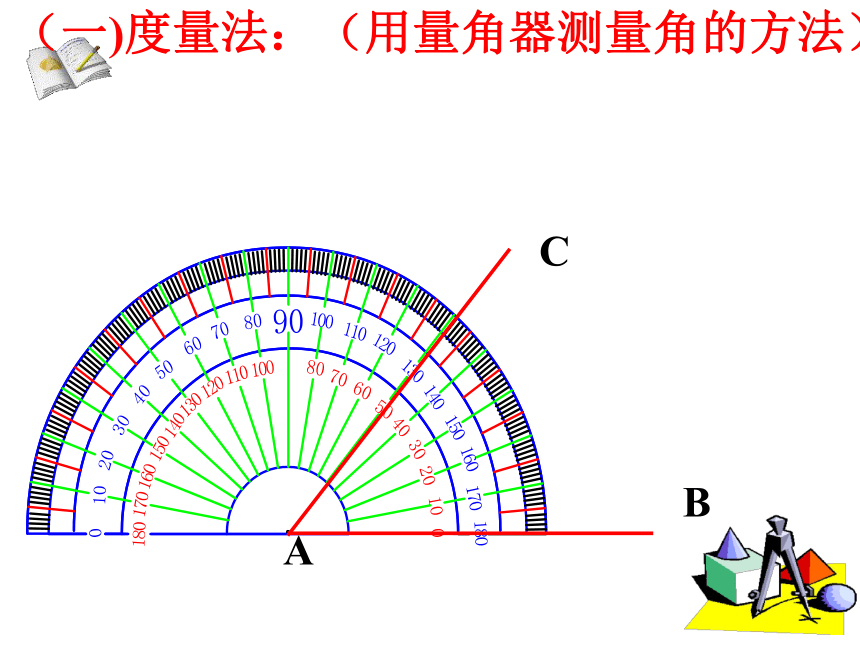
(一)度量法:(用量角器测量角的方法)
A
B
C
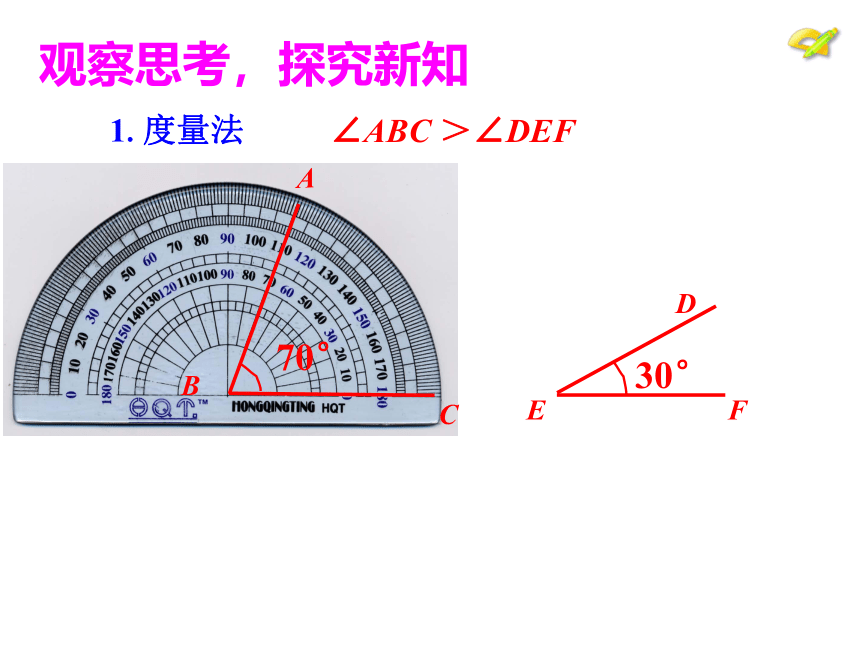
观察思考,探究新知
1.度量法
∠ABC >∠DEF
B
C
A
F
E
D
70°
30°
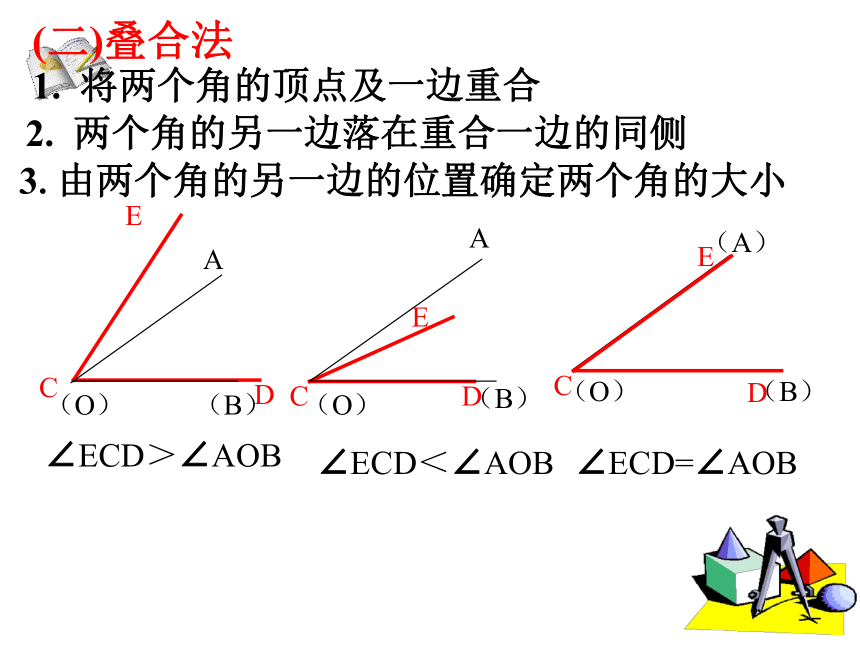
1. 将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
C
D
E
D
C
E
(B)
A
(O)
(O)
A
(B)
(A)
(O)
(B)
C
D
E
∠ECD>∠AOB
∠ECD<∠AOB
∠ECD=∠AOB
(二)叠合法
问题1
图中共有几个角?它们之间有什么关系?
有三个角,关系是:
∠BOC=∠AOC-∠AOB.
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
观察思考,探究新知
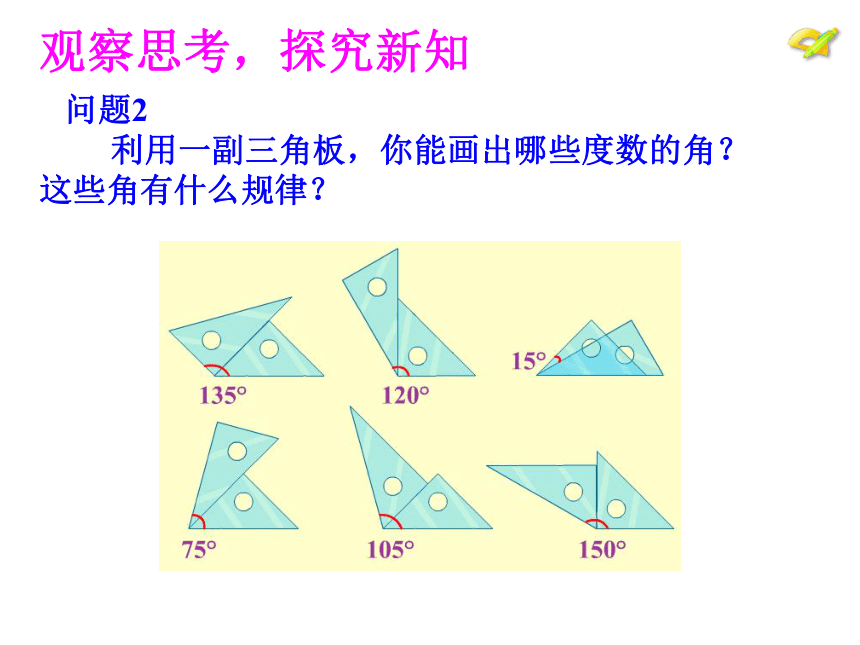
问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
观察思考,探究新知
问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠AOC
∠BOC
类比线段中点的定义,你能给角平分线下定义吗?
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
观察思考,探究新知
α
α
α
两条射线把一个角分成三个相等的角,则这两条射线叫这个角的三等分线
α
α
α
α
角的四等分线
问题4
如何作一个角的平分线?你能想到什么方法?
度量法
折纸法
观察思考,探究新知
例1:如图,O是直线MN上一点,∠NOP= 58°36′42″,求∠MOP的度数.
M
N
P
O
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°- 58°36′42″
=121°23′18″.
答: ∠MOP的度数为121°23′18″.
例2:如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
A
B
C
D
E
O
已知OB是∠AOC的平分线, OD是∠COE的平分 线, 如果 ∠AOE=130度 , 那么∠BOD是多少度
思维拓展
小结与回顾
2.角的和差关系。
3.角的平分线的性质。
1.角的大小比较方法(叠合、度量)。
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小?
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的意义)
∵∠AOB=∠AOC+∠COB=180°
(平角的意义)
A
B
E
C
F
O
4.3.2 角的比较与运算(1)
1. 如图,已知线段AB、CD,你有哪些办法比较它们的大小?
温故知新,引入课题
1.叠合法
2.度量法
类比线段大小的比较,你认为该如何比较两个角的大小?
(一)度量法:(用量角器测量角的方法)
A
B
C
观察思考,探究新知
1.度量法
∠ABC >∠DEF
B
C
A
F
E
D
70°
30°
1. 将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
C
D
E
D
C
E
(B)
A
(O)
(O)
A
(B)
(A)
(O)
(B)
C
D
E
∠ECD>∠AOB
∠ECD<∠AOB
∠ECD=∠AOB
(二)叠合法
问题1
图中共有几个角?它们之间有什么关系?
有三个角,关系是:
∠BOC=∠AOC-∠AOB.
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
观察思考,探究新知
问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
观察思考,探究新知
问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠AOC
∠BOC
类比线段中点的定义,你能给角平分线下定义吗?
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
观察思考,探究新知
α
α
α
两条射线把一个角分成三个相等的角,则这两条射线叫这个角的三等分线
α
α
α
α
角的四等分线
问题4
如何作一个角的平分线?你能想到什么方法?
度量法
折纸法
观察思考,探究新知
例1:如图,O是直线MN上一点,∠NOP= 58°36′42″,求∠MOP的度数.
M
N
P
O
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°- 58°36′42″
=121°23′18″.
答: ∠MOP的度数为121°23′18″.
例2:如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
A
B
C
D
E
O
已知OB是∠AOC的平分线, OD是∠COE的平分 线, 如果 ∠AOE=130度 , 那么∠BOD是多少度
思维拓展
小结与回顾
2.角的和差关系。
3.角的平分线的性质。
1.角的大小比较方法(叠合、度量)。
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小?
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的意义)
∵∠AOB=∠AOC+∠COB=180°
(平角的意义)
A
B
E
C
F
O
