人教版(2019)数学必修第二册6.2平面向量的概念及线性运算课件(共35张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册6.2平面向量的概念及线性运算课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 20:30:20 | ||
图片预览





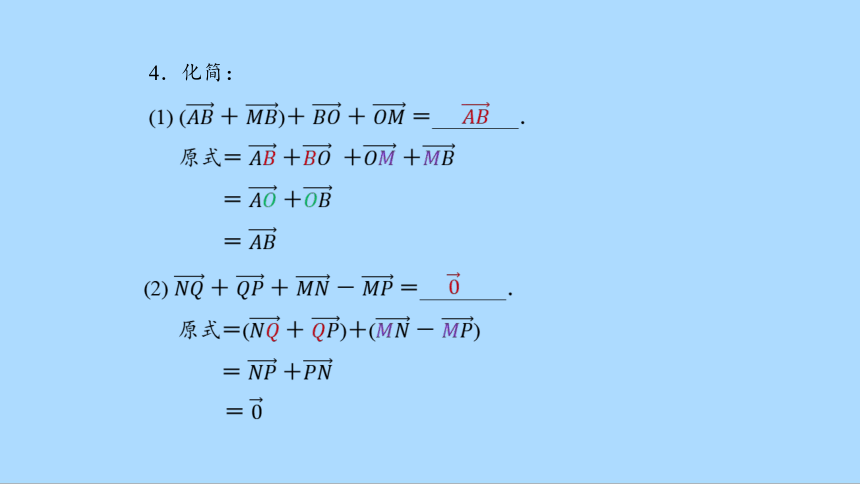




文档简介
(共35张PPT)
6.2平面向量的概念及线性运算
考纲分析
课程标准解读 关联考点 核心素养
1.通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示. 2.通过实例,掌握向量加、减法的运算,并理解其几何意义. 3.掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义. 4.了解向量的线性运算性质及其几何意义. 1.平面向量的有关概念. 2.平面向量的线性运算. 3.共线向量定理的应用. 1.数学抽象.
2.直观想象.
3.数学运算.
课前自测
(4)当两个非零向量a,b共线时,一定有b=λa,反之成立.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.( )
×
(2)若两个向量共线,则其方向必定相同或相反.( )
×
(3)若向量与向量是共线向量,则A,B,C,D四点在一条直线上.( )
×
√
2.(多选)已知m,n是实数,a,b是向量,下列命题正确的是( )
A.m(a-b)=ma-mb
B.(m-n)a=ma-na
C.若ma=mb,则a=b
D.若ma=na,则m=n
×
m=0时不成立
a=0时不成立
×
√
√
AB
3.如图,平行四边形ABCD的对角线交于M,若=a, =b,用a,b表示为( )
A. a+ b B.a-b
C.-a- b D.-a+ b
-a+ b
D
(2) + + - =________.
4.化简:
(1) (+ )+ + =________.
原式= + ++
= +
=
原式=(+ )+(- )
= +
=
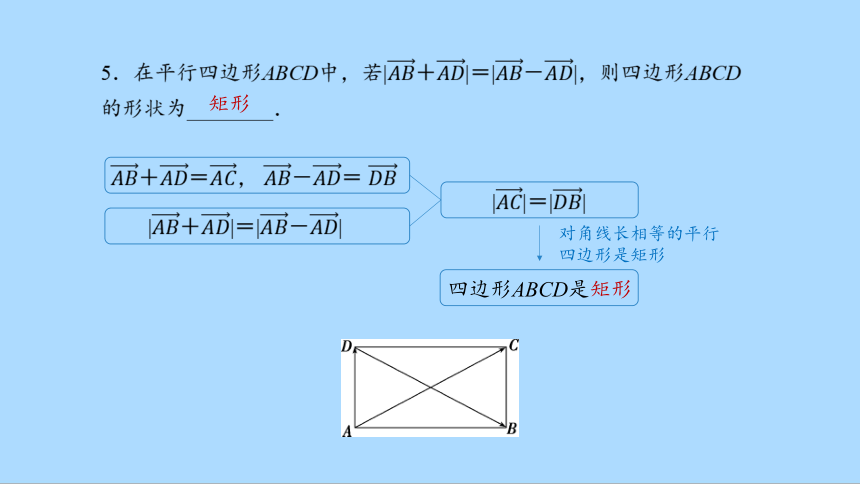
5.在平行四边形ABCD中,若|+|=|-|,则四边形ABCD的形状为________.
+=, -=
|+|=|-|
||=||
四边形ABCD是矩形
对角线长相等的平行四边形是矩形
矩形
考点梳理
1.向量的有关概念
既有大小又有_____的量叫做向量,向量的大小叫做向量的_____.
向量的有关概念
①向量
方向
模
长度为_____的向量,其方向是任意的.
0
③单位向量
长度等于___________的向量.
1个单位
④平行向量
方向相同或____的非零向量,又叫共线向量,规定:0与任一向量共线.
相反
⑤相等向量
长度相等且方向_______的向量.
相同
⑥相反向量
长度相等且方向_______的向量.
相反
②零向量
(1)向量不同于数量,向量不仅有大小,而且还有方向.
注意
(2)任意向量a的模都是非负实数,即|a|≥0.
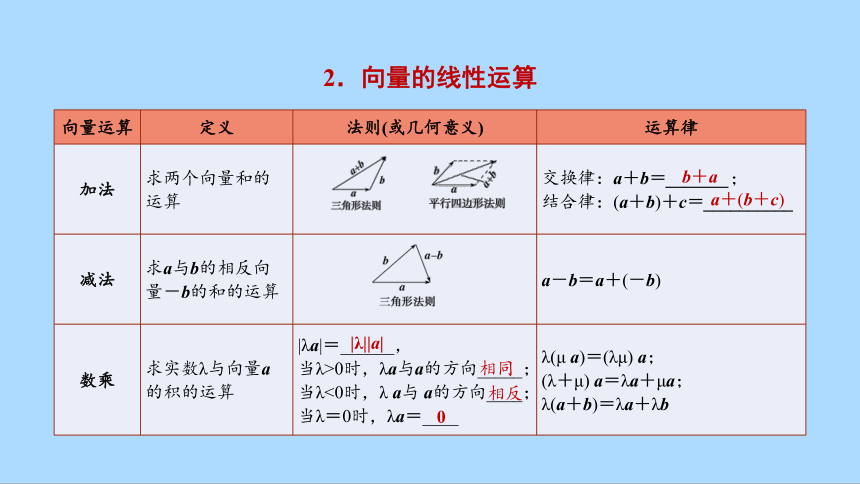
2.向量的线性运算
向量运算 定义 法则(或几何意义) 运算律
加法 求两个向量和的运算 交换律:a+b=_______;
结合律:(a+b)+c=__________
减法 求a与b的相反向量-b的和的运算 a-b=a+(-b)
数乘 求实数λ与向量a的积的运算 |λa|=______, 当λ>0时,λa与a的方向_____; 当λ<0时,λ a与 a的方向____; 当λ=0时,λa=____ λ(μ a)=(λμ) a;
(λ+μ) a=λa+μa;
λ(a+b)=λa+λb
a+(b+c)
b+a
|λ||a|
相同
相反
0
3. 向量共线定理
向量b与非零向量a共线的充要条件是有且只有一个实数λ,使得___________.
b=λa
常用结论
若P为线段AB的中点,O为平面内一点,则= (+).
1.三点共线的等价转化
A,P,B三点共线
=λ(λ≠0)
=(1-t)· +t
(O为平面内异于A,P,B的任一点,t∈R)
=x+y
(O为平面内异于A,P,B的任一点,x∈R,y∈R,x+y=1)
2.向量的中线公式
常见误区
1.若两个向量起点相同,终点相同,则这两个向量相等;但两个相等向量不一定有相同的起点和终点.
3.注意区分向量共线与向量所在的直线平行之间的关系.
2.零向量和单位向量是两个特殊的向量.它们的模确定,但方向不确定.
!
典例剖析
考点
1
平面向量的有关概念
1.设a是非零向量,λ是非零实数,下列结论正确的是( )
A.a与-λa的方向相反 B.|-λa|≥|a|
C.a与λ2a的方向相同 D.|-λa|=|λ|a
C
2.(多选)下列命题中不正确的是( )
A.两个有共同始点且相等的向量,其终点可能不同
B.若非零向量与共线,则A,B,C,D四点共线
C.若非零向量a与b共线,则a=b
D.四边形ABCD是平行四边形,则必有| |=| |
ABC
3.设a,b都是非零向量,下列四个条件中,使成立的充分条件是( )
A.a=-b B.a∥b
C.a=2b D.a∥b且|a|=|b|
C
向量a与向量b方向相同
方法总结
(4) 非零向量与的关系: 是与同方向的单位向量.
(1) 相等向量具有传递性,非零向量的平行也具有传递性.
(2) 共线向量即为平行向量,它们均与起点无关.
(3) 向量可以平移,平移后的向量与原向量是相等向量,解题时,不要把它与函数图象的移动混淆.
平面向量有关概念的四个关注点
[例1] (1) (2020·西安五校联考)如图,AB是圆O的一条直径,C,D是半圆弧的两个三等分点,则=( )
A. - B.2-2
C. - D.2-2
考点
2
平面向量的线性运算
D
C,D是半圆弧的两个三等分点
CD∥AB
且AB=2CD
=2 =2(-)= 2-2
(2) (2020·河南八市联考改编)在等腰梯形ABCD中,=2,点E是线段BC的中点,若=λ+μ,则λ=________,μ=________.
所以λ=,μ=.
A
B
C
D
E
F
取AB的中点F,连接CF,
则由题意可得CF∥AD,且CF=AD.
= +
因为
=+
= +
=+(-)
= +
方法总结
(1) 向量的加减常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连的向量的和用三角形法则.
(2) 找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.
向量线性运算的解题策略
跟踪训练
(2020·吉林梅河口五中4月模拟)在△ABC中,延长BC至点M使得BC=2CM,连接AM,点N为AM上一点且=,若=λ+μ,则λ+μ=( )
A. B. C.- D.-
A
所以λ=-,μ=,则λ+μ= .
= =(+)= +×
= +(-)=-+
A
B
C
M
N
考点
3
平面向量共线定理的应用
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
(2)试确定实数k,使ka+b和a+kb共线.
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
所以A,B,D三点共线.
证明:
因为=a+b, =2a+8b, =3(a-b),
所以= +=2a+8b+3(a-b)=5(a+b)=5,
所以,共线,
又它们有公共点B,
[例2] 设两个非零向量a与b不共线.
(2) 试确定实数k,使ka+b和a+kb共线.
所以k-λ=λk-1=0,所以k2-1=0,
因为ka+b与a+kb共线,
所以存在实数λ,使ka+b=λ(a+kb),
即(k-λ)a=(λk-1)b.
又a,b是两个不共线的非零向量,
所以k=±1.
1.(变条件)若将本例(1)中“=2a+8b”改为“=a+mb”,若A,B,D三点共线,则m=________.
变式探究
所以,解得m=7.
7
+=(a+mb)+3(a-b)=4a+(m-3)b,
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
即=4a+(m-3)b.
若A,B,D三点共线,则存在实数λ,使=λ ,
即4a+(m-3)b=λ(a+b),
故当m=7时,A,B,D三点共线.
变式探究
2.(变结论)若将本例(2)中的“共线”改为“反向共线”,则k=________.
故当k=-1时两向量反向共线.
[例2] 设两个非零向量a与b不共线.
(2) 试确定实数k,使ka+b和a+kb共线.
因为ka+b与a+kb反向共线,
所以存在实数λ,使ka+b=λ(a+kb) (λ<0),
所以所以k=±1.
又λ<0,k=λ,所以k=-1.
-1
方法总结
易错提醒
证明三点共线时,需说明共线的两个向量有公共点.
跟踪训练
即
由=a+mb, =na+b(m,n∈R)共线,
得a+mb=λ(na+b),
1.已知向量a与b不共线,=a+mb, =na+b(m,n∈R),则与共线的条件是( )
A.m+n=0 B.m-n=0
C.mn+1=0 D.mn-1=0
所以mn-1=0.
D
2.已知P是△ABC所在平面内的一点,若=λ+,其中λ∈R,则点P一定在( )
A.△ABC的内部 B.AC边所在直线上
C.AB边所在直线上 D.BC边所在直线上
所以C,P,A三点共线,即点P在直线AC上.
由=λ+得-=λ,=λ.
则,为共线向量,
又,有一个公共点P,
B
随堂检测
1.(多选)已知向量a,b是两个非零向量,在下列四个条件中,一定能使a,b共线的是( )
A.2a-3b=4e且a+2b=-2e
B.存在相异实数λ,μ,使λa-μb=0
C.xa+yb=0(其中实数x,y满足x+y=0)
D.已知梯形ABCD,其中=a, =b
a=e,b=-e,此时能使a,b共线
√
由共线定理知,非零向量a,b是共线向量
√
如果x=y=0,则不能保证a,b共线
×
AB,CD不一定是梯形的上、下底
×
AB
2.若||=||=|-|=2,则|+|=________.
所以|+|=2.
因为||=||=|-| =||=2,
所以△ABC是边长为2的正三角形,
所以|+|为△ABC的边BC上的高的2倍,
2
3.已知e1,e2为平面内两个不共线的向量,=2e1-3e2, =λe1+6e2,若M,N,P三点共线,则λ=________.
可得,解得λ=-4.
因为M,N,P三点共线,
所以存在实数k使得=k,
所以2e1-3e2=k(λe1+6e2),
又e1,e2为平面内两个不共线的向量,
-4
4.已知 ABCD的对角线AC和BD相交于点O,且=a, =b,则=________,=________.(用a,b表示)
=-=--=-a-b.
== - =b-a,
b-a
-a-b
5.在△ABC中,D,E分别为BC,AC边上的中点,G为BE上一点,且GB=2GE,设=a, =b,试用a,b表示,.
= +=+
=+ (+ )
= + (-)
= +
= a+ b.
= (+ )= a+ b;
本课小结
本节知识主要考查平面向量的线性运算(加法、减法、数乘向量)及其几何意义、共线向量定理,有时也会有创新的新定义问题;题型以选择题、填空题为主,属于中低档题目.
6.2平面向量的概念及线性运算
考纲分析
课程标准解读 关联考点 核心素养
1.通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示. 2.通过实例,掌握向量加、减法的运算,并理解其几何意义. 3.掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义. 4.了解向量的线性运算性质及其几何意义. 1.平面向量的有关概念. 2.平面向量的线性运算. 3.共线向量定理的应用. 1.数学抽象.
2.直观想象.
3.数学运算.
课前自测
(4)当两个非零向量a,b共线时,一定有b=λa,反之成立.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.( )
×
(2)若两个向量共线,则其方向必定相同或相反.( )
×
(3)若向量与向量是共线向量,则A,B,C,D四点在一条直线上.( )
×
√
2.(多选)已知m,n是实数,a,b是向量,下列命题正确的是( )
A.m(a-b)=ma-mb
B.(m-n)a=ma-na
C.若ma=mb,则a=b
D.若ma=na,则m=n
×
m=0时不成立
a=0时不成立
×
√
√
AB
3.如图,平行四边形ABCD的对角线交于M,若=a, =b,用a,b表示为( )
A. a+ b B.a-b
C.-a- b D.-a+ b
-a+ b
D
(2) + + - =________.
4.化简:
(1) (+ )+ + =________.
原式= + ++
= +
=
原式=(+ )+(- )
= +
=
5.在平行四边形ABCD中,若|+|=|-|,则四边形ABCD的形状为________.
+=, -=
|+|=|-|
||=||
四边形ABCD是矩形
对角线长相等的平行四边形是矩形
矩形
考点梳理
1.向量的有关概念
既有大小又有_____的量叫做向量,向量的大小叫做向量的_____.
向量的有关概念
①向量
方向
模
长度为_____的向量,其方向是任意的.
0
③单位向量
长度等于___________的向量.
1个单位
④平行向量
方向相同或____的非零向量,又叫共线向量,规定:0与任一向量共线.
相反
⑤相等向量
长度相等且方向_______的向量.
相同
⑥相反向量
长度相等且方向_______的向量.
相反
②零向量
(1)向量不同于数量,向量不仅有大小,而且还有方向.
注意
(2)任意向量a的模都是非负实数,即|a|≥0.
2.向量的线性运算
向量运算 定义 法则(或几何意义) 运算律
加法 求两个向量和的运算 交换律:a+b=_______;
结合律:(a+b)+c=__________
减法 求a与b的相反向量-b的和的运算 a-b=a+(-b)
数乘 求实数λ与向量a的积的运算 |λa|=______, 当λ>0时,λa与a的方向_____; 当λ<0时,λ a与 a的方向____; 当λ=0时,λa=____ λ(μ a)=(λμ) a;
(λ+μ) a=λa+μa;
λ(a+b)=λa+λb
a+(b+c)
b+a
|λ||a|
相同
相反
0
3. 向量共线定理
向量b与非零向量a共线的充要条件是有且只有一个实数λ,使得___________.
b=λa
常用结论
若P为线段AB的中点,O为平面内一点,则= (+).
1.三点共线的等价转化
A,P,B三点共线
=λ(λ≠0)
=(1-t)· +t
(O为平面内异于A,P,B的任一点,t∈R)
=x+y
(O为平面内异于A,P,B的任一点,x∈R,y∈R,x+y=1)
2.向量的中线公式
常见误区
1.若两个向量起点相同,终点相同,则这两个向量相等;但两个相等向量不一定有相同的起点和终点.
3.注意区分向量共线与向量所在的直线平行之间的关系.
2.零向量和单位向量是两个特殊的向量.它们的模确定,但方向不确定.
!
典例剖析
考点
1
平面向量的有关概念
1.设a是非零向量,λ是非零实数,下列结论正确的是( )
A.a与-λa的方向相反 B.|-λa|≥|a|
C.a与λ2a的方向相同 D.|-λa|=|λ|a
C
2.(多选)下列命题中不正确的是( )
A.两个有共同始点且相等的向量,其终点可能不同
B.若非零向量与共线,则A,B,C,D四点共线
C.若非零向量a与b共线,则a=b
D.四边形ABCD是平行四边形,则必有| |=| |
ABC
3.设a,b都是非零向量,下列四个条件中,使成立的充分条件是( )
A.a=-b B.a∥b
C.a=2b D.a∥b且|a|=|b|
C
向量a与向量b方向相同
方法总结
(4) 非零向量与的关系: 是与同方向的单位向量.
(1) 相等向量具有传递性,非零向量的平行也具有传递性.
(2) 共线向量即为平行向量,它们均与起点无关.
(3) 向量可以平移,平移后的向量与原向量是相等向量,解题时,不要把它与函数图象的移动混淆.
平面向量有关概念的四个关注点
[例1] (1) (2020·西安五校联考)如图,AB是圆O的一条直径,C,D是半圆弧的两个三等分点,则=( )
A. - B.2-2
C. - D.2-2
考点
2
平面向量的线性运算
D
C,D是半圆弧的两个三等分点
CD∥AB
且AB=2CD
=2 =2(-)= 2-2
(2) (2020·河南八市联考改编)在等腰梯形ABCD中,=2,点E是线段BC的中点,若=λ+μ,则λ=________,μ=________.
所以λ=,μ=.
A
B
C
D
E
F
取AB的中点F,连接CF,
则由题意可得CF∥AD,且CF=AD.
= +
因为
=+
= +
=+(-)
= +
方法总结
(1) 向量的加减常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连的向量的和用三角形法则.
(2) 找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.
向量线性运算的解题策略
跟踪训练
(2020·吉林梅河口五中4月模拟)在△ABC中,延长BC至点M使得BC=2CM,连接AM,点N为AM上一点且=,若=λ+μ,则λ+μ=( )
A. B. C.- D.-
A
所以λ=-,μ=,则λ+μ= .
= =(+)= +×
= +(-)=-+
A
B
C
M
N
考点
3
平面向量共线定理的应用
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
(2)试确定实数k,使ka+b和a+kb共线.
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
所以A,B,D三点共线.
证明:
因为=a+b, =2a+8b, =3(a-b),
所以= +=2a+8b+3(a-b)=5(a+b)=5,
所以,共线,
又它们有公共点B,
[例2] 设两个非零向量a与b不共线.
(2) 试确定实数k,使ka+b和a+kb共线.
所以k-λ=λk-1=0,所以k2-1=0,
因为ka+b与a+kb共线,
所以存在实数λ,使ka+b=λ(a+kb),
即(k-λ)a=(λk-1)b.
又a,b是两个不共线的非零向量,
所以k=±1.
1.(变条件)若将本例(1)中“=2a+8b”改为“=a+mb”,若A,B,D三点共线,则m=________.
变式探究
所以,解得m=7.
7
+=(a+mb)+3(a-b)=4a+(m-3)b,
[例2] 设两个非零向量a与b不共线.
(1)若=a+b, =2a+8b, =3(a-b),求证:A,B,D三点共线;
即=4a+(m-3)b.
若A,B,D三点共线,则存在实数λ,使=λ ,
即4a+(m-3)b=λ(a+b),
故当m=7时,A,B,D三点共线.
变式探究
2.(变结论)若将本例(2)中的“共线”改为“反向共线”,则k=________.
故当k=-1时两向量反向共线.
[例2] 设两个非零向量a与b不共线.
(2) 试确定实数k,使ka+b和a+kb共线.
因为ka+b与a+kb反向共线,
所以存在实数λ,使ka+b=λ(a+kb) (λ<0),
所以所以k=±1.
又λ<0,k=λ,所以k=-1.
-1
方法总结
易错提醒
证明三点共线时,需说明共线的两个向量有公共点.
跟踪训练
即
由=a+mb, =na+b(m,n∈R)共线,
得a+mb=λ(na+b),
1.已知向量a与b不共线,=a+mb, =na+b(m,n∈R),则与共线的条件是( )
A.m+n=0 B.m-n=0
C.mn+1=0 D.mn-1=0
所以mn-1=0.
D
2.已知P是△ABC所在平面内的一点,若=λ+,其中λ∈R,则点P一定在( )
A.△ABC的内部 B.AC边所在直线上
C.AB边所在直线上 D.BC边所在直线上
所以C,P,A三点共线,即点P在直线AC上.
由=λ+得-=λ,=λ.
则,为共线向量,
又,有一个公共点P,
B
随堂检测
1.(多选)已知向量a,b是两个非零向量,在下列四个条件中,一定能使a,b共线的是( )
A.2a-3b=4e且a+2b=-2e
B.存在相异实数λ,μ,使λa-μb=0
C.xa+yb=0(其中实数x,y满足x+y=0)
D.已知梯形ABCD,其中=a, =b
a=e,b=-e,此时能使a,b共线
√
由共线定理知,非零向量a,b是共线向量
√
如果x=y=0,则不能保证a,b共线
×
AB,CD不一定是梯形的上、下底
×
AB
2.若||=||=|-|=2,则|+|=________.
所以|+|=2.
因为||=||=|-| =||=2,
所以△ABC是边长为2的正三角形,
所以|+|为△ABC的边BC上的高的2倍,
2
3.已知e1,e2为平面内两个不共线的向量,=2e1-3e2, =λe1+6e2,若M,N,P三点共线,则λ=________.
可得,解得λ=-4.
因为M,N,P三点共线,
所以存在实数k使得=k,
所以2e1-3e2=k(λe1+6e2),
又e1,e2为平面内两个不共线的向量,
-4
4.已知 ABCD的对角线AC和BD相交于点O,且=a, =b,则=________,=________.(用a,b表示)
=-=--=-a-b.
== - =b-a,
b-a
-a-b
5.在△ABC中,D,E分别为BC,AC边上的中点,G为BE上一点,且GB=2GE,设=a, =b,试用a,b表示,.
= +=+
=+ (+ )
= + (-)
= +
= a+ b.
= (+ )= a+ b;
本课小结
本节知识主要考查平面向量的线性运算(加法、减法、数乘向量)及其几何意义、共线向量定理,有时也会有创新的新定义问题;题型以选择题、填空题为主,属于中低档题目.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
