人教版(2019)数学必修第二册8.6.1直线与直线垂直课件(共31张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8.6.1直线与直线垂直课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 649.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 20:48:48 | ||
图片预览










文档简介
(共31张PPT)
8.6.1 直线与直线垂直
高一
必修二
本节目标
1.了解空间中两条直线的三种位置关系,理解异面直线的定义,会用平面衬托来画异面直线.
2.会用异面直线所成的角的定义找出或作出异面直线所成的角,会在直角三角形中求简单异面直线所成的角.
预习课本P146~148,思考并完成以下问题
课前预习
1.空间两直线有哪几种位置关系?什么是异面直线?
2.什么是异面直线所成的角?
3.异面直线所成角的范围如何?什么是异面直线垂直?
课前小测
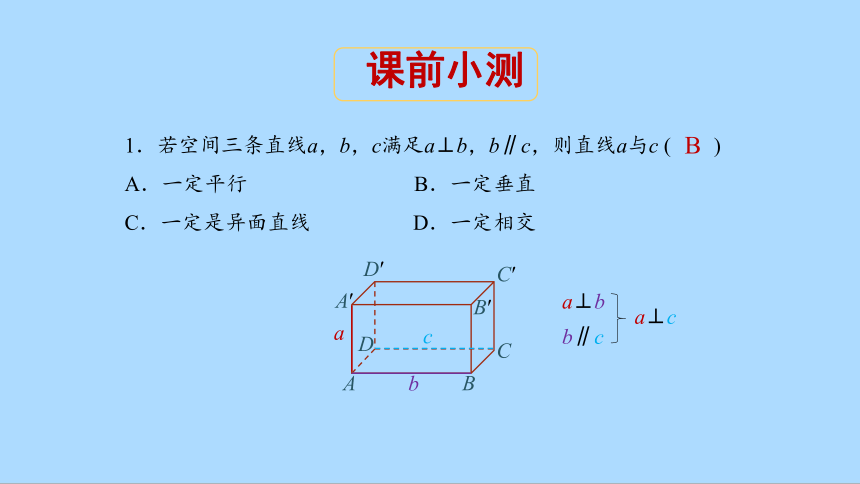
1.若空间三条直线a,b,c满足a⊥b,b∥c,则直线a与c ( )
A.一定平行 B.一定垂直
C.一定是异面直线 D.一定相交
A
B
C
D
A′
B′
C′
D′
a
b
c
B
a⊥b
b∥c
a⊥c
2.若∠AOB=120°,直线a∥OA,a与OB为异面直线,则a和OB所成的角的大小为__________.
因为a∥OA,根据等角定理,
又因为异面直线所成的角为锐角或直角,
所以a与OB所成的角为60°.
60°
3.已知正方体ABCD -EFGH,则AH与FG所成的角是________.
连接BG,则BG∥AH,
所以∠BGF为异面直线AH与FG所成的角.
因为四边形BCGF为正方形,
所以∠BGF=45°.
45°
新课导入
复习回顾
空间两直线的位置关系
(1)从公共点的个数来看可分为:
①有且只有一个公共点——两直线相交
α
l1
l2
记作:l1 ∩ l2=A
②没有公共点
两直线平行
记作: l1 ∥ l2
两直线为异面直线
α
l1
l2
(2)从平面的性质来讲,可分为:
①在同一平面内
两直线相交
两直线平行
②不同在任何一个平面内——两直线为异面直线
观察
如图,在正方体ABCD -A′B′C′D′中,直线A′C′与直线AB,直线A′D′与直线AB都是异面直线,直线A′C′与A′D′相对于直线AB的位置相同吗?如果不同,如何表示这种差异呢?
A
B
C
D
A′
B′
C′
D′
新知探究
1.异面直线所成的角
在平面内,两条直线相交成四个角,其中不大于90°的角称为它们的夹角,用以刻画两直线的错开程度,如图.
O
思考:异面直线有没有夹角呢?若有,如何找出这个夹角?
1.异面直线所成的角
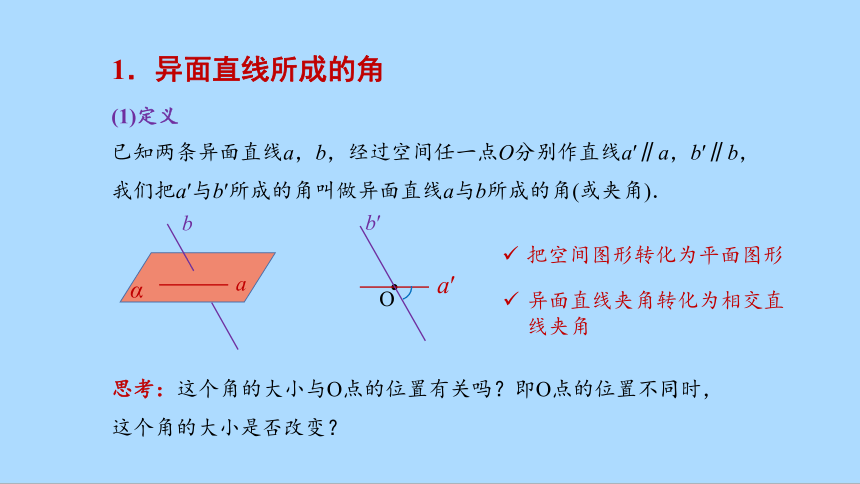
已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
(1)定义
α
a
b
O
a′
b′
把空间图形转化为平面图形
异面直线夹角转化为相交直线夹角
思考:这个角的大小与O点的位置有关吗?即O点的位置不同时,这个角的大小是否改变?
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
(2)异面直线所成的角θ的取值范围
注意:空间两条直线所成角α的取值范围是0°≤ θ≤90°
0°<θ≤90°
(1)任意性与无关性:在定义中,空间一点O是任取的,根据等角定理,可以断定异面直线所成的角与a′,b′所成的锐角(或直角)相等,而与点O的位置无关.
(2)转化求角:异面直线所成的角是刻画两条异面直线相对位置的一个重要的量,通过转化为相交直线所成的角,将空间角转化为平面角来计算.
(3)两条直线垂直是指相交垂直或异面垂直.
2.理解异面直线所成角的注意点
题型突破
典例深度剖析 重点多维探究
题型一 求异面直线所成的角
[例1] 如图,三棱锥A- BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
过点F作MF∥BD,交BC于点M,连接ME,
则CM∶MB=CF∶FD=m,
又因为AE∶EB=CF∶FD=m,
所以CM∶MB=AE∶EB,
所以EM∥AC,
所以α=∠MEF,β=∠MFE,
AC与BD所成的角为∠EMF,
因为AC⊥BD,∴∠EMF=90°,
所以α+β=90°.
[例1] 如图,三棱锥A- BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
总结提升
(1)找出(或作出)适合题设的角——用平移法,遇题设中有中点,常考虑中位线;若异面直线依附于某几何体,且直线对异面直线平移有困难时,可利用该几何体的特殊点,使异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.
(3)结论——设由(2)所求得的角的大小为θ. 若0°<θ≤90°,则θ为所求;若90°<θ<180°,则180°-θ为所求.
求异面直线所成的角的一般步骤
跟踪训练
1.[变条件,变结论]将本例变为:如图所示,点A是平面BCD外一点,AD=BC=2,E,F分别是AB,CD的中点,且EF=,求异面直线AD和BC所成的角.
如图,设G是AC的中点,连接EG,FG.
因为E,F分别是AB,CD的中点,
故EG∥BC且EG= BC=1,
FG∥AD,且FG= AD=1.
即∠EGF为所求,
又EF=,由勾股定理逆定理可得∠EGF=90°.
G
2.正方体ABCD -A′B′C′D′中,E,F分别为平面A′B′C′D′与AA′D′D的中心,则EF与CD所成角的度数是________.
因为∠B′AB=45°
连接B′D′,则E为B′D′的中点,连接AB′,则EF∥AB′,
又CD∥AB
所以∠B′AB为异面直线EF与CD所成角
所以EF与CD所成角的度数是45°
45°
题型二 证明直线与直线垂直问题
[例2] 如图,已知在长方体ABCD -A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点.
求证:CD1⊥EF.
[证明] 取CD1的中点G,连接EG,DG.
因为E是BD1的中点,所以EG∥BC,EG= BC.
因为F是AD的中点,且AD∥BC,AD=BC,
所以DF∥BC,DF= BC.
所以EG∥DF,EG=DF.
所以四边形EFDG是平行四边形,所以EF∥DG,
又A1A=AB,所以四边形ABB1A1、四边形CDD1C1都是正方形,
且G为CD1的中点,
所以DG⊥CD1,所以CD1⊥EF.
[例2] 如图,已知在长方体ABCD -A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点.
求证:CD1⊥EF.
总结提升
(1)对于共面垂直的两条直线的证明,可根据勾股定理证明.
证明两条直线垂直的策略
(2)对于异面垂直的两条直线的证明,可转化为求两条异面直线所成的角为90°来证明.
证明:如图,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°,即DB1⊥EF.
跟踪训练
2. 在正方体AC1中,E,F分别是A1B1,B1C1的中点,求证:DB1⊥EF.
随堂检测
1.如图,已知正方体ABCD- A′B′C′D′.
(3)哪些棱所在的直线与直线AA′垂直?
直线AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′分别与直线AA′垂直.
(1)哪些棱所在直线与直线BA′是异面直线?
(2)直线BA′和CC′的夹角是多少?
棱AD、DC、CC′、DD′、D′C′、B′C′所在直线分别与直线BA′是异面直线
由BB′∥CC′可知,∠B′BA′为异面直线BA′与CC′的夹角,∠B′BA′=45°,所以直线BA′和CC′的夹角为45°.
2.如图,在正方体ABCD -A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60°
C.90° D.120°
取A1B1中点I,连接IG、IH,则EF IG.
易知IG,IH,HG相等,
则△HGI为等边三角形,
则IG与GH所成的角为60°,
即EF与GH所成的角为60°.
I
B
3.如图,正方体ABCD- A1B1C1D1中,AC与BC1所成角的大小是_________.
连接AD1,则AD1∥BC1.
∴∠CAD1(或其补角)就是AC与BC1所成的角,连接CD1,
在正方体ABCD-A1B1C1D1中,AC=AD1=CD1,
∴∠CAD1=60°,
即AC与BC1所成的角为60°.
60°
4.如图,在四棱锥P -ABCD中,PA⊥AB,底面ABCD是平行四边形,则PA与CD所成的角是_______.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠PAB是PA与CD所成的角.
又∵PA⊥AB,
∴∠PAB=90°.
90°
本课小结
1.在研究异面直线所成角的大小时,通常把两条异面直线所成的角转化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成角的范围为(0°,90°],解题时经常结合这一点去求异面直线所成角的大小.
2.作异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).
通过本节课,你学会了什么?
8.6.1 直线与直线垂直
高一
必修二
本节目标
1.了解空间中两条直线的三种位置关系,理解异面直线的定义,会用平面衬托来画异面直线.
2.会用异面直线所成的角的定义找出或作出异面直线所成的角,会在直角三角形中求简单异面直线所成的角.
预习课本P146~148,思考并完成以下问题
课前预习
1.空间两直线有哪几种位置关系?什么是异面直线?
2.什么是异面直线所成的角?
3.异面直线所成角的范围如何?什么是异面直线垂直?
课前小测
1.若空间三条直线a,b,c满足a⊥b,b∥c,则直线a与c ( )
A.一定平行 B.一定垂直
C.一定是异面直线 D.一定相交
A
B
C
D
A′
B′
C′
D′
a
b
c
B
a⊥b
b∥c
a⊥c
2.若∠AOB=120°,直线a∥OA,a与OB为异面直线,则a和OB所成的角的大小为__________.
因为a∥OA,根据等角定理,
又因为异面直线所成的角为锐角或直角,
所以a与OB所成的角为60°.
60°
3.已知正方体ABCD -EFGH,则AH与FG所成的角是________.
连接BG,则BG∥AH,
所以∠BGF为异面直线AH与FG所成的角.
因为四边形BCGF为正方形,
所以∠BGF=45°.
45°
新课导入
复习回顾
空间两直线的位置关系
(1)从公共点的个数来看可分为:
①有且只有一个公共点——两直线相交
α
l1
l2
记作:l1 ∩ l2=A
②没有公共点
两直线平行
记作: l1 ∥ l2
两直线为异面直线
α
l1
l2
(2)从平面的性质来讲,可分为:
①在同一平面内
两直线相交
两直线平行
②不同在任何一个平面内——两直线为异面直线
观察
如图,在正方体ABCD -A′B′C′D′中,直线A′C′与直线AB,直线A′D′与直线AB都是异面直线,直线A′C′与A′D′相对于直线AB的位置相同吗?如果不同,如何表示这种差异呢?
A
B
C
D
A′
B′
C′
D′
新知探究
1.异面直线所成的角
在平面内,两条直线相交成四个角,其中不大于90°的角称为它们的夹角,用以刻画两直线的错开程度,如图.
O
思考:异面直线有没有夹角呢?若有,如何找出这个夹角?
1.异面直线所成的角
已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
(1)定义
α
a
b
O
a′
b′
把空间图形转化为平面图形
异面直线夹角转化为相交直线夹角
思考:这个角的大小与O点的位置有关吗?即O点的位置不同时,这个角的大小是否改变?
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
(2)异面直线所成的角θ的取值范围
注意:空间两条直线所成角α的取值范围是0°≤ θ≤90°
0°<θ≤90°
(1)任意性与无关性:在定义中,空间一点O是任取的,根据等角定理,可以断定异面直线所成的角与a′,b′所成的锐角(或直角)相等,而与点O的位置无关.
(2)转化求角:异面直线所成的角是刻画两条异面直线相对位置的一个重要的量,通过转化为相交直线所成的角,将空间角转化为平面角来计算.
(3)两条直线垂直是指相交垂直或异面垂直.
2.理解异面直线所成角的注意点
题型突破
典例深度剖析 重点多维探究
题型一 求异面直线所成的角
[例1] 如图,三棱锥A- BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
过点F作MF∥BD,交BC于点M,连接ME,
则CM∶MB=CF∶FD=m,
又因为AE∶EB=CF∶FD=m,
所以CM∶MB=AE∶EB,
所以EM∥AC,
所以α=∠MEF,β=∠MFE,
AC与BD所成的角为∠EMF,
因为AC⊥BD,∴∠EMF=90°,
所以α+β=90°.
[例1] 如图,三棱锥A- BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
总结提升
(1)找出(或作出)适合题设的角——用平移法,遇题设中有中点,常考虑中位线;若异面直线依附于某几何体,且直线对异面直线平移有困难时,可利用该几何体的特殊点,使异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.
(3)结论——设由(2)所求得的角的大小为θ. 若0°<θ≤90°,则θ为所求;若90°<θ<180°,则180°-θ为所求.
求异面直线所成的角的一般步骤
跟踪训练
1.[变条件,变结论]将本例变为:如图所示,点A是平面BCD外一点,AD=BC=2,E,F分别是AB,CD的中点,且EF=,求异面直线AD和BC所成的角.
如图,设G是AC的中点,连接EG,FG.
因为E,F分别是AB,CD的中点,
故EG∥BC且EG= BC=1,
FG∥AD,且FG= AD=1.
即∠EGF为所求,
又EF=,由勾股定理逆定理可得∠EGF=90°.
G
2.正方体ABCD -A′B′C′D′中,E,F分别为平面A′B′C′D′与AA′D′D的中心,则EF与CD所成角的度数是________.
因为∠B′AB=45°
连接B′D′,则E为B′D′的中点,连接AB′,则EF∥AB′,
又CD∥AB
所以∠B′AB为异面直线EF与CD所成角
所以EF与CD所成角的度数是45°
45°
题型二 证明直线与直线垂直问题
[例2] 如图,已知在长方体ABCD -A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点.
求证:CD1⊥EF.
[证明] 取CD1的中点G,连接EG,DG.
因为E是BD1的中点,所以EG∥BC,EG= BC.
因为F是AD的中点,且AD∥BC,AD=BC,
所以DF∥BC,DF= BC.
所以EG∥DF,EG=DF.
所以四边形EFDG是平行四边形,所以EF∥DG,
又A1A=AB,所以四边形ABB1A1、四边形CDD1C1都是正方形,
且G为CD1的中点,
所以DG⊥CD1,所以CD1⊥EF.
[例2] 如图,已知在长方体ABCD -A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点.
求证:CD1⊥EF.
总结提升
(1)对于共面垂直的两条直线的证明,可根据勾股定理证明.
证明两条直线垂直的策略
(2)对于异面垂直的两条直线的证明,可转化为求两条异面直线所成的角为90°来证明.
证明:如图,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°,即DB1⊥EF.
跟踪训练
2. 在正方体AC1中,E,F分别是A1B1,B1C1的中点,求证:DB1⊥EF.
随堂检测
1.如图,已知正方体ABCD- A′B′C′D′.
(3)哪些棱所在的直线与直线AA′垂直?
直线AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′分别与直线AA′垂直.
(1)哪些棱所在直线与直线BA′是异面直线?
(2)直线BA′和CC′的夹角是多少?
棱AD、DC、CC′、DD′、D′C′、B′C′所在直线分别与直线BA′是异面直线
由BB′∥CC′可知,∠B′BA′为异面直线BA′与CC′的夹角,∠B′BA′=45°,所以直线BA′和CC′的夹角为45°.
2.如图,在正方体ABCD -A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60°
C.90° D.120°
取A1B1中点I,连接IG、IH,则EF IG.
易知IG,IH,HG相等,
则△HGI为等边三角形,
则IG与GH所成的角为60°,
即EF与GH所成的角为60°.
I
B
3.如图,正方体ABCD- A1B1C1D1中,AC与BC1所成角的大小是_________.
连接AD1,则AD1∥BC1.
∴∠CAD1(或其补角)就是AC与BC1所成的角,连接CD1,
在正方体ABCD-A1B1C1D1中,AC=AD1=CD1,
∴∠CAD1=60°,
即AC与BC1所成的角为60°.
60°
4.如图,在四棱锥P -ABCD中,PA⊥AB,底面ABCD是平行四边形,则PA与CD所成的角是_______.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠PAB是PA与CD所成的角.
又∵PA⊥AB,
∴∠PAB=90°.
90°
本课小结
1.在研究异面直线所成角的大小时,通常把两条异面直线所成的角转化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成角的范围为(0°,90°],解题时经常结合这一点去求异面直线所成角的大小.
2.作异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
