人教版(2019)数学必修第二册8.6.3平面与平面垂直(2)课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8.6.3平面与平面垂直(2)课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 659.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 20:50:24 | ||
图片预览









文档简介
(共34张PPT)
8.6.3 平面与平面垂直(2)
高一
必修二
本节目标
1. 掌握面面垂直的性质定理,能应用定理证明垂直关系.
2. 理解线线垂直、线面垂直、面面垂直的转化关系
预习课本P159~161,思考并完成以下问题
1.平面与平面垂直的性质定理是什么?
2.两个平面互相垂直可以推出哪些结论?
课前预习
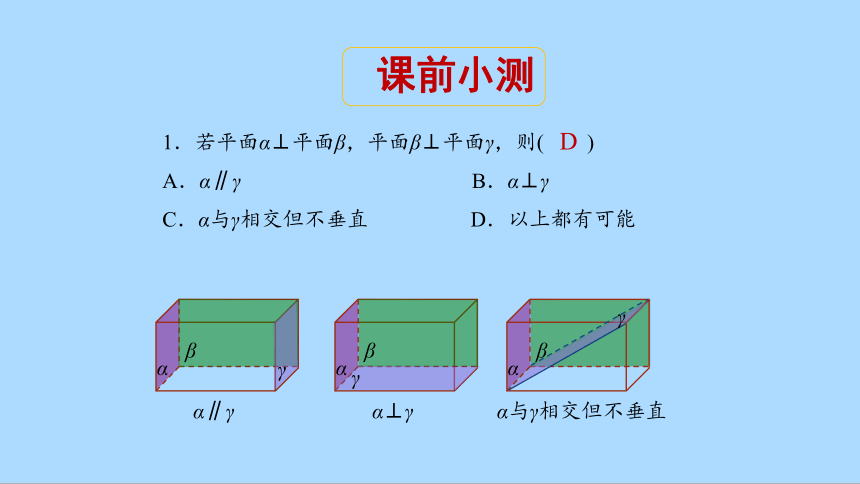
1.若平面α⊥平面β,平面β⊥平面γ,则( )
A.α∥γ B.α⊥γ
C.α与γ相交但不垂直 D.以上都有可能
α
β
γ
α∥γ
α
β
α⊥γ
γ
α
β
α与γ相交但不垂直
γ
D
课前小测
2.平面α⊥平面β,α∩β=l,m α,m⊥l,则( )
A.m∥β B.m β
C.m⊥β D.m与β相交但不一定垂直
α⊥β
α∩β=l
m α
m⊥l
m⊥β
C
3.若两个平面互相垂直,在第一个平面内的一条直线a垂直于第二个平面内的一条直线b,那么( )
A.直线a垂直于第二个平面
B.直线b垂直于第一个平面
C.直线a不一定垂直于第二个平面
D.过a的平面必垂直于过b的平面
直线a与直线b均不一定为两面的交线.
C
4.平面α⊥平面β,α∩β=l,n β,n⊥l,直线m⊥α,则直线m与n的位置关系是__________.
平行
α⊥β
α∩β=l
n β
n⊥l
n⊥α
m⊥α
m∥n
新课导入
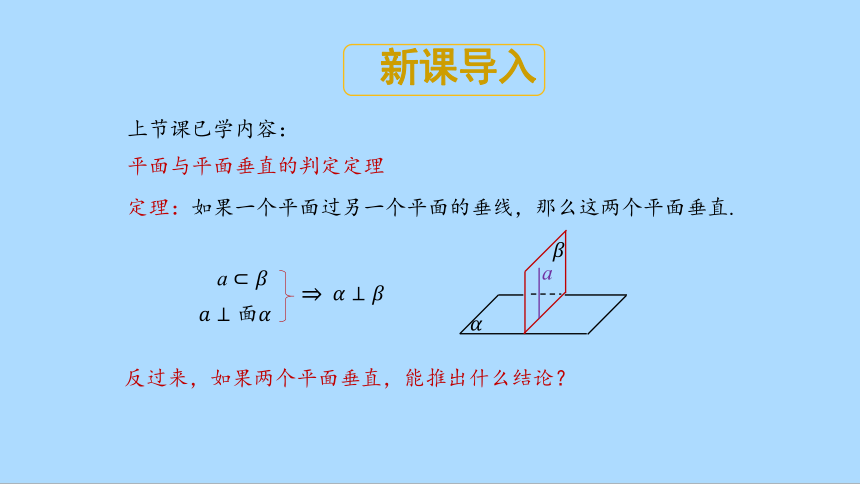
上节课已学内容:
平面与平面垂直的判定定理
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
a
a
反过来,如果两个平面垂直,能推出什么结论?
新知探究
探究
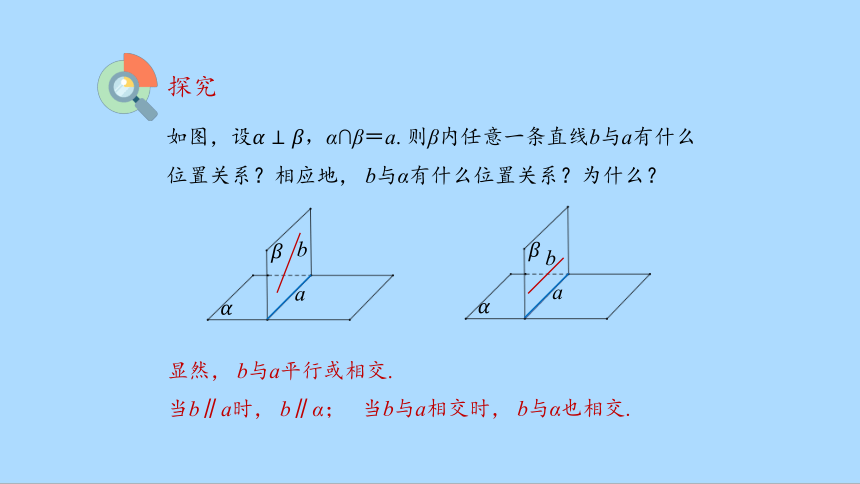
如图,设,α∩β=a. 则β内任意一条直线b与a有什么位置关系?相应地, b与α有什么位置关系?为什么?
a
b
显然, b与a平行或相交.
当b∥a时, b∥α;
当b与a相交时, b与α也相交.
a
b
特别的,当ba时,如图,设b与a的交点为A,过点A在内作直线ca,则直线b,c所成的角就是二面角- a- β的平面角.
由知, b c.
又因为ba, a 和c是内的两条相交直线,所以b.
a
b
A
c
由此可以得到平面与平面垂直的性质定理.
1.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的______,那么这条直线与另一个平面垂直
符号语言 a⊥β
图形语言
作用 ①面面垂直 线面垂直
②作面的垂线
交线
2.对面面垂直的性质定理的理解
(1)定理成立的条件有三个
①两个平面互相垂直;
②直线在其中一个平面内;
③直线与两平面的交线垂直.
(2)定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
(3)已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线垂直.
探究
设平面,点P在平面内,过点P作平面β的垂线a,直线a与平面具有什么位置关系?
P
a
b
P
b
c
c
a
如图,设,过点P在平面内作直线b c,根据平面与平面垂直的性质定理, b .因为过一点有且只有一条直线与平面垂直,所以直线a与直线b重合,因此a .
平面与平面垂直的性质定理2
两平面垂直,过一个平面内一点,垂直于第二个平面的直线在第一个平面内.
a
P
a
c
题型突破
典例深度剖析 重点多维探究
题型一 利用面面垂直的性质定理证明垂直
[例1] 如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于平面ABCD.若G为AD边的中点.
求证:平面PBG⊥平面PAD.
[证明] ∵四边形ABCD是菱形,∠DAB=60°,
∴△ABD是正三角形.
∵G为AD边的中点,
∴BG⊥AD.
∵平面PAD⊥平面ABCD,BG 平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
∵BG 平面PBG,
∴平面PBG⊥平面PAD.
[例1] 如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于平面ABCD.若G为AD边的中点.
求证:平面PBG⊥平面PAD.
总结提升
应用面面垂直性质定理证明相关问题时,一般需要作辅助线——过其中一个平面内一点作交线的垂线,使之转化为线面垂直,然后,进一步转化为线线垂直.
应用面面垂直性质定理要注意的问题
跟踪训练
1. 如图所示,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面PBC.
求证:BC⊥AC.
证明:如图,在平面PAC内作AD⊥PC交PC于点D,
∵平面PAC⊥平面PBC,AD 平面PAC,
且AD⊥PC,平面PAC∩平面PBC=PC,
∴AD⊥平面PBC,又∵BC 平面PBC,∴AD⊥BC.
∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC,
∵AD∩PA=A,∴BC⊥平面PAC,
∵AC 平面PAC,∴BC⊥AC.
D
题型二 线线、线面、面面垂直的综合
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点.
求证:(1)EN∥平面PDC;
(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADMN.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(1)EN∥平面PDC;
[证明] ∵AD∥BC,BC 平面PBC,AD 平面PBC,
∴AD∥平面PBC.
又∵平面ADMN∩平面PBC=MN,∴AD∥MN.
又∵BC∥AD,∴MN∥BC.
又∵N是PB的中点,∴点M为PC的中点.
∴MN∥BC且MN= BC,
又∵E为AD的中点, ∴MN∥DE且MN=DE.
∴四边形DENM为平行四边形.
∴EN∥DM,且DM 平面PDC. ∴EN∥平面PDC.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(2)BC⊥平面PEB;
[证明] ∵四边形ABCD是边长为2的菱形,
且∠BAD=60°,∴BE⊥AD.
又∵侧面PAD是正三角形,且E为中点,
∴PE⊥AD,又∵PE∩BE=E,
∴AD⊥平面PBE.
又∵AD∥BC,
∴BC⊥平面PEB.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(3)平面PBC⊥平面ADMN.
[证明] 由(2)知AD⊥平面PBE,又PB 平面PBE,
∴AD⊥PB.
又∵PA=AB,N为PB的中点,
∴AN⊥PB. 且AN∩AD=A,
∴PB⊥平面ADMN.
又∵PB 平面PBC.
∴平面PBC⊥平面ADMN.
总结提升
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
跟踪训练
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
求证:(1)PA⊥平面ABC;
(2)当E为△PBC的垂心时,△ABC是直角三角形.
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.求证:(1)PA⊥平面ABC;
证明:在平面ABC内任取一点D,
作DF⊥AC于点F,作DG⊥AB于点G.
∵平面PAC⊥平面ABC,且交线为AC,
∴DF⊥平面PAC.
∵PA 平面PAC,
∴DF⊥PA. 同理可证,DG⊥PA.
∵DG∩DF=D,
∴PA⊥平面ABC.
证明:连接BE并延长交PC于点H.
∵E是△PBC的垂心,∴PC⊥BH.
又∵AE是平面PBC的垂线,∴PC⊥AE.
∵BH∩AE=E,∴PC⊥平面ABE,∴PC⊥AB.
又∵PA⊥平面ABC,∴PA⊥AB.
∵PA∩PC=P,∴AB⊥平面PAC.
∴AB⊥AC,即△ABC是直角三角形.
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.求证:(2)当E为△PBC的垂心时,△ABC是直角三角形.
H
随堂检测
1.已知平面α⊥平面β,直线l⊥平面α,则l与β的位置关系是( )
A.垂直 B.平行 C.l β D.平行或l β
D
l∥β或l β
2.如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是________三角形.
设P在平面ABC上的射影为O,
∵平面PAB⊥底面ABC,平面PAB∩平面ABC=AB,
∴O∈AB.
∵PA=PB=PC,
∴OA=OB=OC,
∴O是△ABC的外心,且是AB的中点,
∴△ABC是直角三角形.
直角
3.如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PCD⊥平面ABCD.
求证:AD⊥平面PCD.
证明:在矩形ABCD中,AD⊥CD,
因为平面PCD⊥平面ABCD,
平面PCD∩平面ABCD=CD,
AD 平面ABCD,
所以AD⊥平面PCD.
本课小结
1. 平面与平面垂直的性质定理
两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.
2. 证明线面垂直的两种方法
线线垂直
线面垂直
面面垂直
线面垂直
3. 线线、线面、面面之间关系的转化是解决空间图形问题的重要思想方法
线线垂直
线面垂直
判定
面面垂直
判定
性质
通过本节课,你学会了什么?
8.6.3 平面与平面垂直(2)
高一
必修二
本节目标
1. 掌握面面垂直的性质定理,能应用定理证明垂直关系.
2. 理解线线垂直、线面垂直、面面垂直的转化关系
预习课本P159~161,思考并完成以下问题
1.平面与平面垂直的性质定理是什么?
2.两个平面互相垂直可以推出哪些结论?
课前预习
1.若平面α⊥平面β,平面β⊥平面γ,则( )
A.α∥γ B.α⊥γ
C.α与γ相交但不垂直 D.以上都有可能
α
β
γ
α∥γ
α
β
α⊥γ
γ
α
β
α与γ相交但不垂直
γ
D
课前小测
2.平面α⊥平面β,α∩β=l,m α,m⊥l,则( )
A.m∥β B.m β
C.m⊥β D.m与β相交但不一定垂直
α⊥β
α∩β=l
m α
m⊥l
m⊥β
C
3.若两个平面互相垂直,在第一个平面内的一条直线a垂直于第二个平面内的一条直线b,那么( )
A.直线a垂直于第二个平面
B.直线b垂直于第一个平面
C.直线a不一定垂直于第二个平面
D.过a的平面必垂直于过b的平面
直线a与直线b均不一定为两面的交线.
C
4.平面α⊥平面β,α∩β=l,n β,n⊥l,直线m⊥α,则直线m与n的位置关系是__________.
平行
α⊥β
α∩β=l
n β
n⊥l
n⊥α
m⊥α
m∥n
新课导入
上节课已学内容:
平面与平面垂直的判定定理
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
a
a
反过来,如果两个平面垂直,能推出什么结论?
新知探究
探究
如图,设,α∩β=a. 则β内任意一条直线b与a有什么位置关系?相应地, b与α有什么位置关系?为什么?
a
b
显然, b与a平行或相交.
当b∥a时, b∥α;
当b与a相交时, b与α也相交.
a
b
特别的,当ba时,如图,设b与a的交点为A,过点A在内作直线ca,则直线b,c所成的角就是二面角- a- β的平面角.
由知, b c.
又因为ba, a 和c是内的两条相交直线,所以b.
a
b
A
c
由此可以得到平面与平面垂直的性质定理.
1.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的______,那么这条直线与另一个平面垂直
符号语言 a⊥β
图形语言
作用 ①面面垂直 线面垂直
②作面的垂线
交线
2.对面面垂直的性质定理的理解
(1)定理成立的条件有三个
①两个平面互相垂直;
②直线在其中一个平面内;
③直线与两平面的交线垂直.
(2)定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
(3)已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线垂直.
探究
设平面,点P在平面内,过点P作平面β的垂线a,直线a与平面具有什么位置关系?
P
a
b
P
b
c
c
a
如图,设,过点P在平面内作直线b c,根据平面与平面垂直的性质定理, b .因为过一点有且只有一条直线与平面垂直,所以直线a与直线b重合,因此a .
平面与平面垂直的性质定理2
两平面垂直,过一个平面内一点,垂直于第二个平面的直线在第一个平面内.
a
P
a
c
题型突破
典例深度剖析 重点多维探究
题型一 利用面面垂直的性质定理证明垂直
[例1] 如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于平面ABCD.若G为AD边的中点.
求证:平面PBG⊥平面PAD.
[证明] ∵四边形ABCD是菱形,∠DAB=60°,
∴△ABD是正三角形.
∵G为AD边的中点,
∴BG⊥AD.
∵平面PAD⊥平面ABCD,BG 平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
∵BG 平面PBG,
∴平面PBG⊥平面PAD.
[例1] 如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于平面ABCD.若G为AD边的中点.
求证:平面PBG⊥平面PAD.
总结提升
应用面面垂直性质定理证明相关问题时,一般需要作辅助线——过其中一个平面内一点作交线的垂线,使之转化为线面垂直,然后,进一步转化为线线垂直.
应用面面垂直性质定理要注意的问题
跟踪训练
1. 如图所示,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面PBC.
求证:BC⊥AC.
证明:如图,在平面PAC内作AD⊥PC交PC于点D,
∵平面PAC⊥平面PBC,AD 平面PAC,
且AD⊥PC,平面PAC∩平面PBC=PC,
∴AD⊥平面PBC,又∵BC 平面PBC,∴AD⊥BC.
∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC,
∵AD∩PA=A,∴BC⊥平面PAC,
∵AC 平面PAC,∴BC⊥AC.
D
题型二 线线、线面、面面垂直的综合
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点.
求证:(1)EN∥平面PDC;
(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADMN.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(1)EN∥平面PDC;
[证明] ∵AD∥BC,BC 平面PBC,AD 平面PBC,
∴AD∥平面PBC.
又∵平面ADMN∩平面PBC=MN,∴AD∥MN.
又∵BC∥AD,∴MN∥BC.
又∵N是PB的中点,∴点M为PC的中点.
∴MN∥BC且MN= BC,
又∵E为AD的中点, ∴MN∥DE且MN=DE.
∴四边形DENM为平行四边形.
∴EN∥DM,且DM 平面PDC. ∴EN∥平面PDC.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(2)BC⊥平面PEB;
[证明] ∵四边形ABCD是边长为2的菱形,
且∠BAD=60°,∴BE⊥AD.
又∵侧面PAD是正三角形,且E为中点,
∴PE⊥AD,又∵PE∩BE=E,
∴AD⊥平面PBE.
又∵AD∥BC,
∴BC⊥平面PEB.
[例2] 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A,D,N三点的平面交PC于M,E为AD的中点. 求证:(3)平面PBC⊥平面ADMN.
[证明] 由(2)知AD⊥平面PBE,又PB 平面PBE,
∴AD⊥PB.
又∵PA=AB,N为PB的中点,
∴AN⊥PB. 且AN∩AD=A,
∴PB⊥平面ADMN.
又∵PB 平面PBC.
∴平面PBC⊥平面ADMN.
总结提升
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
跟踪训练
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
求证:(1)PA⊥平面ABC;
(2)当E为△PBC的垂心时,△ABC是直角三角形.
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.求证:(1)PA⊥平面ABC;
证明:在平面ABC内任取一点D,
作DF⊥AC于点F,作DG⊥AB于点G.
∵平面PAC⊥平面ABC,且交线为AC,
∴DF⊥平面PAC.
∵PA 平面PAC,
∴DF⊥PA. 同理可证,DG⊥PA.
∵DG∩DF=D,
∴PA⊥平面ABC.
证明:连接BE并延长交PC于点H.
∵E是△PBC的垂心,∴PC⊥BH.
又∵AE是平面PBC的垂线,∴PC⊥AE.
∵BH∩AE=E,∴PC⊥平面ABE,∴PC⊥AB.
又∵PA⊥平面ABC,∴PA⊥AB.
∵PA∩PC=P,∴AB⊥平面PAC.
∴AB⊥AC,即△ABC是直角三角形.
2. 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.求证:(2)当E为△PBC的垂心时,△ABC是直角三角形.
H
随堂检测
1.已知平面α⊥平面β,直线l⊥平面α,则l与β的位置关系是( )
A.垂直 B.平行 C.l β D.平行或l β
D
l∥β或l β
2.如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是________三角形.
设P在平面ABC上的射影为O,
∵平面PAB⊥底面ABC,平面PAB∩平面ABC=AB,
∴O∈AB.
∵PA=PB=PC,
∴OA=OB=OC,
∴O是△ABC的外心,且是AB的中点,
∴△ABC是直角三角形.
直角
3.如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PCD⊥平面ABCD.
求证:AD⊥平面PCD.
证明:在矩形ABCD中,AD⊥CD,
因为平面PCD⊥平面ABCD,
平面PCD∩平面ABCD=CD,
AD 平面ABCD,
所以AD⊥平面PCD.
本课小结
1. 平面与平面垂直的性质定理
两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.
2. 证明线面垂直的两种方法
线线垂直
线面垂直
面面垂直
线面垂直
3. 线线、线面、面面之间关系的转化是解决空间图形问题的重要思想方法
线线垂直
线面垂直
判定
面面垂直
判定
性质
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
