人教版(2019)数学必修第二册第九章统计章末复习课件(共29张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册第九章统计章末复习课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 638.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:03:18 | ||
图片预览





文档简介
(共29张PPT)
第九章 统计章末复习
高一
必修二
整理、分析
估计、推断
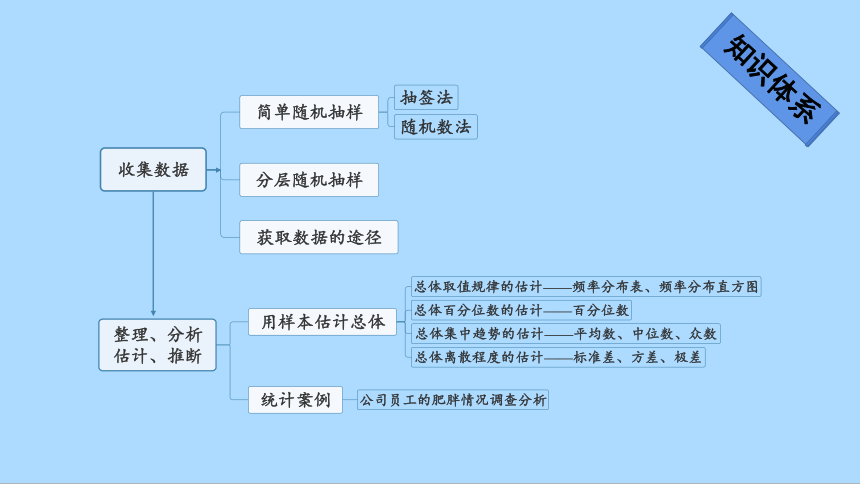
用样本估计总体
统计案例
总体取值规律的估计——频率分布表、频率分布直方图
总体百分位数的估计——百分位数
总体集中趋势的估计——平均数、中位数、众数
总体离散程度的估计——标准差、方差、极差
公司员工的肥胖情况调查分析
收集数据
简单随机抽样
分层随机抽样
获取数据的途径
抽签法
随机数法
知识体系
题型突破
典例深度剖析 重点多维探究
题型一 抽样方法的选取及应用
[例1] (1)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用比例分配的分层随机抽样方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
设从高二年级抽取的学生数为n,
分层随机抽样的原理是按照各部分在总体中所占的比例抽取样本.
则,解得n=8.
B
[例1] (2)问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:a.简单随机抽样;b.分层随机抽样.则问题与方法配对正确的顺序是________.
问题②中总体的个数较少,故可采用简单随机抽样.
问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法;
故匹配正确的顺序是b,a.
b,a
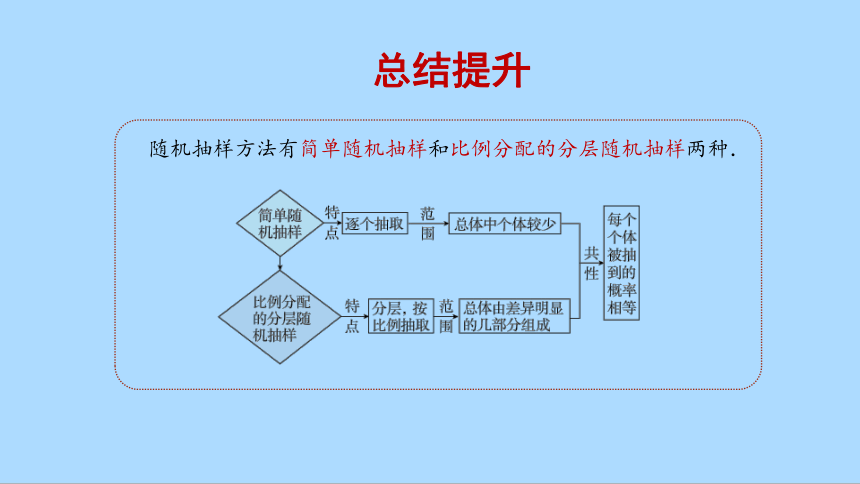
总结提升
随机抽样方法有简单随机抽样和比例分配的分层随机抽样两种.
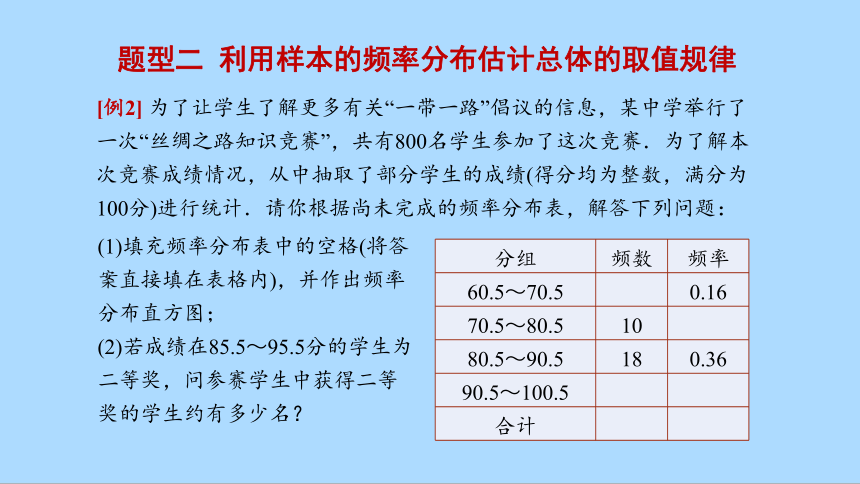
题型二 利用样本的频率分布估计总体的取值规律
[例2] 为了让学生了解更多有关“一带一路”倡议的信息,某中学举行了一次“丝绸之路知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
分组 频数 频率
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5 18 0.36
90.5~100.5
合计
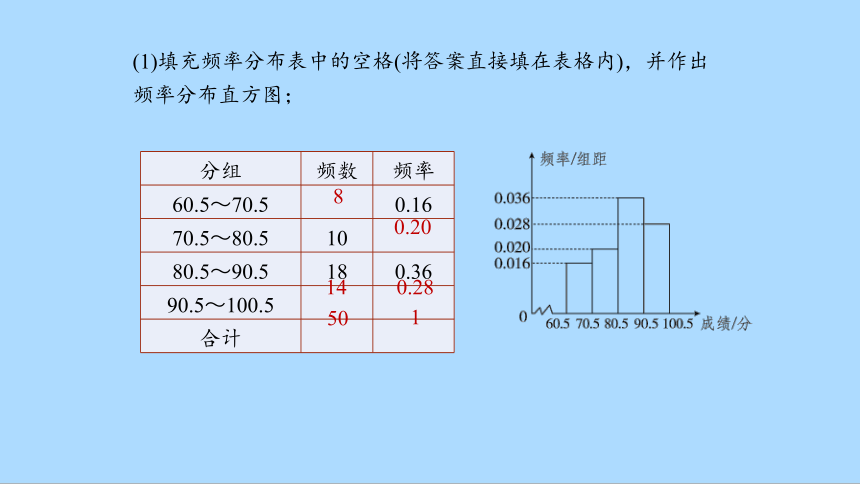
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图;
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
分组 频数 频率
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5 18 0.36
90.5~100.5
合计
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图;
8
14
0.20
0.28
50
1
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
所以获得二等奖的学生约有800×32%=256(名).
在被抽到的学生成绩中,在85.5~95.5分的个数是9+7=16,
占样本的比例是=0.32,
即获得二等奖的概率约为32%,
总结提升
要熟练掌握绘制统计图表的方法,
明确图表中有关数据的意义是正确分析问题的关键,
从图形与图表中获取有关信息并加以整理,
是近年来高考命题的热点.
利用统计表、统计图分析估计总体的分布规律
题型三 利用样本的百分位数估计总体的百分位数
[例3] 一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66 22.45 18.22 12.34
19.35 20.55 17.45 18.78 17.96 19.91 18.12 14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58 19.21 18.55 16.34
15.54 17.55 14.89 18.94 17.43 17.14 18.02 19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34 14.00 18.42 23.00
17.52 18.51 17.16 24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
将这50个样本数据按从小到大排序,可得
12.34 13.45 14.00 14.65 14.78 14.89 15.45 15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43 17.45 17.52
17.55 17.86 17.88 17.96 18.02 18.12 18.22 18.29 18.42
18.51 18.51 18.55 18.78 18.78 18.94 19.21 19.35 19.35
19.58 19.58 19.58 19.91 19.98 20.24 20.45 20.55 21.34
21.66 22.45 23.00 24.56 25.14
由65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
由50×(1-65%)=17.5可知这组数据的35%分位数为17.52.
总结提升
求一组数据的百分位数时,掌握其步骤:
①按照从小到大排列原始数据;
②计算i=n×p%;
③若i不是整数,大于i的最小整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为i项与第(i+1)项数据的平均数.
题型四 利用样本估计总体的集中趋势和离散程度
[例4] 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的中位数.
(1)求直方图中a的值;
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)组内的频率分别为0.08, 0.21, 0.25, 0.06, 0.04, 0.02.
由频率分布直方图,可知月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
由(1),100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12,
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300000×0.12=36000.
(3)估计居民月均用水量的中位数.
故可估计居民月均用水量的中位数为2.04吨.
设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,
所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
[例5] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如下图所示.
(1)填写下表:
平均数 方差 中位数 命中9环及以上
甲 7 1.2 1
乙 5.4 3
(2)请从四个不同的角度对这次测试进行分析:
①从平均数和方差结合分析偏离程度;
②从平均数和中位数结合分析谁的成绩好些;
③从平均数和命中9环以上的次数相结合看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
[例5] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如下图所示.
(1)填写下表:
平均数 方差 中位数 命中9环及以上
甲 7 1.2 1
乙 5.4 3
乙的射靶环数依次为2,4,6,8,7,7,8,9,9,10.
所以乙= ×(2+4+6+8+7+7+8+9+9+10)=7;
乙的射靶环数从小到大排列为2,4,6,7,7,8,8,9,9,10,
所以中位数是=7.5;
甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数为7.
7
7.5
7
(2)请从四个不同的角度对这次测试进行分析:
①从平均数和方差结合分析偏离程度;
甲、乙的平均数相同,均为7,但< ,
说明甲偏离平均数的程度小,而乙偏离平均数的程度大.甲比乙稳定些.
②从平均数和中位数结合分析谁的成绩好些;
甲、乙的平均水平相同,而乙的中位数比甲大,说明乙的射靶成绩比甲好些.
③从平均数和命中9环以上的次数相结合看谁的成绩好些;
甲、乙的平均水平相同,而乙命中9环以上(包含9环)的次数比甲多2次,可知乙的射靶成绩比甲好.
④从折线图上两人射击命中环数及走势分析谁更有潜力.
从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线上波动不大,说明乙的状态在提升,更有潜力.
总结提升
为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等对总体作出估计.众数就是样本数据中出现次数最多的那个值;中位数就是把样本数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,处于中间位置的数,如果数据的个数是偶数,中间两个数据的平均数;平均数就是所有样本数据的平均值,用表示;标准差是反映样本数据离散程度大小的最常用统计量,其计算公式是s= .有时也用标准差的平方s2——方差来代替标准差.
随堂检测
1.假设从高一年级全体同学(500人)中随机抽出60人参加一项活动,利用随机数法抽取样本时,先将500名同学按000,001,…,499进行编号,如果从随机数表第8行第11列的数开始,按三位数连续向右读取,最先抽出的5名同学的号码是(下面摘取了此随机数表第7行和第8行)( )
84421 75331 57245 50688 77047 44767 21763 35025 83921 20676
63016 37859 16955 56719 98105 07175 12867 35807 44395 23879
A.455 068 047 447 176
B.169 105 071 286 443
C.050 358 074 439 332
D.447 176 335 025 212
B
2.某学校三个兴趣小组的学生人数分布如下表(每名同学只参加一个小组)(单位:人).
篮球组 书画组 乐器组
高一 45 30 a
高二 15 10 20
学校要对这三个小组的活动效果进行抽样调查,按小组分层抽样的方法,从参加这三个兴趣小组的学生中抽取30人,结果篮球组被抽出12人,则a的值为________.
a=30
30
3.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
C
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
由已知得0.70=a+0.20+0.15,
故a=0.35,
b=1-0.05-0.15-0.70=0.10.
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
通过本节课,你学会了什么?
第九章 统计章末复习
高一
必修二
整理、分析
估计、推断
用样本估计总体
统计案例
总体取值规律的估计——频率分布表、频率分布直方图
总体百分位数的估计——百分位数
总体集中趋势的估计——平均数、中位数、众数
总体离散程度的估计——标准差、方差、极差
公司员工的肥胖情况调查分析
收集数据
简单随机抽样
分层随机抽样
获取数据的途径
抽签法
随机数法
知识体系
题型突破
典例深度剖析 重点多维探究
题型一 抽样方法的选取及应用
[例1] (1)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用比例分配的分层随机抽样方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
设从高二年级抽取的学生数为n,
分层随机抽样的原理是按照各部分在总体中所占的比例抽取样本.
则,解得n=8.
B
[例1] (2)问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:a.简单随机抽样;b.分层随机抽样.则问题与方法配对正确的顺序是________.
问题②中总体的个数较少,故可采用简单随机抽样.
问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法;
故匹配正确的顺序是b,a.
b,a
总结提升
随机抽样方法有简单随机抽样和比例分配的分层随机抽样两种.
题型二 利用样本的频率分布估计总体的取值规律
[例2] 为了让学生了解更多有关“一带一路”倡议的信息,某中学举行了一次“丝绸之路知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
分组 频数 频率
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5 18 0.36
90.5~100.5
合计
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图;
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
分组 频数 频率
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5 18 0.36
90.5~100.5
合计
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图;
8
14
0.20
0.28
50
1
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
所以获得二等奖的学生约有800×32%=256(名).
在被抽到的学生成绩中,在85.5~95.5分的个数是9+7=16,
占样本的比例是=0.32,
即获得二等奖的概率约为32%,
总结提升
要熟练掌握绘制统计图表的方法,
明确图表中有关数据的意义是正确分析问题的关键,
从图形与图表中获取有关信息并加以整理,
是近年来高考命题的热点.
利用统计表、统计图分析估计总体的分布规律
题型三 利用样本的百分位数估计总体的百分位数
[例3] 一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66 22.45 18.22 12.34
19.35 20.55 17.45 18.78 17.96 19.91 18.12 14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58 19.21 18.55 16.34
15.54 17.55 14.89 18.94 17.43 17.14 18.02 19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34 14.00 18.42 23.00
17.52 18.51 17.16 24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
将这50个样本数据按从小到大排序,可得
12.34 13.45 14.00 14.65 14.78 14.89 15.45 15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43 17.45 17.52
17.55 17.86 17.88 17.96 18.02 18.12 18.22 18.29 18.42
18.51 18.51 18.55 18.78 18.78 18.94 19.21 19.35 19.35
19.58 19.58 19.58 19.91 19.98 20.24 20.45 20.55 21.34
21.66 22.45 23.00 24.56 25.14
由65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
由50×(1-65%)=17.5可知这组数据的35%分位数为17.52.
总结提升
求一组数据的百分位数时,掌握其步骤:
①按照从小到大排列原始数据;
②计算i=n×p%;
③若i不是整数,大于i的最小整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为i项与第(i+1)项数据的平均数.
题型四 利用样本估计总体的集中趋势和离散程度
[例4] 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的中位数.
(1)求直方图中a的值;
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)组内的频率分别为0.08, 0.21, 0.25, 0.06, 0.04, 0.02.
由频率分布直方图,可知月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
由(1),100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12,
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300000×0.12=36000.
(3)估计居民月均用水量的中位数.
故可估计居民月均用水量的中位数为2.04吨.
设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,
所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
[例5] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如下图所示.
(1)填写下表:
平均数 方差 中位数 命中9环及以上
甲 7 1.2 1
乙 5.4 3
(2)请从四个不同的角度对这次测试进行分析:
①从平均数和方差结合分析偏离程度;
②从平均数和中位数结合分析谁的成绩好些;
③从平均数和命中9环以上的次数相结合看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
[例5] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如下图所示.
(1)填写下表:
平均数 方差 中位数 命中9环及以上
甲 7 1.2 1
乙 5.4 3
乙的射靶环数依次为2,4,6,8,7,7,8,9,9,10.
所以乙= ×(2+4+6+8+7+7+8+9+9+10)=7;
乙的射靶环数从小到大排列为2,4,6,7,7,8,8,9,9,10,
所以中位数是=7.5;
甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数为7.
7
7.5
7
(2)请从四个不同的角度对这次测试进行分析:
①从平均数和方差结合分析偏离程度;
甲、乙的平均数相同,均为7,但< ,
说明甲偏离平均数的程度小,而乙偏离平均数的程度大.甲比乙稳定些.
②从平均数和中位数结合分析谁的成绩好些;
甲、乙的平均水平相同,而乙的中位数比甲大,说明乙的射靶成绩比甲好些.
③从平均数和命中9环以上的次数相结合看谁的成绩好些;
甲、乙的平均水平相同,而乙命中9环以上(包含9环)的次数比甲多2次,可知乙的射靶成绩比甲好.
④从折线图上两人射击命中环数及走势分析谁更有潜力.
从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线上波动不大,说明乙的状态在提升,更有潜力.
总结提升
为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等对总体作出估计.众数就是样本数据中出现次数最多的那个值;中位数就是把样本数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,处于中间位置的数,如果数据的个数是偶数,中间两个数据的平均数;平均数就是所有样本数据的平均值,用表示;标准差是反映样本数据离散程度大小的最常用统计量,其计算公式是s= .有时也用标准差的平方s2——方差来代替标准差.
随堂检测
1.假设从高一年级全体同学(500人)中随机抽出60人参加一项活动,利用随机数法抽取样本时,先将500名同学按000,001,…,499进行编号,如果从随机数表第8行第11列的数开始,按三位数连续向右读取,最先抽出的5名同学的号码是(下面摘取了此随机数表第7行和第8行)( )
84421 75331 57245 50688 77047 44767 21763 35025 83921 20676
63016 37859 16955 56719 98105 07175 12867 35807 44395 23879
A.455 068 047 447 176
B.169 105 071 286 443
C.050 358 074 439 332
D.447 176 335 025 212
B
2.某学校三个兴趣小组的学生人数分布如下表(每名同学只参加一个小组)(单位:人).
篮球组 书画组 乐器组
高一 45 30 a
高二 15 10 20
学校要对这三个小组的活动效果进行抽样调查,按小组分层抽样的方法,从参加这三个兴趣小组的学生中抽取30人,结果篮球组被抽出12人,则a的值为________.
a=30
30
3.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
C
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
由已知得0.70=a+0.20+0.15,
故a=0.35,
b=1-0.05-0.15-0.70=0.10.
4. (全国卷Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
