人教版(2019)数学选择性必修一 1.1.2空间向量的数量积运算课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 1.1.2空间向量的数量积运算课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
空间向量的数量积运算
1.掌握空间向量夹角的概念及表示方法,掌握两个向量的数量积的概念、性质和计算方法及运算规律.
2.掌握两个向量的数量积的主要用途,会用它解决立体几何中一些简单的问题.
本节目标
预习课本P6~8,思考并完成以下问题
1.空间向量的数量积的定义是什么?
2.空间向量的数量积满足哪些运算律?
课前预习
课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)对于非零向量a,b,〈a,b〉与〈a,-b〉相等( )
(2)对于任意向量a,b,c,都有(a·b)c=a(b·c) ( )
(3)若a·b=b·c,且b≠0,则a=c( )
(4)(3a+2b)·(3a-2b)=9|a|2-4|b|2( )
×
×
×
√
2.已知正方体ABCD- A′B′C′D′的棱长为a,设=a, =b, =c,则〈 , 〉等于( )
A.30° B.60°
C.90° D.120°
D
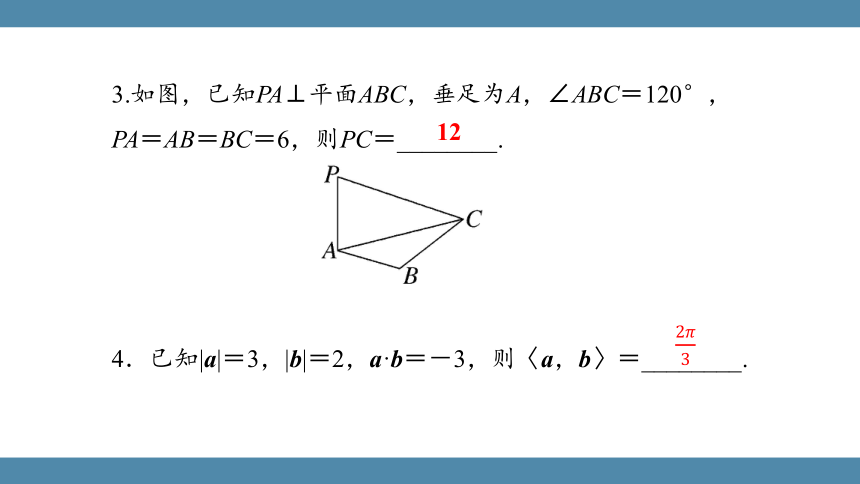
3.如图,已知PA⊥平面ABC,垂足为A,∠ABC=120°,PA=AB=BC=6,则PC=________.
12
4.已知|a|=3,|b|=2,a·b=-3,则〈a,b〉=________.
新知探究
1.空间向量的夹角
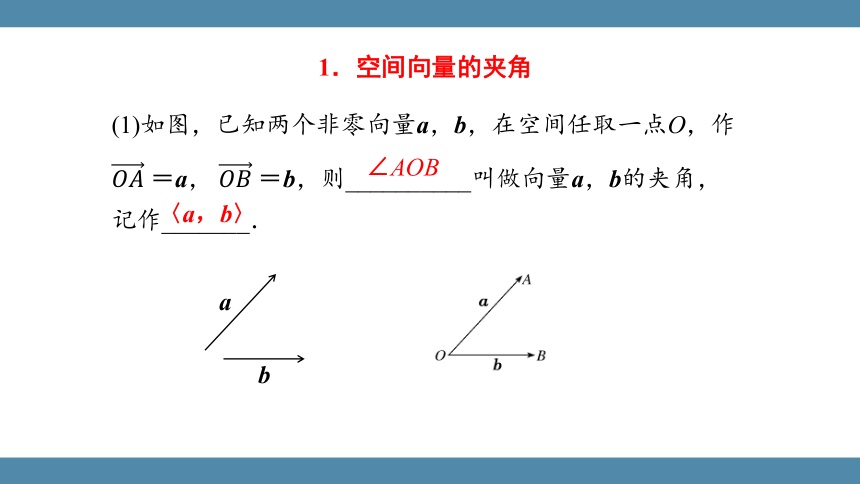
(1)如图,已知两个非零向量a,b,在空间任取一点O,作=a, =b,则__________叫做向量a,b的夹角,记作_______.
∠AOB
〈a,b〉
a
b
(2)向量a,b的夹角〈a,b〉的范围是_________,若〈a,b〉= ,那么称向量a,b互相________,记作_________.
[0,π]
垂直
a⊥b
a
b
a
b
O
A
B
空间向量的夹角与向量位置关系
(1)〈a,b〉=0时,向量a,b方向相同.
(2)〈a,b〉=π时,向量a,b方向相反.
(3)〈a,b〉=时,向量a⊥b.
知识点睛
2.空间向量的数量积
(1)定义
已知两个非零向量a,b,则_______________叫做a,b的数量积,记作a·b. 即a·b=_________________.
|a||b|cos〈a,b〉
|a||b|cos〈a,b〉
(2)运算律
①(λa)·b=______;
②交换律:a·b=______;
③分配律:a·(b+c)=__________.
λ(a·b)
b·a
a·b+a·c
3.空间向量数量积的性质
序号 性质
① a·e=|a|cos〈a,e〉(其中e为单位向量)
② 若a,b为非零向量,则a⊥b a·b=0
③ a·a=|a|2或|a|==
④ 若a,b为非零向量,则cos〈a,b〉=
⑤ |a·b|≤|a||b|(当且仅当a,b共线时等号成立)
注意:零向量与任意向量的数量积为0
(1)两个向量的数量积是数量,而不是向量,它可以是正数、负数或零;
(2)向量数量积的运算不满足消去律和乘法的结合律,即a·b=a·c b=c,(a·b)·c=a·(b·c)都不成立.
易错提示
题型突破
典例深度剖析 重点多维探究
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(1)
= ·
= ·cos〈 , 〉
= ×1×1×cos 60°= ,
所以= ;
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(2)
=··cos〈,〉= ×1×1×cos 0°= ,
所以= .
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(3)
=·=||·||·cos〈,〉= ×1×1×cos 120°=-,
所以=-
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(4)
=(+)· (+)
=[·(-)+ ·(-)+ · + · ]
=[-· - · +(-)· + · ]
= (-- + - + )=-.
由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.
方法总结
已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为________.
跟踪训练
-13
∵a+b+c=0
∴(a+b+c)2=0
∴a2+b2+c2+2(a·b+b·c+c·a)=0,
∴a·b+b·c+c·a=-13.
题型二 利用数量积求夹角
[例2] 如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
因为= - ,
所以· = · - ·
=||||cos〈,〉-||||cos〈,〉
=8×4×cos 135°-8×6×cos 120°=-16 +24.
所以cos〈 , 〉= = .
即OA与BC所成角的余弦值为.
利用向量的数量积,求异面直线所成的角的方法
(1)根据题设条件在所求的异面直线上取两个向量;
(2)将求异面直线所成角的问题转化为求向量夹角问题;
(3)利用向量的数量积求角的大小;
(4)证明两向量垂直可转化为数量积为零.
方法总结
如图所示,正四面体ABCD的每条棱长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.
跟踪训练
· =(+ + )· =(++ )·
=(+ + - )·
= a2+a2cos 120°+ a2cos 60°- a2cos 60°=0,
所以⊥ ,即MN⊥AB.同理可证MN⊥CD.
题型三 利用数量积求距离
[例3] 正三棱柱(底面是正三角形的直三棱柱)ABC-A1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.
如图所示,设=a,=b, =c.由题意知|a|=|b|=|c|=2,
且〈a,b〉=60°,〈a,c〉=〈b,c〉=90°.
因为= + + =-+ + =- a+ b+c,
EF2=||2= 2= a2+b2+c2+2
=1+1+4-1=5,
所以EF=.
利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量两两之间的夹角以及它们的模,利用公式|a|=求解即可.
方法总结
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
跟踪训练
随堂检测
1.若a,b均为非零向量,则a·b=|a||b|是a与b共线的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A
a·b=|a||b|cos〈a,b〉=|a||b| cos〈a,b〉=1 〈a,b〉=0,
当a与b反向时,不能成立.
2.已知a,b均为单位向量,它们的夹角为60°,那么|a-3b|等于( )
A. B.
C. D.4
∵|a-3b|2=(a-3b)2=a2-6a·b+9b2
=1-6×cos 60°+9=7.
∴|a-3b|= .
A
3.对于向量a、b、c和实数λ,下列命题中的真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
B
a⊥b a·b=0
×
|a|=|b|
×
a·(b-c)=0
×
√
4.设向量a,b满足|a+b|=,|a-b|=,则a·b等于( )
A.1 B.2 C.3 D.5
A
|a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,
将上面两式左、右两边分别相减,得4a·b=4,
∴a·b=1.
5.若向量a,b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|等于( )
A.2 B. C.1 D.
B
求空间向量的数量积要找到两个向量的模和夹角;
利用数量积求两异面直线所成的角,关键在于在异面直线上构造向量,找出两向量的关系;
证明两向量垂直可转化为证明两个向量的数量积为零,求线段长度转化为求向量的模.
本课小结
通过本节课,你学会了什么?
空间向量的数量积运算
1.掌握空间向量夹角的概念及表示方法,掌握两个向量的数量积的概念、性质和计算方法及运算规律.
2.掌握两个向量的数量积的主要用途,会用它解决立体几何中一些简单的问题.
本节目标
预习课本P6~8,思考并完成以下问题
1.空间向量的数量积的定义是什么?
2.空间向量的数量积满足哪些运算律?
课前预习
课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)对于非零向量a,b,〈a,b〉与〈a,-b〉相等( )
(2)对于任意向量a,b,c,都有(a·b)c=a(b·c) ( )
(3)若a·b=b·c,且b≠0,则a=c( )
(4)(3a+2b)·(3a-2b)=9|a|2-4|b|2( )
×
×
×
√
2.已知正方体ABCD- A′B′C′D′的棱长为a,设=a, =b, =c,则〈 , 〉等于( )
A.30° B.60°
C.90° D.120°
D
3.如图,已知PA⊥平面ABC,垂足为A,∠ABC=120°,PA=AB=BC=6,则PC=________.
12
4.已知|a|=3,|b|=2,a·b=-3,则〈a,b〉=________.
新知探究
1.空间向量的夹角
(1)如图,已知两个非零向量a,b,在空间任取一点O,作=a, =b,则__________叫做向量a,b的夹角,记作_______.
∠AOB
〈a,b〉
a
b
(2)向量a,b的夹角〈a,b〉的范围是_________,若〈a,b〉= ,那么称向量a,b互相________,记作_________.
[0,π]
垂直
a⊥b
a
b
a
b
O
A
B
空间向量的夹角与向量位置关系
(1)〈a,b〉=0时,向量a,b方向相同.
(2)〈a,b〉=π时,向量a,b方向相反.
(3)〈a,b〉=时,向量a⊥b.
知识点睛
2.空间向量的数量积
(1)定义
已知两个非零向量a,b,则_______________叫做a,b的数量积,记作a·b. 即a·b=_________________.
|a||b|cos〈a,b〉
|a||b|cos〈a,b〉
(2)运算律
①(λa)·b=______;
②交换律:a·b=______;
③分配律:a·(b+c)=__________.
λ(a·b)
b·a
a·b+a·c
3.空间向量数量积的性质
序号 性质
① a·e=|a|cos〈a,e〉(其中e为单位向量)
② 若a,b为非零向量,则a⊥b a·b=0
③ a·a=|a|2或|a|==
④ 若a,b为非零向量,则cos〈a,b〉=
⑤ |a·b|≤|a||b|(当且仅当a,b共线时等号成立)
注意:零向量与任意向量的数量积为0
(1)两个向量的数量积是数量,而不是向量,它可以是正数、负数或零;
(2)向量数量积的运算不满足消去律和乘法的结合律,即a·b=a·c b=c,(a·b)·c=a·(b·c)都不成立.
易错提示
题型突破
典例深度剖析 重点多维探究
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(1)
= ·
= ·cos〈 , 〉
= ×1×1×cos 60°= ,
所以= ;
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(2)
=··cos〈,〉= ×1×1×cos 0°= ,
所以= .
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(3)
=·=||·||·cos〈,〉= ×1×1×cos 120°=-,
所以=-
题型一 空间向量的数量积运算
[例1] 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(4)
=(+)· (+)
=[·(-)+ ·(-)+ · + · ]
=[-· - · +(-)· + · ]
= (-- + - + )=-.
由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.
方法总结
已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为________.
跟踪训练
-13
∵a+b+c=0
∴(a+b+c)2=0
∴a2+b2+c2+2(a·b+b·c+c·a)=0,
∴a·b+b·c+c·a=-13.
题型二 利用数量积求夹角
[例2] 如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
因为= - ,
所以· = · - ·
=||||cos〈,〉-||||cos〈,〉
=8×4×cos 135°-8×6×cos 120°=-16 +24.
所以cos〈 , 〉= = .
即OA与BC所成角的余弦值为.
利用向量的数量积,求异面直线所成的角的方法
(1)根据题设条件在所求的异面直线上取两个向量;
(2)将求异面直线所成角的问题转化为求向量夹角问题;
(3)利用向量的数量积求角的大小;
(4)证明两向量垂直可转化为数量积为零.
方法总结
如图所示,正四面体ABCD的每条棱长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.
跟踪训练
· =(+ + )· =(++ )·
=(+ + - )·
= a2+a2cos 120°+ a2cos 60°- a2cos 60°=0,
所以⊥ ,即MN⊥AB.同理可证MN⊥CD.
题型三 利用数量积求距离
[例3] 正三棱柱(底面是正三角形的直三棱柱)ABC-A1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.
如图所示,设=a,=b, =c.由题意知|a|=|b|=|c|=2,
且〈a,b〉=60°,〈a,c〉=〈b,c〉=90°.
因为= + + =-+ + =- a+ b+c,
EF2=||2= 2= a2+b2+c2+2
=1+1+4-1=5,
所以EF=.
利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量两两之间的夹角以及它们的模,利用公式|a|=求解即可.
方法总结
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
跟踪训练
随堂检测
1.若a,b均为非零向量,则a·b=|a||b|是a与b共线的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A
a·b=|a||b|cos〈a,b〉=|a||b| cos〈a,b〉=1 〈a,b〉=0,
当a与b反向时,不能成立.
2.已知a,b均为单位向量,它们的夹角为60°,那么|a-3b|等于( )
A. B.
C. D.4
∵|a-3b|2=(a-3b)2=a2-6a·b+9b2
=1-6×cos 60°+9=7.
∴|a-3b|= .
A
3.对于向量a、b、c和实数λ,下列命题中的真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
B
a⊥b a·b=0
×
|a|=|b|
×
a·(b-c)=0
×
√
4.设向量a,b满足|a+b|=,|a-b|=,则a·b等于( )
A.1 B.2 C.3 D.5
A
|a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,
将上面两式左、右两边分别相减,得4a·b=4,
∴a·b=1.
5.若向量a,b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|等于( )
A.2 B. C.1 D.
B
求空间向量的数量积要找到两个向量的模和夹角;
利用数量积求两异面直线所成的角,关键在于在异面直线上构造向量,找出两向量的关系;
证明两向量垂直可转化为证明两个向量的数量积为零,求线段长度转化为求向量的模.
本课小结
通过本节课,你学会了什么?
