人教版(2019)数学选择性必修一 1.2空间向量基本定理课件(共29张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 1.2空间向量基本定理课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:01:50 | ||
图片预览






文档简介
(共29张PPT)
空间向量基本定理
1.理解空间向量基本定理,并能用基本定理解决一些几何问题.
2.理解基底、基向量及向量的线性组合的概念.
本节目标
课前预习
空间向量基本定理的内容是什么?
(2) 在空间向量中,基底的定义是什么?应满足什么条件?
预习课本P11~14,思考并完成以下问题
课前小测
1. 关于空间向量的四个命题中正确的是( )
A.若,则P、A、B三点共线
B.若,则M、A、B 、C四点共面
C.△ABC为直角三角形的充要条件是
D.若为空间的一个基底,则构成空间的另一个基底
D
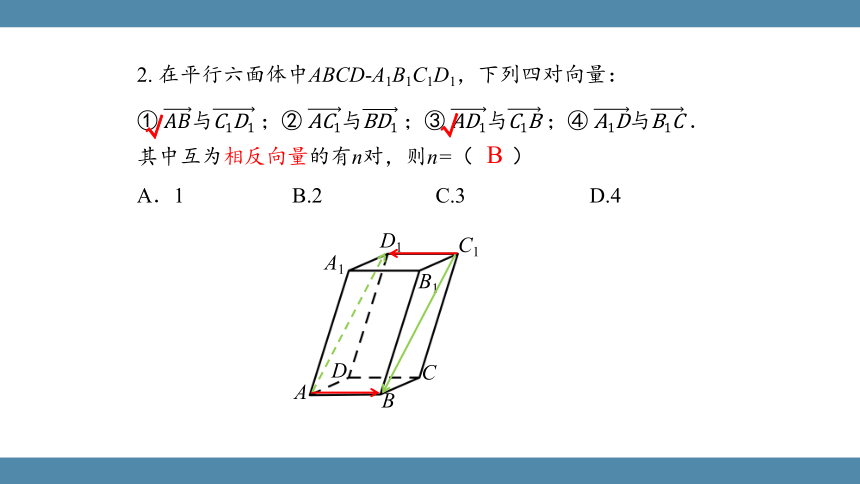
2. 在平行六面体中ABCD-A1B1C1D1,下列四对向量:
① 与;② 与;③ 与;④ 与.其中互为相反向量的有n对,则n=( )
A.1 B.2 C.3 D.4
A
B
C
D
A1
B1
C1
D1
√
√
B
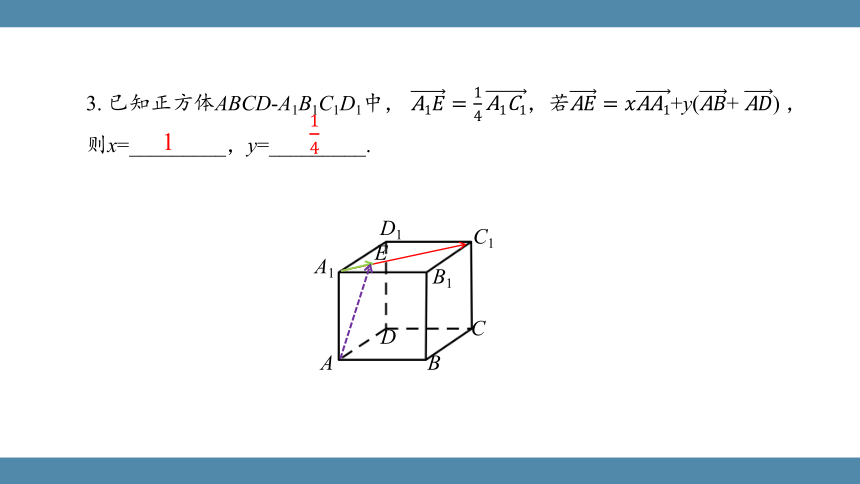
3. 已知正方体ABCD-A1B1C1D1中, ,若+y(+ ) ,则x=_________,y=_________.
1
A
B
C
D
A1
B1
C1
D1
E
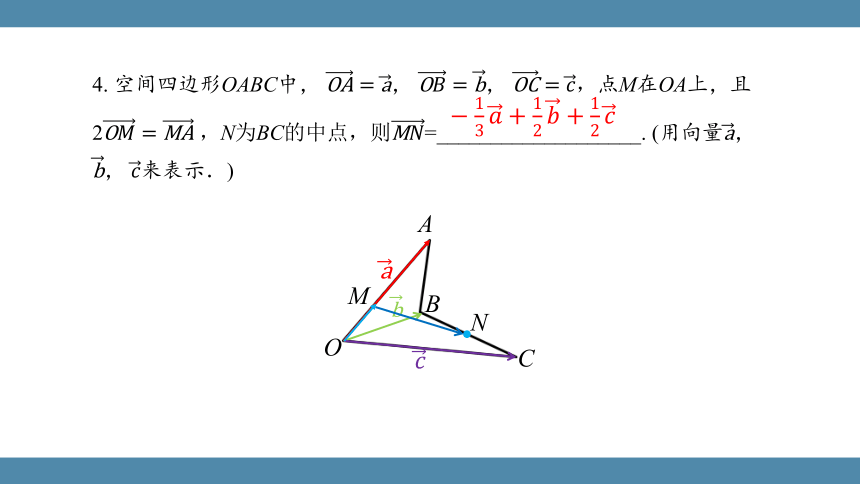
4. 空间四边形OABC中, , , 点M在OA上,且2 ,N为BC的中点,则=___________________. (用向量, , )
O
A
B
C
M
N
新知探究
1.空间向量基本定理
如果三个向量a,b,c_________,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
其中{a,b,c}叫做空间的一个_______,a,b,c都叫做_________.
不共面
基底
基向量
2. 向量的正交分解
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做_____________,常用{i,j,k}表示.
由空间向量基本定理可知,对空间中的任意向量a,均可以分解为三个向量xi、yj、zk,使a=xi+yj+zk. 像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行_________.
单位正交基底
正交分解
题型突破
典例深度剖析 重点多维探究
题型一 空间向量基本定理的理解
[例1] 已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3, =-3e1+e2+2e3, =e1+e2-e3,试判断{, ,}能否作为空间的一个基底?
判断给出的某一向量组能否作为基底,关键是要判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.
方法总结
判断基底的方法
跟踪训练
1. 设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下列向量组:
①{a,b,x};②{x,y,z};③{b,c,z};④{x,y,a+b+c}.
其中可以作为空间的基底的向量组有________个.
√
√
√
3
连接BO,则= = (+)= (c-b-a)=- a- b+ c.
=+=-a+ =-a+(+)=-a- b+ c.
=+=++(+)
=-a+c+ (-c+b)=-a+ b+ c.
= = = a.
题型二 用基底表示向量
[例2] 如图,四棱锥P- OABC 的底面为一矩形,PO⊥平面OABC,设=a, =b, =c,E,F分别是PC和PB的中点,试用a,b,c表示: , , , .
(1)若基底确定,要充分利用向量加法、减法的三角形法则和平行四边形法则,以及数乘向量的运算律进行.
(2)若没给定基底,首先选择基底,选择时,要尽量使所选的基向量能方便地表示其他向量,再就是看基向量的模及其夹角已知或易求.
解题策略
用基底表示向量的策略
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(1)用a,b,c表示向量, ;
=+=++=a+b+c.
=+= ++
=+-=b+c-a.
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示.
连接OG,OH,
则= + =- +
=-(+ )+ (+ )
=- (a+b+c+b)+ (a+b+c+c)= (c-b).
法一
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示.
法二
连接O′C,
则== (- )
= (c-b).
题型三 空间向量基本定理的应用
[例3] 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是边长为a的菱形,且∠C1CB=∠C1CD=∠BCD=60°,
(1)求证:C1C⊥BD;
· = ·(+ )= · + ·
=|| ||cos<, >+ || ||cos<, >
= ||(acos120°+acos60°) = 0
∴C1C⊥BD
题型三 空间向量基本定理的应用
[例3] 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是边长为a的菱形,且∠C1CB=∠C1CD=∠BCD=60°,
(2)当的值为多少时,能使A1C⊥平面C1BD?
由空间向量基本定理可知,如果把三个不共面的向量作为空间的一个基底,那么所有空间向量都可以用三个基向量表示出来. 进一步地,所有空间向量间的运算都可以转化为基向量间的运算,这为解决问题带来了方便.
解题策略
跟踪训练
3. 已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M、N分别是棱OA、BC的中点,求:直线MN与AC所成角的余弦值.
随堂检测
1.已知O,A,B,C为空间四个点,又为空间的一个基底,则( )
A.O,A,B,C四点共线
B.O,A,B,C四点共面
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
D
2.如图所示,在平行六面体中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且,设,用基底表示以下向量:
⑴ ;⑵ ;⑶ ;⑷ .
3. 对空间中一点P,满足条件,试判断:点P与是否一定共面?
由题意: ,
∴
∴ ,故向量共面,所以,点P与共面.
4.已知空间四边形OABC中,,
M、N分别是OA、BC的中点,G是MN的中点,求证OG⊥BC.
如图,连接ON,
设, , ,
则,
又
所以
所以
本课小结
1.空间向量基本定理的理解
2.用基底表示向量的策略
3.空间向量基本定理的应用
空间向量基本定理
1.理解空间向量基本定理,并能用基本定理解决一些几何问题.
2.理解基底、基向量及向量的线性组合的概念.
本节目标
课前预习
空间向量基本定理的内容是什么?
(2) 在空间向量中,基底的定义是什么?应满足什么条件?
预习课本P11~14,思考并完成以下问题
课前小测
1. 关于空间向量的四个命题中正确的是( )
A.若,则P、A、B三点共线
B.若,则M、A、B 、C四点共面
C.△ABC为直角三角形的充要条件是
D.若为空间的一个基底,则构成空间的另一个基底
D
2. 在平行六面体中ABCD-A1B1C1D1,下列四对向量:
① 与;② 与;③ 与;④ 与.其中互为相反向量的有n对,则n=( )
A.1 B.2 C.3 D.4
A
B
C
D
A1
B1
C1
D1
√
√
B
3. 已知正方体ABCD-A1B1C1D1中, ,若+y(+ ) ,则x=_________,y=_________.
1
A
B
C
D
A1
B1
C1
D1
E
4. 空间四边形OABC中, , , 点M在OA上,且2 ,N为BC的中点,则=___________________. (用向量, , )
O
A
B
C
M
N
新知探究
1.空间向量基本定理
如果三个向量a,b,c_________,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
其中{a,b,c}叫做空间的一个_______,a,b,c都叫做_________.
不共面
基底
基向量
2. 向量的正交分解
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做_____________,常用{i,j,k}表示.
由空间向量基本定理可知,对空间中的任意向量a,均可以分解为三个向量xi、yj、zk,使a=xi+yj+zk. 像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行_________.
单位正交基底
正交分解
题型突破
典例深度剖析 重点多维探究
题型一 空间向量基本定理的理解
[例1] 已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3, =-3e1+e2+2e3, =e1+e2-e3,试判断{, ,}能否作为空间的一个基底?
判断给出的某一向量组能否作为基底,关键是要判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.
方法总结
判断基底的方法
跟踪训练
1. 设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下列向量组:
①{a,b,x};②{x,y,z};③{b,c,z};④{x,y,a+b+c}.
其中可以作为空间的基底的向量组有________个.
√
√
√
3
连接BO,则= = (+)= (c-b-a)=- a- b+ c.
=+=-a+ =-a+(+)=-a- b+ c.
=+=++(+)
=-a+c+ (-c+b)=-a+ b+ c.
= = = a.
题型二 用基底表示向量
[例2] 如图,四棱锥P- OABC 的底面为一矩形,PO⊥平面OABC,设=a, =b, =c,E,F分别是PC和PB的中点,试用a,b,c表示: , , , .
(1)若基底确定,要充分利用向量加法、减法的三角形法则和平行四边形法则,以及数乘向量的运算律进行.
(2)若没给定基底,首先选择基底,选择时,要尽量使所选的基向量能方便地表示其他向量,再就是看基向量的模及其夹角已知或易求.
解题策略
用基底表示向量的策略
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(1)用a,b,c表示向量, ;
=+=++=a+b+c.
=+= ++
=+-=b+c-a.
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示.
连接OG,OH,
则= + =- +
=-(+ )+ (+ )
=- (a+b+c+b)+ (a+b+c+c)= (c-b).
法一
跟踪训练
2. 如图所示,正方体OABC- O′A′B′C′,且=a, =b, =c.
(2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示.
法二
连接O′C,
则== (- )
= (c-b).
题型三 空间向量基本定理的应用
[例3] 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是边长为a的菱形,且∠C1CB=∠C1CD=∠BCD=60°,
(1)求证:C1C⊥BD;
· = ·(+ )= · + ·
=|| ||cos<, >+ || ||cos<, >
= ||(acos120°+acos60°) = 0
∴C1C⊥BD
题型三 空间向量基本定理的应用
[例3] 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是边长为a的菱形,且∠C1CB=∠C1CD=∠BCD=60°,
(2)当的值为多少时,能使A1C⊥平面C1BD?
由空间向量基本定理可知,如果把三个不共面的向量作为空间的一个基底,那么所有空间向量都可以用三个基向量表示出来. 进一步地,所有空间向量间的运算都可以转化为基向量间的运算,这为解决问题带来了方便.
解题策略
跟踪训练
3. 已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M、N分别是棱OA、BC的中点,求:直线MN与AC所成角的余弦值.
随堂检测
1.已知O,A,B,C为空间四个点,又为空间的一个基底,则( )
A.O,A,B,C四点共线
B.O,A,B,C四点共面
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
D
2.如图所示,在平行六面体中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且,设,用基底表示以下向量:
⑴ ;⑵ ;⑶ ;⑷ .
3. 对空间中一点P,满足条件,试判断:点P与是否一定共面?
由题意: ,
∴
∴ ,故向量共面,所以,点P与共面.
4.已知空间四边形OABC中,,
M、N分别是OA、BC的中点,G是MN的中点,求证OG⊥BC.
如图,连接ON,
设, , ,
则,
又
所以
所以
本课小结
1.空间向量基本定理的理解
2.用基底表示向量的策略
3.空间向量基本定理的应用
