人教版(2019)数学选择性必修一 2.2.1直线的点斜式方程课件(共30张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 2.2.1直线的点斜式方程课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 913.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
直线的点斜式方程
1.理解直线的倾斜角和斜率的概念.
2.掌握求直线斜率的两种方法.
3.了解在平面直角坐标系中确定一条直线的几何要素.
本节目标
课前预习
预习课本P59~61,思考并完成以下问题
1.确定直线的几何要素是什么?
2.直线的点斜式方程是怎样推导的?
3.直线的点斜式方程与斜截式方程的结构形式分别是什么?
4.直线的纵截距是怎样定义的?
课前小测
1.直线的点斜式方程y-y0=k(x-x0)可以表示( )
A.任何一条直线
B.不过原点的直线
C.不与坐标轴垂直的直线
D.不与x轴垂直的直线
D
2.下面四个直线方程中,可以看作是直线的斜截式方程的是( )
A.x=3 B.2x+y-1=0
C.2y=x D.y=4x-1
D
3.已知直线l的点斜式方程为y-1=x-1,那么直线l的斜率为________,倾斜角为________,在y轴上的截距为________.
1
45°
0
新知探究
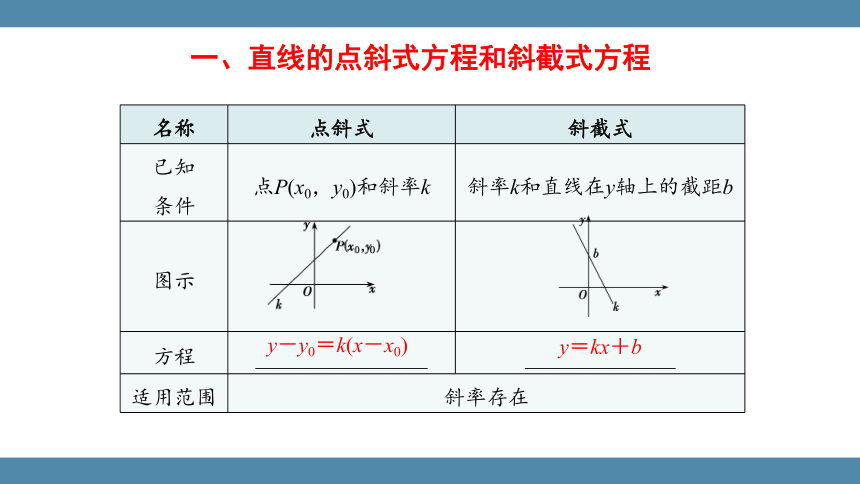
一、直线的点斜式方程和斜截式方程
名称 点斜式 斜截式
已知 条件 点P(x0,y0)和斜率k 斜率k和直线在y轴上的截距b
图示
方程 ________________ ______________
适用范围 斜率存在 y-y0=k(x-x0)
y=kx+b
二、直线l在y轴上的截距
直线l与y轴交点(0,b)的___________叫作直线l在y轴上的截距.
纵坐标b
定义
题型突破
典例深度剖析 重点多维探究
题型一 求直线的点斜式方程
[例1] (1)经过点(-5,2)且平行于y轴的直线方程为________.
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________.
(3)求过点P(1,2)且与直线y=2x+1平行的直线方程为________.
[例1] (1)经过点(-5,2)且平行于y轴的直线方程为________.
∵直线平行于y轴,∴直线不存在斜率,
∴方程为x=-5.
x=-5
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________________.
直线y=x+1的斜率k=1,所以倾斜角为45°.由题意知,直线l的倾斜角为135°,所以直线l的斜率k′=tan135°=-1,又点P(3,4)在直线l上,由点斜式方程知,直线l的方程为y-4=-(x-3).
y-4=-(x-3)
(3)求过点P(1,2)且与直线y=2x+1平行的
直线方程为___________.
由题意知,所求直线的斜率为2,且过点P(1,2),
∴直线方程为y-2=2(x-1),即2x-y=0.
2x-y=0
方法技巧
求直线的点斜式方程的方法步骤
跟踪训练
1.已知点A(3,3)和直线l:y=x-.求:
(1)过点A且与直线l平行的直线的点斜式方程;
(2)过点A且与直线l垂直的直线的点斜式方程.
题型二 求直线的斜截式方程
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
(3)经过点(3,4)且在两坐标轴上的截距相等.
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
y=2x+5
k=tan150°=-
y=-x-2
[例2] 根据条件写出下列直线的斜截式方程:
(3)经过点(3,4)且在两坐标轴上的截距相等.
设直线在两坐标轴上的截距为a,
当a=0时,直线的斜截式方程为y= x.
当a≠0时,设直线的斜截式方程为y=-x+b,
则有4=-3+b,即b=7.
此时方程为y=-x+7.
故所求直线方程为y= x或y=-x+7.
用斜截式求直线方程,只要确定直线的斜率和截距即可,同时要特别注意截距和距离的区别.
直线的斜截式方程y=kx+b不仅形式简单,而且特点明显,k是直线的斜率,b是直线在y轴上的截距,只要确定了k和b的值,直线的图象就一目了然.因此,在解决直线的图象问题时,常通过把直线方程化为斜截式方程,利用k,b的几何意义进行判断.
解题策略
直线的斜截式方程的求解策略
跟踪训练
2.已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.
题型三 利用直线的斜截式方程判断两直线位置关系
[例3] (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
[例3] (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
=-1, =a2-2,
故当a=-1时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行.
∵l1∥l2
∴ ,解得a=-1.
[例3] (2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
故当a=时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直.
=2a-1, =4
∵l1⊥l2
∴4(2a-1)=-1,解得a= .
不能用斜截式方程表示的直线,判断它们的位置关系时,需注意:
若两条直线的斜率均不存在,则有l1∥l2或l1与l2重合.
若一条直线的斜率不存在,另一条直线的斜率为0,则有l1⊥l2.
若一条直线的斜率不存在,另一条直线的斜率存在但不为0,则两条直线既不平行也不垂直.
易错提醒
跟踪训练
3.已知直线y=ax-2和y=(a+2)x+1互相垂直,则a=________.
-1
4.若直线l1:y=-x- 与直线l2:y=3x-1互相平行,则a=________.
-
随堂检测
1.直线y-b=2(x-a)在y轴上的截距为( )
A.a+b B.2a-b
C.b-2a D.|2a-b|
C
令x=0,得y=b-2a.
2.已知直线l过点(0,7),且与直线y=-4x+2平行,则直线l的方程为( )
A.y=-4x-7 B.y=4x-7
C.y=4x+7 D.y=-4x+7
D
3.直线y=k(x-2)+3必过定点,该定点坐标是________.
y-3 =k(x-2)
过定点(2,3)
(2,3)
1.建立点斜式方程的依据
直线上任一点与这条直线上一个定点的连线的斜率相同,故有=k,此式是不含点P1(x1,y1)的两条反向射线的方程,必须化为y-y1=k(x-x1)才是整条直线的方程.当直线的斜率不存在时,不能用点斜式表示,此时方程为x=x1.
本课小结
2.斜截式方程可看作点斜式的特殊情况,表示过(0,b)点、斜率为k的直线y-b=k(x-0),即y=kx+b,其特征是方程等号的一端只是一个y,其系数是1;等号的另一端是x的一次式,而不一定是x的一次函数.如y=c是直线的斜截式方程,而2y=3x+4不是直线的斜截式方程.
本课小结
直线的点斜式方程
1.理解直线的倾斜角和斜率的概念.
2.掌握求直线斜率的两种方法.
3.了解在平面直角坐标系中确定一条直线的几何要素.
本节目标
课前预习
预习课本P59~61,思考并完成以下问题
1.确定直线的几何要素是什么?
2.直线的点斜式方程是怎样推导的?
3.直线的点斜式方程与斜截式方程的结构形式分别是什么?
4.直线的纵截距是怎样定义的?
课前小测
1.直线的点斜式方程y-y0=k(x-x0)可以表示( )
A.任何一条直线
B.不过原点的直线
C.不与坐标轴垂直的直线
D.不与x轴垂直的直线
D
2.下面四个直线方程中,可以看作是直线的斜截式方程的是( )
A.x=3 B.2x+y-1=0
C.2y=x D.y=4x-1
D
3.已知直线l的点斜式方程为y-1=x-1,那么直线l的斜率为________,倾斜角为________,在y轴上的截距为________.
1
45°
0
新知探究
一、直线的点斜式方程和斜截式方程
名称 点斜式 斜截式
已知 条件 点P(x0,y0)和斜率k 斜率k和直线在y轴上的截距b
图示
方程 ________________ ______________
适用范围 斜率存在 y-y0=k(x-x0)
y=kx+b
二、直线l在y轴上的截距
直线l与y轴交点(0,b)的___________叫作直线l在y轴上的截距.
纵坐标b
定义
题型突破
典例深度剖析 重点多维探究
题型一 求直线的点斜式方程
[例1] (1)经过点(-5,2)且平行于y轴的直线方程为________.
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________.
(3)求过点P(1,2)且与直线y=2x+1平行的直线方程为________.
[例1] (1)经过点(-5,2)且平行于y轴的直线方程为________.
∵直线平行于y轴,∴直线不存在斜率,
∴方程为x=-5.
x=-5
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________________.
直线y=x+1的斜率k=1,所以倾斜角为45°.由题意知,直线l的倾斜角为135°,所以直线l的斜率k′=tan135°=-1,又点P(3,4)在直线l上,由点斜式方程知,直线l的方程为y-4=-(x-3).
y-4=-(x-3)
(3)求过点P(1,2)且与直线y=2x+1平行的
直线方程为___________.
由题意知,所求直线的斜率为2,且过点P(1,2),
∴直线方程为y-2=2(x-1),即2x-y=0.
2x-y=0
方法技巧
求直线的点斜式方程的方法步骤
跟踪训练
1.已知点A(3,3)和直线l:y=x-.求:
(1)过点A且与直线l平行的直线的点斜式方程;
(2)过点A且与直线l垂直的直线的点斜式方程.
题型二 求直线的斜截式方程
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
(3)经过点(3,4)且在两坐标轴上的截距相等.
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
y=2x+5
k=tan150°=-
y=-x-2
[例2] 根据条件写出下列直线的斜截式方程:
(3)经过点(3,4)且在两坐标轴上的截距相等.
设直线在两坐标轴上的截距为a,
当a=0时,直线的斜截式方程为y= x.
当a≠0时,设直线的斜截式方程为y=-x+b,
则有4=-3+b,即b=7.
此时方程为y=-x+7.
故所求直线方程为y= x或y=-x+7.
用斜截式求直线方程,只要确定直线的斜率和截距即可,同时要特别注意截距和距离的区别.
直线的斜截式方程y=kx+b不仅形式简单,而且特点明显,k是直线的斜率,b是直线在y轴上的截距,只要确定了k和b的值,直线的图象就一目了然.因此,在解决直线的图象问题时,常通过把直线方程化为斜截式方程,利用k,b的几何意义进行判断.
解题策略
直线的斜截式方程的求解策略
跟踪训练
2.已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.
题型三 利用直线的斜截式方程判断两直线位置关系
[例3] (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
[例3] (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
=-1, =a2-2,
故当a=-1时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行.
∵l1∥l2
∴ ,解得a=-1.
[例3] (2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
故当a=时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直.
=2a-1, =4
∵l1⊥l2
∴4(2a-1)=-1,解得a= .
不能用斜截式方程表示的直线,判断它们的位置关系时,需注意:
若两条直线的斜率均不存在,则有l1∥l2或l1与l2重合.
若一条直线的斜率不存在,另一条直线的斜率为0,则有l1⊥l2.
若一条直线的斜率不存在,另一条直线的斜率存在但不为0,则两条直线既不平行也不垂直.
易错提醒
跟踪训练
3.已知直线y=ax-2和y=(a+2)x+1互相垂直,则a=________.
-1
4.若直线l1:y=-x- 与直线l2:y=3x-1互相平行,则a=________.
-
随堂检测
1.直线y-b=2(x-a)在y轴上的截距为( )
A.a+b B.2a-b
C.b-2a D.|2a-b|
C
令x=0,得y=b-2a.
2.已知直线l过点(0,7),且与直线y=-4x+2平行,则直线l的方程为( )
A.y=-4x-7 B.y=4x-7
C.y=4x+7 D.y=-4x+7
D
3.直线y=k(x-2)+3必过定点,该定点坐标是________.
y-3 =k(x-2)
过定点(2,3)
(2,3)
1.建立点斜式方程的依据
直线上任一点与这条直线上一个定点的连线的斜率相同,故有=k,此式是不含点P1(x1,y1)的两条反向射线的方程,必须化为y-y1=k(x-x1)才是整条直线的方程.当直线的斜率不存在时,不能用点斜式表示,此时方程为x=x1.
本课小结
2.斜截式方程可看作点斜式的特殊情况,表示过(0,b)点、斜率为k的直线y-b=k(x-0),即y=kx+b,其特征是方程等号的一端只是一个y,其系数是1;等号的另一端是x的一次式,而不一定是x的一次函数.如y=c是直线的斜截式方程,而2y=3x+4不是直线的斜截式方程.
本课小结
