人教版(2019)数学选择性必修一 2_2_2直线的两点式方程 课件(共28张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 2_2_2直线的两点式方程 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
直线的两点式方程
1 .掌握直线的两点式方程.
2. 理解直线的截距式方程.
本节目标
课前预习
预习课本P62~64,思考并完成以下问题
1.直线的两点式方程的结构形式是什么?适用范围是什么?
2.直线的截距式方程的结构形式是什么?适用范围是什么?
课前小测
1.过点A(5,6)和点B(-1,2)的两点式方程是( )
A. = B. =
C. = D. =
B
2.在x轴,y轴上的截距分别为2,-3的直线方程为( )
A. -=1 B. +=1
C. -=1 D. +=0
A
3.直线-=1在两坐标轴上的截距之和为________.
-1
新知探究
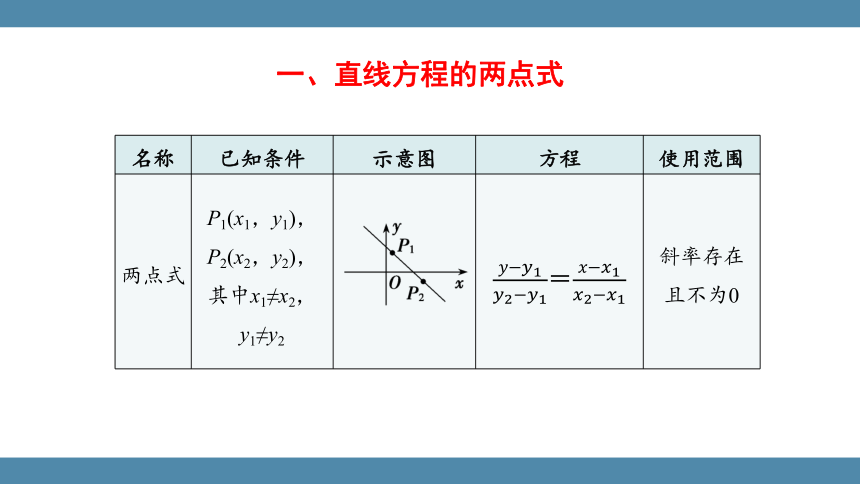
一、直线方程的两点式
名称 已知条件 示意图 方程 使用范围
两点式 P1(x1,y1), P2(x2,y2), 其中x1≠x2, y1≠y2 = 斜率存在
且不为0
二、直线方程的截距式
名称 已知条件 示意图 方程 使用范围
截距式 在x、y轴 上的截距 a、b且ab≠0 ___________
________________
直线l不过原点且不与坐标轴垂直
题型突破
典例深度剖析 重点多维探究
题型一 利用两点式求直线方程
[例1] 已知△ABC三个顶点坐标A(2,-1),B(2,2),C(4,1),求三角形三条边所在的直线方程.
∵A(2,-1),B(2,2),A,B两点横坐标相同,直线AB与x轴垂直,故其方程为x=2.
∵A(2,-1),C(4,1),由直线方程的两点式可得AC的方程为,即x-y-3=0.
题型一 利用两点式求直线方程
[例1] 已知△ABC三个顶点坐标A(2,-1),B(2,2),C(4,1),求三角形三条边所在的直线方程.
同理可由直线方程的两点式得直线BC的方程为
,即x+2y-6=0.
∴三边AB,AC,BC所在的直线方程分别为x=2,x-y-3=0,x+2y-6=0.
对直线的两点式方程的理解
(1)方程也可写成,两者形式有异但实质相同;
(2)当直线斜率不存在(x1=x2)或斜率为零(y1=y2)时,不能用两点式表示;
(3)如果将直线两点式转化为:(x2-x1)(y-y1)=(y2-y1)(x-x1),此时只要直线上两点不重合,都可以用它表示出来(即这个变形方程可以表示过任意已知两点的直线).
技法点拨
跟踪训练
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(1)求BC边的方程;
(2)求BC边上的中线所在直线的方程.
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(1)求BC边的方程;
∵BC边过两点B(5,-4),C(0,-2),
∴由两点式得,
即2x+5y+10=0.
故BC边的方程为2x+5y+10=0(0≤x≤5).
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(2)求BC边上的中线所在直线的方程.
设BC的中点为M(x0,y0),
则x0= = ,y0= =-3.
∴M(, -3),又BC边上的中线经过点A(-3,2).
∴由两点式得,即10x+11y+8=0.
故BC边上的中线所在直线的方程为10x+11y+8=0.
题型二 利用截距式求直线方程
[例2] (1)过点A(1,2),且在x轴上的截距和在y轴上的纵截距相等的直线方程是_________________.
分两种情形
若直线过原点,则方程为y=2x;
若直线不过原点,则可设直线的方程为+=1,将(1,2)代入,得a=3,则直线的方程为x+y=3.
y=2x或x+y=3
(2)一直线过点(-3,4),并且在两坐标轴上截距之和为12,这条直线方程是____________________________.
设直线的截距式方程为+=1
将点(-3,4)代入直线方程解得a=9或a=-4
故所求直线方程为x+3y-9=0或4x-y+16=0
x+3y-9=0或4x-y+16=0
(1)由截距式方程可直接确定直线与x轴和y轴的交点的坐标,因此用截距式画直线比较方便.
(2)在解决与截距有关或直线与坐标轴围成的三角形面积、周长等问题时,经常使用截距式.
(3)但当直线与坐标轴平行时,有一个截距不存在;当直线通过原点时,两个截距均为零.在这两种情况下都不能用截距式,故解决问题过程中要注意分类讨论.
用截距式方程解决问题的优点及注意事项
技法点拨
跟踪训练
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程.
(2)当△AOB的面积为6时,求直线l的方程.
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程.
设直线l的方程为+=1 (a>0,b>0),
由题意知,a+b+=12.
又因为直线l过点P,
所以+=1,即5a2-32a+48=0,
解得,
所以直线l的方程为3x+4y-12=0或15x+8y-36=0.
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(2)当△AOB的面积为6时,求直线l的方程.
设直线l的方程为+=1(a>0,b>0),
由题意知,ab=12,+=1,
消去b,得a2-6a+8=0,
解得,
所以直线l的方程为3x+4y-12=0或3x+y-6=0.
随堂检测
1.下列说法中正确的个数是( )
①经过定点P0(x0,y0)的直线都可以用y-y0=k(x-x0)来表示
②经过任意两点的直线都可以用(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示
③不经过原点的直线都可以用方程=1表示
④经过A(0,b)的直线都可以用方程y=kx+b表示
A.0 B.1 C.2 D.4
B
忽略了k不存在的情况
×
√
忽略了截距不存在的情况
×
忽略了k不存在的情况
×
2.过点P(-2,3)且在两坐标轴上的截距相等的直线l的方程为_____________________.
分两种情况:
(1)直线l过原点时,l的斜率为-,
∴直线方程为y=-x;
(2)l不过原点时,设方程为+=1,将x=-2,y=3代入得a=1,∴直线方程为x+y=1.
综上:l的方程为x+y-1=0或2y+3x=0.
x+y-1=0或2y+3x=0
3.求过点(1,1)且在y轴上的截距为在x轴上的截距的2倍的直线方程.
当a,b≠0时,设直线方程为+=1,由题可知+=1,且b=2a,解得a=,b=3,所以直线方程为+=1,即2x+y-3=0.
当a=b=0时,设y=kx,由题设可知,k=1,此时直线方程为y=x.
故所求直线方程为2x+y-3=0或x-y=0.
1.当直线没有斜率(x1=x2)或斜率为0(y1=y2)时,不能用两点式=求它的方程,此时直线的方程分别是x=x1和y=y1,而它们都适合(x2-x1)(y-y1)=(y2-y1)(x-x1),即两点式的整式形式,因此过任意两点的直线的方程都可以写成(x2-x1)(y-y1)=(y2-y1)(x-x1)的形式.
本课小结
2.直线的截距式是两点式的一个特殊情形,用它来画直线以及判断直线经过的象限或求直线与坐标轴围成的三角形的面积比较方便.注意直线过原点或与坐标轴平行时,没有截距式方程,但直线过原点时两截距存在且同时等于零.
本课小结
通过本节课,你学会了什么?
直线的两点式方程
1 .掌握直线的两点式方程.
2. 理解直线的截距式方程.
本节目标
课前预习
预习课本P62~64,思考并完成以下问题
1.直线的两点式方程的结构形式是什么?适用范围是什么?
2.直线的截距式方程的结构形式是什么?适用范围是什么?
课前小测
1.过点A(5,6)和点B(-1,2)的两点式方程是( )
A. = B. =
C. = D. =
B
2.在x轴,y轴上的截距分别为2,-3的直线方程为( )
A. -=1 B. +=1
C. -=1 D. +=0
A
3.直线-=1在两坐标轴上的截距之和为________.
-1
新知探究
一、直线方程的两点式
名称 已知条件 示意图 方程 使用范围
两点式 P1(x1,y1), P2(x2,y2), 其中x1≠x2, y1≠y2 = 斜率存在
且不为0
二、直线方程的截距式
名称 已知条件 示意图 方程 使用范围
截距式 在x、y轴 上的截距 a、b且ab≠0 ___________
________________
直线l不过原点且不与坐标轴垂直
题型突破
典例深度剖析 重点多维探究
题型一 利用两点式求直线方程
[例1] 已知△ABC三个顶点坐标A(2,-1),B(2,2),C(4,1),求三角形三条边所在的直线方程.
∵A(2,-1),B(2,2),A,B两点横坐标相同,直线AB与x轴垂直,故其方程为x=2.
∵A(2,-1),C(4,1),由直线方程的两点式可得AC的方程为,即x-y-3=0.
题型一 利用两点式求直线方程
[例1] 已知△ABC三个顶点坐标A(2,-1),B(2,2),C(4,1),求三角形三条边所在的直线方程.
同理可由直线方程的两点式得直线BC的方程为
,即x+2y-6=0.
∴三边AB,AC,BC所在的直线方程分别为x=2,x-y-3=0,x+2y-6=0.
对直线的两点式方程的理解
(1)方程也可写成,两者形式有异但实质相同;
(2)当直线斜率不存在(x1=x2)或斜率为零(y1=y2)时,不能用两点式表示;
(3)如果将直线两点式转化为:(x2-x1)(y-y1)=(y2-y1)(x-x1),此时只要直线上两点不重合,都可以用它表示出来(即这个变形方程可以表示过任意已知两点的直线).
技法点拨
跟踪训练
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(1)求BC边的方程;
(2)求BC边上的中线所在直线的方程.
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(1)求BC边的方程;
∵BC边过两点B(5,-4),C(0,-2),
∴由两点式得,
即2x+5y+10=0.
故BC边的方程为2x+5y+10=0(0≤x≤5).
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(2)求BC边上的中线所在直线的方程.
设BC的中点为M(x0,y0),
则x0= = ,y0= =-3.
∴M(, -3),又BC边上的中线经过点A(-3,2).
∴由两点式得,即10x+11y+8=0.
故BC边上的中线所在直线的方程为10x+11y+8=0.
题型二 利用截距式求直线方程
[例2] (1)过点A(1,2),且在x轴上的截距和在y轴上的纵截距相等的直线方程是_________________.
分两种情形
若直线过原点,则方程为y=2x;
若直线不过原点,则可设直线的方程为+=1,将(1,2)代入,得a=3,则直线的方程为x+y=3.
y=2x或x+y=3
(2)一直线过点(-3,4),并且在两坐标轴上截距之和为12,这条直线方程是____________________________.
设直线的截距式方程为+=1
将点(-3,4)代入直线方程解得a=9或a=-4
故所求直线方程为x+3y-9=0或4x-y+16=0
x+3y-9=0或4x-y+16=0
(1)由截距式方程可直接确定直线与x轴和y轴的交点的坐标,因此用截距式画直线比较方便.
(2)在解决与截距有关或直线与坐标轴围成的三角形面积、周长等问题时,经常使用截距式.
(3)但当直线与坐标轴平行时,有一个截距不存在;当直线通过原点时,两个截距均为零.在这两种情况下都不能用截距式,故解决问题过程中要注意分类讨论.
用截距式方程解决问题的优点及注意事项
技法点拨
跟踪训练
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程.
(2)当△AOB的面积为6时,求直线l的方程.
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程.
设直线l的方程为+=1 (a>0,b>0),
由题意知,a+b+=12.
又因为直线l过点P,
所以+=1,即5a2-32a+48=0,
解得,
所以直线l的方程为3x+4y-12=0或15x+8y-36=0.
2.直线l过点P,且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点.
(2)当△AOB的面积为6时,求直线l的方程.
设直线l的方程为+=1(a>0,b>0),
由题意知,ab=12,+=1,
消去b,得a2-6a+8=0,
解得,
所以直线l的方程为3x+4y-12=0或3x+y-6=0.
随堂检测
1.下列说法中正确的个数是( )
①经过定点P0(x0,y0)的直线都可以用y-y0=k(x-x0)来表示
②经过任意两点的直线都可以用(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示
③不经过原点的直线都可以用方程=1表示
④经过A(0,b)的直线都可以用方程y=kx+b表示
A.0 B.1 C.2 D.4
B
忽略了k不存在的情况
×
√
忽略了截距不存在的情况
×
忽略了k不存在的情况
×
2.过点P(-2,3)且在两坐标轴上的截距相等的直线l的方程为_____________________.
分两种情况:
(1)直线l过原点时,l的斜率为-,
∴直线方程为y=-x;
(2)l不过原点时,设方程为+=1,将x=-2,y=3代入得a=1,∴直线方程为x+y=1.
综上:l的方程为x+y-1=0或2y+3x=0.
x+y-1=0或2y+3x=0
3.求过点(1,1)且在y轴上的截距为在x轴上的截距的2倍的直线方程.
当a,b≠0时,设直线方程为+=1,由题可知+=1,且b=2a,解得a=,b=3,所以直线方程为+=1,即2x+y-3=0.
当a=b=0时,设y=kx,由题设可知,k=1,此时直线方程为y=x.
故所求直线方程为2x+y-3=0或x-y=0.
1.当直线没有斜率(x1=x2)或斜率为0(y1=y2)时,不能用两点式=求它的方程,此时直线的方程分别是x=x1和y=y1,而它们都适合(x2-x1)(y-y1)=(y2-y1)(x-x1),即两点式的整式形式,因此过任意两点的直线的方程都可以写成(x2-x1)(y-y1)=(y2-y1)(x-x1)的形式.
本课小结
2.直线的截距式是两点式的一个特殊情形,用它来画直线以及判断直线经过的象限或求直线与坐标轴围成的三角形的面积比较方便.注意直线过原点或与坐标轴平行时,没有截距式方程,但直线过原点时两截距存在且同时等于零.
本课小结
通过本节课,你学会了什么?
