人教版(2019)数学选择性必修一 2.2.3直线的一般式方程课件(共41张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 2.2.3直线的一般式方程课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:01:11 | ||
图片预览










文档简介
(共41张PPT)
直线的一般式方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系.
2.能正确地进行一般式方程与特殊形式的方程的转化.
3.能运用直线的一般式方程解决有关问题.
本节目标
课前预习
预习课本P64~66,思考并完成以下问题
1.怎样求一般式表示的直线的斜率与截距?
2.直线与二元一次方程之间的关系是怎样的?
课前小测
1.直线+=1化成一般式方程为( )
A.y=-x+4 B.y=-(x-3)
C.4x+3y-12=0 D.4x+3y+12=0
C
2.若直线l的一般式方程为2x-y+1=0,则直线l不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
3.与直线x+y-1=0垂直的直线的倾斜角为( )
A.30° B.60°
C.120° D.150°
B
新知探究
一、直线与二元一次方程的关系
在平面直角坐标系中的直线与二元一次方程的对应关系如下
直线
二元一次方程
一一对应
一一对应
关于x、y的二元一次方程________________;
二、直线的一般式方程
A、B______________.
Ax+By+C=0
不同时为零
式子
条件
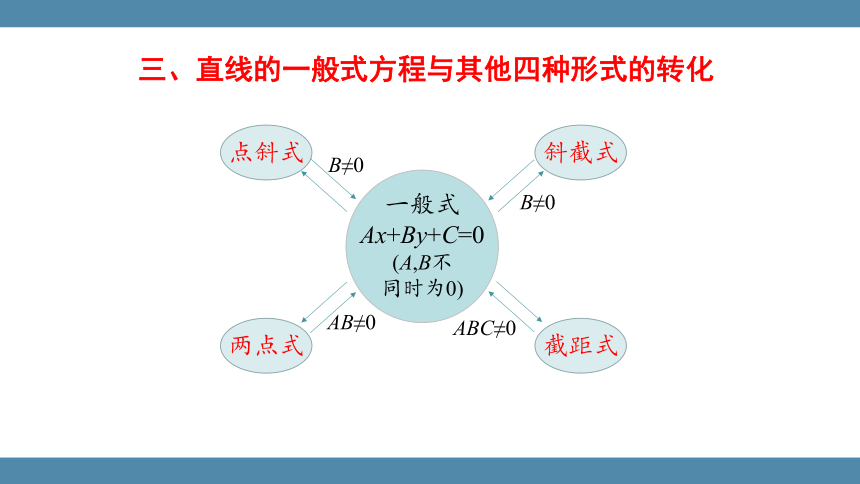
三、直线的一般式方程与其他四种形式的转化
一般式Ax+By+C=0
(A,B不
同时为0)
点斜式
斜截式
两点式
截距式
B≠0
B≠0
AB≠0
ABC≠0
题型突破
典例深度剖析 重点多维探究
题型一 求直线方程的一般式
[例1] 根据下列条件求解直线的一般式方程.
(1)直线的斜率为2,且经过点A(1,3);
(2)斜率为,且在y轴上的截距为4;
(3)经过两点A(2,-3),B(-1,-5);
(4)在x,y轴上的截距分别为2,-4.
[例1] 根据下列条件求解直线的一般式方程.
(1)直线的斜率为2,且经过点A(1,3);
因为k=2,且经过点A(1,3),
由直线的点斜式可得y-3=2(x-1),
整理可得2x-y+1=0,
所以直线的一般式方程为2x-y+1=0.
[例1] 根据下列条件求解直线的一般式方程.
(2)斜率为,且在y轴上的截距为4;
直线的斜率k=,且在y轴上的截距为4
直线的斜截式为y= x+4
整理可得直线的一般式方程为x-y+4=0
[例1] 根据下列条件求解直线的一般式方程.
(3)经过两点A(2,-3),B(-1,-5);
直线经过两点A(2,-3),B(-1,-5)
由直线的两点式可得,
整理得直线的一般式方程为2x-3y-13=0.
[例1] 根据下列条件求解直线的一般式方程.
(4)在x,y轴上的截距分别为2,-4.
由直线的截距式可得 +=1,
整理得直线的一般式方程为2x-y-4=0.
直线在x,y轴上的截距分别为2,-4
求直线方程的一般式,表面上需求A、B、C三个数,由于A、B不同时为零.
当A≠0时,方程可化为x+y+=0,只需求, 的值;
当B≠0时,方程可化为x+y+=0,只需确定, 的值.
因此,只要给出两个条件,就可以求出直线方程.
技法点拨
技法点拨
点斜式、斜截式方程不能表示斜率不存在的直线
两点式不能表示两点的横坐标相等、纵坐标相等的直线
截距式不能表示过原点及与坐标轴垂直的直线
一般式可以表示任何类型的直线而不受条件限制
解题策略
直线方程的其他形式都可以化成一般式,一般式也可以在适当条件下化成其他形式.
在求直线方程时,设一般式方程并不简单,常用的还是根据给定条件选用四种特殊形式之一求方程.
跟踪训练
1.根据下列各条件写出直线的方程,并且化成一般式.
(1)斜率是-,经过点A(8,-6)的直线方程为____________;
(2)经过点B(4,2),平行于x轴的直线方程为___________;
(3)在x轴和y轴上的截距分别是和-3的直线方程为____________;
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
x+y-1=0
x+2y+4=0
y-2=0
2x-y-3=0
题型二 一般式直线方程的综合应用
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
l的方程可化为y=-x+3,∴l的斜率为-.
∵l′与l平行,∴l′的斜率为-.
又∵l′过点(-1,3),
由点斜式知方程为y-3=- (x+1),
即3x+4y-9=0.
方法一
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(2)过点(-1,3),且与l垂直.
方法一
∵l′与l垂直
∴l′的斜率为
又l′过点(-1,3)
由点斜式可得方程为y-3= (x+1)
即4x-3y+13=0.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
方法二
由l′与l平行,可设l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9.
∴所求直线的方程为3x+4y-9=0.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(2)过点(-1,3),且与l垂直.
方法二
由l′与l垂直,可设l′的方程为4x-3y+n=0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13=0.
与直线Ax+By+C=0平行的直线方程可设为Ax+By+C1=0,再由其他条件列方程求出C1;
与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+C2=0,再由其他条件列方程求出C2.
技巧点拨
跟踪训练
2.(1)求与直线3x+4y+1=0平行且过点(1,2)的直线l的方程;
(2)求经过点A(2,1)且与直线2x+y-10=0垂直的直线l的方程.
题型三 由一般式直线方程判断位置关系
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
由l1:2x+(m+1)y+4=0,l2:mx+3y-2=0知:
①当m=0时,显然l1与l2不平行.
②当m≠0时,l1∥l2,需= ≠ .
解得m=2或m=-3,
∴m的值为2或-3.
方法一
[例3] (2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
方法一
由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a=-时,直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0,且2a+3≠0,则直线l1,l2的斜率k1,k2都存在,
k1=-,k2=-.
当l1⊥l2时,k1·k2=-1,即(-)·(-)=-1,∴a=-1.
综上可知,当a=1或a=-1时,直线l1⊥l2.
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
方法二
令2×3=m(m+1),解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2.
∴m的值为2或-3.
[例3] (2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
方法二
由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,
解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
(1)判定斜率是否存在,若存在,化成斜截式后,则k1=k2且b1≠b2;若都不存在,则还要判定不重合.
(2)可直接采用如下方法
一般地,设直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0,或A1C2-A2C1≠0.
这种判定方法避开了斜率存在和不存在两种情况的讨论,可以减小因考虑不周而造成失误的可能性.
方法总结
根据两直线的一般式方程判定两直线平行的方法
方法总结
若一个斜率为零,另一个不存在,则垂直;若两个都存在斜率,化成斜截式后,则k1k2=-1.
一般地,设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,l1⊥l2 A1A2+B1B2=0.
第二种方法可避免讨论,减小失误.
根据两直线的一般式方程判定两直线垂直的方法
跟踪训练
3.已知直线l1:2x+(λ+1)y-2=0,l2:λx+y-1=0,若l1∥l2,则λ的值是________.
因为l1∥l2,
所以2×1-(λ+1)λ=0,
即λ2+λ-2=0,解得λ=-2或λ=1.
当λ=1时,l1与l2重合,不符合题意.
所以λ=-2.
-2
随堂检测
1.已知直线x+y+1=0,则直线的倾斜角为( )
A.60° B.-60°
C.150° D.120°
D
2.直线y= x-2与两坐标轴围成的三角形的面积是________.
令x=0,得yA=-2;令y=0,得xB=3,
∴S△AOB= ×2×3=3.
3
3.与直线3x+4y+12=0平行,且与坐标轴构成的三角形的面积是24的直线l的方程是_____________________________.
设所求直线方程为3x+4y=a(a≠0),
则直线与两坐标轴的交点分别为(,0),(0, ),
∴ ×| |×| |=24,解得a=±24,
∴直线l的方程为3x+4y=±24.
3x+4y+24=0或3x+4y-24=0
在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的二元一次方程;
任何关于x,y的二元一次方程都表示一条直线.方程Ax+By+C=0(其中A、B不同时为0)叫做直线方程的一般式.
本课小结
本课小结
对于直线Ax+By+C=0
当B≠0时,其斜率为-,在y轴上的截距为-;
当B=0时,在x轴上的截距为-;
当AB≠0时,在两轴上的截距分别为-,-.
通过本节课,你掌握了哪些?
直线的一般式方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系.
2.能正确地进行一般式方程与特殊形式的方程的转化.
3.能运用直线的一般式方程解决有关问题.
本节目标
课前预习
预习课本P64~66,思考并完成以下问题
1.怎样求一般式表示的直线的斜率与截距?
2.直线与二元一次方程之间的关系是怎样的?
课前小测
1.直线+=1化成一般式方程为( )
A.y=-x+4 B.y=-(x-3)
C.4x+3y-12=0 D.4x+3y+12=0
C
2.若直线l的一般式方程为2x-y+1=0,则直线l不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
3.与直线x+y-1=0垂直的直线的倾斜角为( )
A.30° B.60°
C.120° D.150°
B
新知探究
一、直线与二元一次方程的关系
在平面直角坐标系中的直线与二元一次方程的对应关系如下
直线
二元一次方程
一一对应
一一对应
关于x、y的二元一次方程________________;
二、直线的一般式方程
A、B______________.
Ax+By+C=0
不同时为零
式子
条件
三、直线的一般式方程与其他四种形式的转化
一般式Ax+By+C=0
(A,B不
同时为0)
点斜式
斜截式
两点式
截距式
B≠0
B≠0
AB≠0
ABC≠0
题型突破
典例深度剖析 重点多维探究
题型一 求直线方程的一般式
[例1] 根据下列条件求解直线的一般式方程.
(1)直线的斜率为2,且经过点A(1,3);
(2)斜率为,且在y轴上的截距为4;
(3)经过两点A(2,-3),B(-1,-5);
(4)在x,y轴上的截距分别为2,-4.
[例1] 根据下列条件求解直线的一般式方程.
(1)直线的斜率为2,且经过点A(1,3);
因为k=2,且经过点A(1,3),
由直线的点斜式可得y-3=2(x-1),
整理可得2x-y+1=0,
所以直线的一般式方程为2x-y+1=0.
[例1] 根据下列条件求解直线的一般式方程.
(2)斜率为,且在y轴上的截距为4;
直线的斜率k=,且在y轴上的截距为4
直线的斜截式为y= x+4
整理可得直线的一般式方程为x-y+4=0
[例1] 根据下列条件求解直线的一般式方程.
(3)经过两点A(2,-3),B(-1,-5);
直线经过两点A(2,-3),B(-1,-5)
由直线的两点式可得,
整理得直线的一般式方程为2x-3y-13=0.
[例1] 根据下列条件求解直线的一般式方程.
(4)在x,y轴上的截距分别为2,-4.
由直线的截距式可得 +=1,
整理得直线的一般式方程为2x-y-4=0.
直线在x,y轴上的截距分别为2,-4
求直线方程的一般式,表面上需求A、B、C三个数,由于A、B不同时为零.
当A≠0时,方程可化为x+y+=0,只需求, 的值;
当B≠0时,方程可化为x+y+=0,只需确定, 的值.
因此,只要给出两个条件,就可以求出直线方程.
技法点拨
技法点拨
点斜式、斜截式方程不能表示斜率不存在的直线
两点式不能表示两点的横坐标相等、纵坐标相等的直线
截距式不能表示过原点及与坐标轴垂直的直线
一般式可以表示任何类型的直线而不受条件限制
解题策略
直线方程的其他形式都可以化成一般式,一般式也可以在适当条件下化成其他形式.
在求直线方程时,设一般式方程并不简单,常用的还是根据给定条件选用四种特殊形式之一求方程.
跟踪训练
1.根据下列各条件写出直线的方程,并且化成一般式.
(1)斜率是-,经过点A(8,-6)的直线方程为____________;
(2)经过点B(4,2),平行于x轴的直线方程为___________;
(3)在x轴和y轴上的截距分别是和-3的直线方程为____________;
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
x+y-1=0
x+2y+4=0
y-2=0
2x-y-3=0
题型二 一般式直线方程的综合应用
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
l的方程可化为y=-x+3,∴l的斜率为-.
∵l′与l平行,∴l′的斜率为-.
又∵l′过点(-1,3),
由点斜式知方程为y-3=- (x+1),
即3x+4y-9=0.
方法一
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(2)过点(-1,3),且与l垂直.
方法一
∵l′与l垂直
∴l′的斜率为
又l′过点(-1,3)
由点斜式可得方程为y-3= (x+1)
即4x-3y+13=0.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
方法二
由l′与l平行,可设l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9.
∴所求直线的方程为3x+4y-9=0.
[例2] 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(2)过点(-1,3),且与l垂直.
方法二
由l′与l垂直,可设l′的方程为4x-3y+n=0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13=0.
与直线Ax+By+C=0平行的直线方程可设为Ax+By+C1=0,再由其他条件列方程求出C1;
与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+C2=0,再由其他条件列方程求出C2.
技巧点拨
跟踪训练
2.(1)求与直线3x+4y+1=0平行且过点(1,2)的直线l的方程;
(2)求经过点A(2,1)且与直线2x+y-10=0垂直的直线l的方程.
题型三 由一般式直线方程判断位置关系
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
由l1:2x+(m+1)y+4=0,l2:mx+3y-2=0知:
①当m=0时,显然l1与l2不平行.
②当m≠0时,l1∥l2,需= ≠ .
解得m=2或m=-3,
∴m的值为2或-3.
方法一
[例3] (2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
方法一
由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a=-时,直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0,且2a+3≠0,则直线l1,l2的斜率k1,k2都存在,
k1=-,k2=-.
当l1⊥l2时,k1·k2=-1,即(-)·(-)=-1,∴a=-1.
综上可知,当a=1或a=-1时,直线l1⊥l2.
[例3] (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
方法二
令2×3=m(m+1),解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2.
∴m的值为2或-3.
[例3] (2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
方法二
由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,
解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
(1)判定斜率是否存在,若存在,化成斜截式后,则k1=k2且b1≠b2;若都不存在,则还要判定不重合.
(2)可直接采用如下方法
一般地,设直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0,或A1C2-A2C1≠0.
这种判定方法避开了斜率存在和不存在两种情况的讨论,可以减小因考虑不周而造成失误的可能性.
方法总结
根据两直线的一般式方程判定两直线平行的方法
方法总结
若一个斜率为零,另一个不存在,则垂直;若两个都存在斜率,化成斜截式后,则k1k2=-1.
一般地,设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,l1⊥l2 A1A2+B1B2=0.
第二种方法可避免讨论,减小失误.
根据两直线的一般式方程判定两直线垂直的方法
跟踪训练
3.已知直线l1:2x+(λ+1)y-2=0,l2:λx+y-1=0,若l1∥l2,则λ的值是________.
因为l1∥l2,
所以2×1-(λ+1)λ=0,
即λ2+λ-2=0,解得λ=-2或λ=1.
当λ=1时,l1与l2重合,不符合题意.
所以λ=-2.
-2
随堂检测
1.已知直线x+y+1=0,则直线的倾斜角为( )
A.60° B.-60°
C.150° D.120°
D
2.直线y= x-2与两坐标轴围成的三角形的面积是________.
令x=0,得yA=-2;令y=0,得xB=3,
∴S△AOB= ×2×3=3.
3
3.与直线3x+4y+12=0平行,且与坐标轴构成的三角形的面积是24的直线l的方程是_____________________________.
设所求直线方程为3x+4y=a(a≠0),
则直线与两坐标轴的交点分别为(,0),(0, ),
∴ ×| |×| |=24,解得a=±24,
∴直线l的方程为3x+4y=±24.
3x+4y+24=0或3x+4y-24=0
在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的二元一次方程;
任何关于x,y的二元一次方程都表示一条直线.方程Ax+By+C=0(其中A、B不同时为0)叫做直线方程的一般式.
本课小结
本课小结
对于直线Ax+By+C=0
当B≠0时,其斜率为-,在y轴上的截距为-;
当B=0时,在x轴上的截距为-;
当AB≠0时,在两轴上的截距分别为-,-.
通过本节课,你掌握了哪些?
