人教版(2019)数学选择性必修一 2.5.2圆与圆的位置关系课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 2.5.2圆与圆的位置关系课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
圆与圆的位置关系
1.了解两圆的五种位置关系.
2.掌握判断两圆位置关系的方法.
本节目标
课前预习
预习课本P96~97,思考并完成以下问题
1.圆与圆的位置关系有哪几种?它们分别怎样去判断?
2.两圆相交,怎样求公共弦所在的直线方程?
3.两圆相交,圆心连线与两圆的公共弦有什么关系?
课前小测
1.圆O1:x2+y2-2x=0和圆O2:x2+y2+4y=0的位置关系是( )
A.相离 B.外切
C.内切 D.相交
D
2.圆x2+y2=1与圆x2+y2+2x+2y+1=0的交点坐标为( )
A.(1,0)和(0,1) B.(1,0)和(0,-1)
C.(-1,0)和(0,-1) D.(-1,0)和(0,1)
C
3.圆x2+y2+4x-4y+7=0与圆x2+y2-4x+10y+13=0的公切线的条数是( )
A.1 B.2 C.3 D.4
D
新知探究
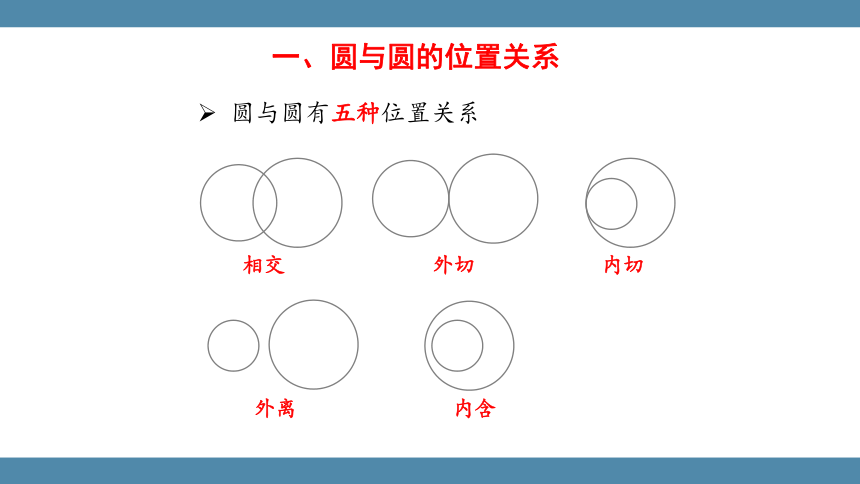
外离
外切
相交
内切
内含
一、圆与圆的位置关系
圆与圆有五种位置关系
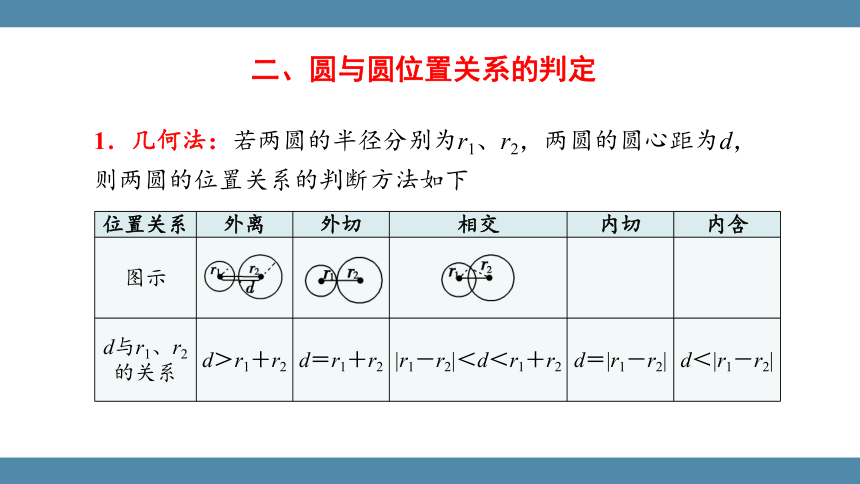
二、圆与圆位置关系的判定
1.几何法:若两圆的半径分别为r1、r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2 的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
2.代数法:联立两圆的方程组成方程组,则方程组解的个数与两圆的位置关系如下
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 外切或内切 外离或内含
题型突破
典例深度剖析 重点多维探究
题型一 两圆位置关系的判定
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(1)圆C1与圆C2外切;
(2)圆C1与圆C2内切.
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(1)圆C1与圆C2外切;
圆C1,圆C2的方程,经配方后为
C1:(x-m)2+(y+2)2=9;
C2:(x+1)2+(y-m)2=4,
其中C1(m,-2),C2(-1,m),r1=3,r2=2.
(1) 如果C1与C2外切,则有 =3+2,
即(m+1)2+(m+2)2=25.
∴m2+3m-10=0,解得m=-5或m=2.
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(2)圆C1与圆C2内切.
如果C1与C2内切,
则有 =3-2,
即(m+1)2+(m+2)2=1,
∴m2+3m+2=0,解得m=-2或m=-1.
∴当m=-5或m=2时,圆C1与圆C2外切;
当m=-2或m=-1时,圆C1与圆C2内切.
(1) 化成圆的标准方程,写出圆心和半径;
(2) 计算两圆圆心的距离d;
(3) 通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的值,必要时可借助于图形,数形结合.
1.判断两圆的位置关系或利用两圆的位置关系求参数有以下几个步骤:
2.应用几何法判定两圆的位置关系或求字母参数的范围是非常简单清晰的,要理清圆心距与两圆半径的关系.
技法总结
跟踪训练
1.集合A={(x,y)|x2+y2=4 },B={(x,y)|(x-3)2+(y-4)2=r2},其中r>0,若A∩B为只有一个元素的集合,则r的值为________.
两圆的位置关系为相切:内切或外切
当两圆内切时,|C1C2|=|r1-r2|,即5=|2-r|,又r>0,得r=7.
当两圆外切时,|C1C2|=|r1+r2|,即5=|2+r|,又r>0,得r=3.
两圆连心线的长为|C1C2|==5
故r的值为3或7.
3或7
题型二 与两圆相交有关的问题
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
x2+y2+6x-4=0
x2+y2+6y-28=0
得两圆的交点A(-1,3),B(-6,-2).
设所求圆的圆心为(a,b),因为圆心在直线x-y-4=0上,
故b=a-4.
则有,
解得a=,故圆心为,半径为 .
故圆的方程为,即x2+y2-x+7y-32=0.
解法一
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
圆x2+y2+6y-28=0的圆心(0,-3)不在直线x-y-4=0上,
可设所求圆的方程为x2+y2+6x-4+λ(x2+y2+6y-28)=0(λ≠-1),
其圆心为,
代入x-y-4=0,求得λ=-7.
故所求圆的方程为x2+y2-x+7y-32=0.
解法二
一般地过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0交点的圆的方程可设为:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1),然后再由其他条件求出λ,即可得圆的方程.
圆系方程
技法总结
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为
(D1-D2)x+(E1-E2)y+F1-F2=0.
两圆相交时,公共弦所在的直线方程
技法总结
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
公共弦长的求法
技法总结
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此为两圆公共弦所在直线的方程.
则A,B两点满足方程组
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
设两圆相交于点A,B,
解得或
所以|AB|= =,即公共弦长为.
解法一
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
解法二
由x2+y2-2x+10y-24=0,得(x-1)2+(y+5)2=50,
其圆心坐标为(1,-5),半径长r=5,
圆心到直线x-2y+4=0的距离为d= =3.
设公共弦长为2l,由勾股定理得r2=d2+l2,
即50=(3)2+l2,解得l=,
故公共弦长2l=2.
题型三 与两圆相切有关的问题
[例3] 求与圆x2+y2-2x=0外切且与直线x+y=0相切于点M(3,-)的圆的方程.
设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
则=r+1,①
= ,②
=r.③
联立①②③解得a=4,b=0,r=2,或a=0,b=-4,r=6,
即所求圆的方程为(x-4)2+y2=4或x2+(y+4)2=36.
则两圆相切
(1)设两圆的圆心分别为O1、O2,半径分别为r1、r2,
两圆相切时常用的性质
(2)两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦).
关键点拨
跟踪训练
3. 求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
设所求圆的圆心为P(a,b),则=1.①
(1)若两圆外切,则有=1+2=3,②
联立①②,解得a=5,b=-1,
所以,所求圆的方程为(x-5)2+(y+1)2=1;
(2)若两圆内切,则有=|2-1|=1,③
联立①③,解得a=3,b=-1,
所以,所求圆的方程为(x-3)2+(y+1)2=1.
综上所述,所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.
随堂检测
1.圆C1:x2+y2+4x-4y+7=0和圆C2:x2+y2-4x-10y+13=0的公切线有( )
A.1条 B.3条
C.4条 D.以上均不正确
∵C1(-2,2),r1=1,C2(2,5),r2=4,
∴|C1C2|=5=r1+r2,
∴两圆相外切,因此公切线有3条.
B
2.已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是( )
A.(x-5)2+(y-7)2=25
B.(x-5)2+(y-7)2=17或(x-5)2+(y+7)2=15
C.(x-5)2+(y-7)2=9
D.(x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
设动圆圆心为(x,y),
若动圆与已知圆外切,则=4+1,
∴(x-5)2+(y+7)2=25;
若动圆与已知圆内切,则=4-1,
∴(x-5)2+(y+7)2=9.
D
3.已知两圆x2+y2=10和(x-1)2+(y-3)2=20相交于A、B两点,则直线AB的方程是________.
x+3y=0
2x+6y=0
x+3y=0
1.两圆的位置关系有外离、外切、相交、内切、内含,判断直线与圆的位置关系的两种方法为代数法、几何法.
2.两圆相交时,公共弦所在的直线方程
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
本课小结
3.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
4. 两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦).
本课小结
通过本节课,你学会了什么?
圆与圆的位置关系
1.了解两圆的五种位置关系.
2.掌握判断两圆位置关系的方法.
本节目标
课前预习
预习课本P96~97,思考并完成以下问题
1.圆与圆的位置关系有哪几种?它们分别怎样去判断?
2.两圆相交,怎样求公共弦所在的直线方程?
3.两圆相交,圆心连线与两圆的公共弦有什么关系?
课前小测
1.圆O1:x2+y2-2x=0和圆O2:x2+y2+4y=0的位置关系是( )
A.相离 B.外切
C.内切 D.相交
D
2.圆x2+y2=1与圆x2+y2+2x+2y+1=0的交点坐标为( )
A.(1,0)和(0,1) B.(1,0)和(0,-1)
C.(-1,0)和(0,-1) D.(-1,0)和(0,1)
C
3.圆x2+y2+4x-4y+7=0与圆x2+y2-4x+10y+13=0的公切线的条数是( )
A.1 B.2 C.3 D.4
D
新知探究
外离
外切
相交
内切
内含
一、圆与圆的位置关系
圆与圆有五种位置关系
二、圆与圆位置关系的判定
1.几何法:若两圆的半径分别为r1、r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2 的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
2.代数法:联立两圆的方程组成方程组,则方程组解的个数与两圆的位置关系如下
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 外切或内切 外离或内含
题型突破
典例深度剖析 重点多维探究
题型一 两圆位置关系的判定
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(1)圆C1与圆C2外切;
(2)圆C1与圆C2内切.
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(1)圆C1与圆C2外切;
圆C1,圆C2的方程,经配方后为
C1:(x-m)2+(y+2)2=9;
C2:(x+1)2+(y-m)2=4,
其中C1(m,-2),C2(-1,m),r1=3,r2=2.
(1) 如果C1与C2外切,则有 =3+2,
即(m+1)2+(m+2)2=25.
∴m2+3m-10=0,解得m=-5或m=2.
[例1] 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为何值时,
(2)圆C1与圆C2内切.
如果C1与C2内切,
则有 =3-2,
即(m+1)2+(m+2)2=1,
∴m2+3m+2=0,解得m=-2或m=-1.
∴当m=-5或m=2时,圆C1与圆C2外切;
当m=-2或m=-1时,圆C1与圆C2内切.
(1) 化成圆的标准方程,写出圆心和半径;
(2) 计算两圆圆心的距离d;
(3) 通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的值,必要时可借助于图形,数形结合.
1.判断两圆的位置关系或利用两圆的位置关系求参数有以下几个步骤:
2.应用几何法判定两圆的位置关系或求字母参数的范围是非常简单清晰的,要理清圆心距与两圆半径的关系.
技法总结
跟踪训练
1.集合A={(x,y)|x2+y2=4 },B={(x,y)|(x-3)2+(y-4)2=r2},其中r>0,若A∩B为只有一个元素的集合,则r的值为________.
两圆的位置关系为相切:内切或外切
当两圆内切时,|C1C2|=|r1-r2|,即5=|2-r|,又r>0,得r=7.
当两圆外切时,|C1C2|=|r1+r2|,即5=|2+r|,又r>0,得r=3.
两圆连心线的长为|C1C2|==5
故r的值为3或7.
3或7
题型二 与两圆相交有关的问题
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
x2+y2+6x-4=0
x2+y2+6y-28=0
得两圆的交点A(-1,3),B(-6,-2).
设所求圆的圆心为(a,b),因为圆心在直线x-y-4=0上,
故b=a-4.
则有,
解得a=,故圆心为,半径为 .
故圆的方程为,即x2+y2-x+7y-32=0.
解法一
[例2] 求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点且圆心在直线x-y-4=0上的圆的方程.
圆x2+y2+6y-28=0的圆心(0,-3)不在直线x-y-4=0上,
可设所求圆的方程为x2+y2+6x-4+λ(x2+y2+6y-28)=0(λ≠-1),
其圆心为,
代入x-y-4=0,求得λ=-7.
故所求圆的方程为x2+y2-x+7y-32=0.
解法二
一般地过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0交点的圆的方程可设为:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1),然后再由其他条件求出λ,即可得圆的方程.
圆系方程
技法总结
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为
(D1-D2)x+(E1-E2)y+F1-F2=0.
两圆相交时,公共弦所在的直线方程
技法总结
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
公共弦长的求法
技法总结
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此为两圆公共弦所在直线的方程.
则A,B两点满足方程组
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
设两圆相交于点A,B,
解得或
所以|AB|= =,即公共弦长为.
解法一
跟踪训练
2.求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
解法二
由x2+y2-2x+10y-24=0,得(x-1)2+(y+5)2=50,
其圆心坐标为(1,-5),半径长r=5,
圆心到直线x-2y+4=0的距离为d= =3.
设公共弦长为2l,由勾股定理得r2=d2+l2,
即50=(3)2+l2,解得l=,
故公共弦长2l=2.
题型三 与两圆相切有关的问题
[例3] 求与圆x2+y2-2x=0外切且与直线x+y=0相切于点M(3,-)的圆的方程.
设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
则=r+1,①
= ,②
=r.③
联立①②③解得a=4,b=0,r=2,或a=0,b=-4,r=6,
即所求圆的方程为(x-4)2+y2=4或x2+(y+4)2=36.
则两圆相切
(1)设两圆的圆心分别为O1、O2,半径分别为r1、r2,
两圆相切时常用的性质
(2)两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦).
关键点拨
跟踪训练
3. 求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
设所求圆的圆心为P(a,b),则=1.①
(1)若两圆外切,则有=1+2=3,②
联立①②,解得a=5,b=-1,
所以,所求圆的方程为(x-5)2+(y+1)2=1;
(2)若两圆内切,则有=|2-1|=1,③
联立①③,解得a=3,b=-1,
所以,所求圆的方程为(x-3)2+(y+1)2=1.
综上所述,所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.
随堂检测
1.圆C1:x2+y2+4x-4y+7=0和圆C2:x2+y2-4x-10y+13=0的公切线有( )
A.1条 B.3条
C.4条 D.以上均不正确
∵C1(-2,2),r1=1,C2(2,5),r2=4,
∴|C1C2|=5=r1+r2,
∴两圆相外切,因此公切线有3条.
B
2.已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是( )
A.(x-5)2+(y-7)2=25
B.(x-5)2+(y-7)2=17或(x-5)2+(y+7)2=15
C.(x-5)2+(y-7)2=9
D.(x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
设动圆圆心为(x,y),
若动圆与已知圆外切,则=4+1,
∴(x-5)2+(y+7)2=25;
若动圆与已知圆内切,则=4-1,
∴(x-5)2+(y+7)2=9.
D
3.已知两圆x2+y2=10和(x-1)2+(y-3)2=20相交于A、B两点,则直线AB的方程是________.
x+3y=0
2x+6y=0
x+3y=0
1.两圆的位置关系有外离、外切、相交、内切、内含,判断直线与圆的位置关系的两种方法为代数法、几何法.
2.两圆相交时,公共弦所在的直线方程
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
本课小结
3.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
4. 两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦).
本课小结
通过本节课,你学会了什么?
