人教版(2019)数学选择性必修一1.1.1空间向量及其线性运算课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一1.1.1空间向量及其线性运算课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:07:26 | ||
图片预览







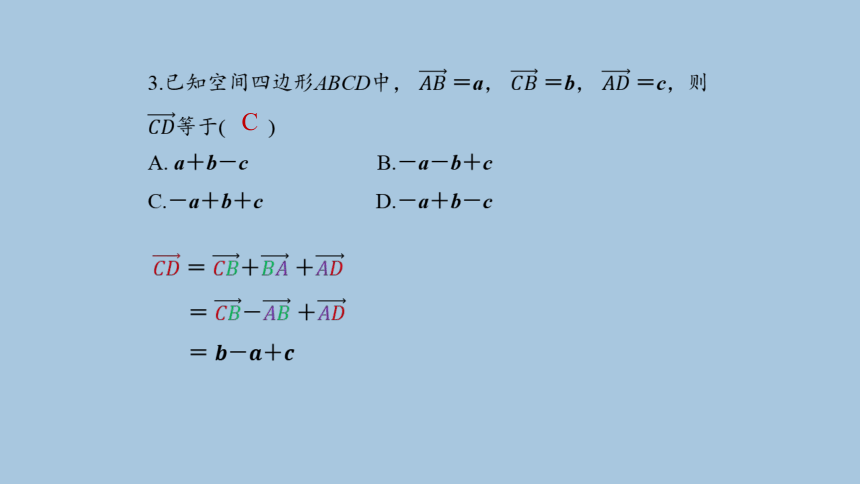


文档简介
(共34张PPT)
高二选择性必修一
1.1.1空间向量及其线性运算
本节目标
1.利用类比的方法理解空间向量的相关概念.
2.掌握空间向量的线性运算.
3.掌握共线向量定理和共面向量定理,并能熟练应用.
课前预习
1. 空间向量的概念及几类特殊向量
名称 定义
空间向量 在空间中,具有______和______的量叫做空间向量,向量的大小叫做向量的__________
单位向量 长度或模为______的向量
零向量 _________的向量
相等向量 方向______且模______的向量
相反向量 ______相反且______相等的向量
大小
方向
长度或模
1
长度为0
相同
相等
方向
模
2. 空间向量的表示
空间向量可以用a,b,c…表示,也用有向线段表示,有向线段的_______表示向量的模,向量a的起点是A,终点是B,则向量a也可记作,其模记为__________.
长度
|a|或||
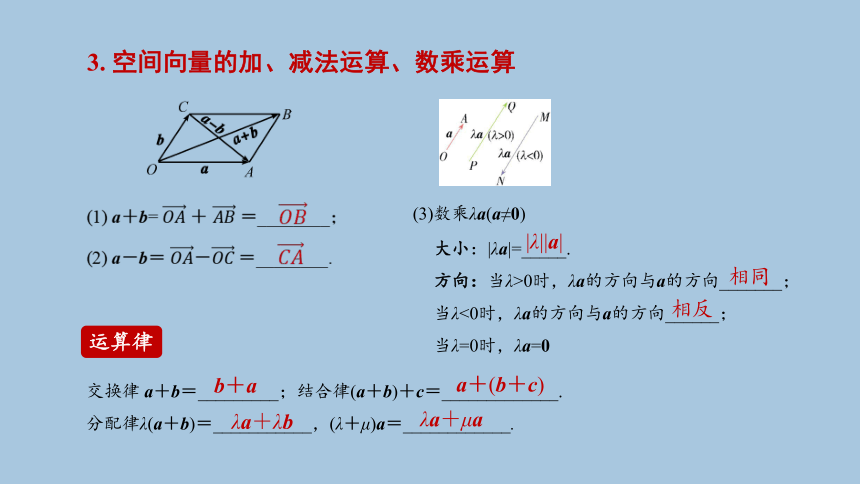
3. 空间向量的加、减法运算、数乘运算
(1) a+b= + =________;
(2) a-b= -=________.
交换律 a+b=_________;结合律(a+b)+c=_____________.
分配律λ(a+b)=___________,(λ+μ)a=____________.
大小:|λa|=_____.
方向:当λ>0时,λa的方向与a的方向_______;
当λ<0时,λa的方向与a的方向______;
当λ=0时,λa=0
(3)数乘λa(a≠0)
|λ||a|
相同
相反
运算律
b+a
a+(b+c)
λa+λb
λa+μa
4. 共线向量
(1)定义:表示空间向量的有向线段所在的直线_______________,则这些向量叫做____________或平行向量.
(2)共线向量定理:对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ使________.
互相平行或重合
共线向量
a=λb
5. 方向向量
在直线l上取非零向量a,我们把与向量a平行的_________成为直线l的方向向量.也就是说直线可以由其一点和它的方向向量确定.
非零向量
6. 共面向量
定义:平行于________________的向量叫做共面向量.
同一个平面
(1) =x +y ;
(2)对空间任一点O, = +x+y;
(3)对空间任一点O, =x+y+z(x+y+z=1);
(4) ∥(或∥,或∥).
①证明空间三个向量共面的常用方法
(1)设法证明其中一个向量可以表示成另两个向量的线性组合,即若a=xb+yc,则向量a,b,c共面;
(2)寻找平面α,证明这些向量与平面α平行.
②对空间四点P, M, A, B可通过证明下列结论成立来证明四点共面
小试牛刀
1.判断正错
(1)零向量没有方向.( )
(2)有向线段都可以表示向量,向量都可以用有向线段表示.( )
(3)平面内所有的单位向量是相等的.( )
(4)空间中,将单位向量起点放在一起,其终点组成的图形是球.( )
(5)任何两个向量均不可以比较大小( )
×
×
×
×
√
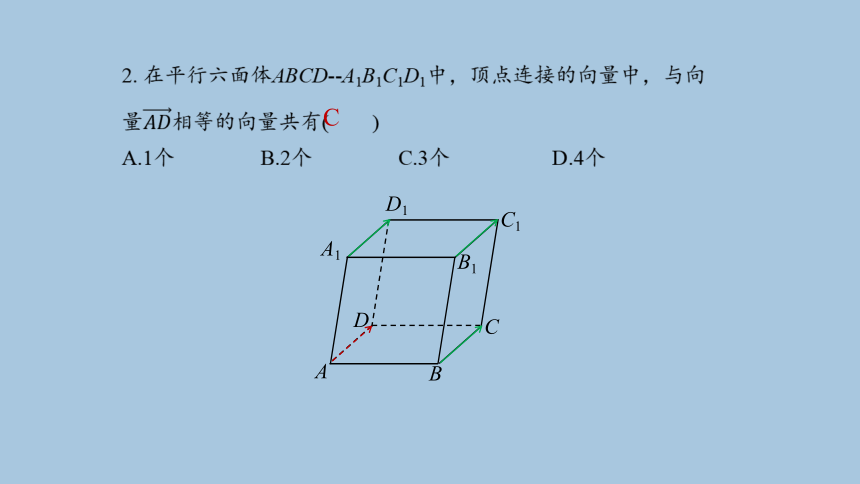
2. 在平行六面体ABCD -A1B1C1D1中,顶点连接的向量中,与向量相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
C
A
B
C
D
C1
D1
A1
B1
3.已知空间四边形ABCD中, =a, =b, =c,则等于( )
A. a+b-c B.-a-b+c
C.-a+b+c D.-a+b-c
C
= + +
= - +
= -+
典例剖析
题型
1
空间向量的概念
在空间中,向量、向量的模、相等向量的概念和平面中向量的相关概念完全一致.
注意
例1 给出下列命题:
①零向量没有确定的方向;
②在正方体ABCD- A1B1C1D1中, = ;
③若向量a与向量b的模相等,则a,b的方向相同或相反;
④在四边形ABCD中,必有+ =.
其中正确命题的序号是________.
典例剖析
题型
1
空间向量的概念
①②
√
√
×
a,b的方向不能确定
须是平行四边形
×
1. 下列关于空间向量的说法中正确的是( )
A.若向量a,b平行,则a,b所在直线平行
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
C.若向量,满足||>||,则>
D.相等向量其方向必相同
跟踪训练
向量a,b平行,则a,b所在的直线平行或重合
|a|=|b|只能说明a,b的长度相等而方向不确定
向量作为矢量不能比较大小
D
×
×
×
√
A
B
C
D
C'
D'
A'
B'
2.如图所示,在平行六面体ABCD-A′B′C′D′中,顶点连接的向量中,与向量相等的向量有_____________;与向量相反的向量有_________________.(要求写出所有适合条件的向量)
,
,
, , ,
题型
2
空间向量的线性运算
注意:
1.熟练掌握空间向量线性运算法则和运算律;
2.要注意数形结合思想的运用.
题型
2
空间向量的线性运算
例2 在如图所示的平行六面体中,求证:++=2 .
证明:∵平行六面体的六个面均为平行四边形,
∴=+ ,
=+ ,
=+
∴ ++=(+) +(+ ) +(+ )
=2(++ )
又∵ = ,
=
∴ ++ = ++
= +
=
∴ ++=2
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(1) =x +y +z ;
(2) =x +y +z .
跟踪训练
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(1) =x +y +z ;
所以x=1,y=-1,z=1.
=+
= ++
=-+ +
又 =x +y +z
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(2) =x +y +z .
所以x= ,y= ,z=1.
=+
=+
=+(+ )
= + +
= + +
又 =x +y +z ,
题型
3
向量的共线及判定
例3 如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且=2 ,F在对角线A1C上,且= ,求证:E,F,B三点共线.
注意
要证E,F,B三点共线,只需证明下面结论中的一个成立即可:
(1) =m;(2) = +λ ;
(3) =n +(1-n) .
例3 如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且=2 ,F在对角线A1C上,且= ,求证:E,F,B三点共线.
∴ = ,所以E,F,B三点共线.
证明:
设=a,=b, =c.
∵ =2 , = ,
∴ = , = .
∴ = = b,
= (- )= (+ - )= a+ b- c.
∴ = - = a- b- c= (a- b-c).
又= + + =- b-c+a=a- b-c,
跟踪训练
∴ = += (+),即与+共线.
解:连接AC,取AC的中点G,连接EG、FG,
∵E、F分别为AB、CD的中点.
∴ = , = .
又∵E、F、G三点共面,
在空间四边形ABCD中,E、F分别为AB、CD的中点,请判断与+ 是否共线.
题型
4
向量共面
例4 如图,已知四边形ABCD是平行四边形,点P是ABCD所在平面外的一点,连接PA,PB,PC,PD.设点E,F,G,H分别为△PAB,△PBC,△PCD,△PDA的重心.试用向量方法证明E,F,G,H四点共面.
所以= + ,由共面向量定理知,E,F,G,H四点共面.
证明:分别连接PE,PF,PG,PH并延长,交对边于点M,N,Q,R,
连接MN,NQ,QR,RM,
M
N
Q
R
因为点E,F,G,H分别是所在三角形的重心,所以M,N,Q,R是所在边的中点,
且= , = , = , = .
由题意知四边形MNQR是平行四边形,
所以= + =(- )+(- )= (- )+ (- ) = (+ ).
又= - = - = .
例4 如图,已知四边形ABCD是平行四边形,点P是ABCD所在平面外的一点,连接PA,PB,PC,PD.设点E,F,G,H分别为△PAB,△PBC,△PCD,△PDA的重心.试用向量方法证明E,F,G,H四点共面.
跟踪训练
又与不共线,根据向量共面的充要条件可知,, 共面.
因为M在BD上,且BM= BD,
所以= = + .
同理= + .
所以= + + =(+ )+ +(+ )= + = + .
如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM= BD,AN= AE.求证:向量,, 共面.
随堂检测
1.下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
②若向量,满足||>||,且与同向,则>;
③若两个非零向量与满足+=0,则,为相反向量;
④ =的充要条件是A与C重合,B与D重合.
其中错误的个数为( )
A.1 B.2 C.3 D.4
C
×
模相等且方向相同即为相等向量.
×
向量不能比较大小.
√
×
2.向量a,b互为相反向量,已知|b|=3,则下列结论正确的是( )
A.a=b B.a+b为实数0
C.a与b方向相同 D.|a|=3
向量a,b互为相反向量,则a,b模相等、方向相反
D
3.已知正方体ABCD-A1B1C1D1中, = ,若=x +y(+ ),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
=+
=+
=+(+ )
D
√
A
B
C
D
C1
D1
A1
B1
E
4.如图所示,空间四边形OABC中, =a, =b, =c,点M在OA上,且OM=2MA,N为BC中点,则等于( )
A. a- b+c B.-a+ b+ c
C. a+ b- c D.- a+b-c
= -
= ( + )-
= -a+ b+ c
B
5.如图,在长方体ABCD-A′B′C′D′中,AB=3,AD=2,AA′=1,则分别以长方体的顶点为起点和终点的向量中:
①单位向量共有多少个?
②试写出模为的所有向量.
③试写出与向量相等的所有向量.
④试写出向量的所有相反向量.
8个
= +
= +
= + ()
= + ()
= + [()]
= + +
= a + b + c
6.如图,已知空间四边形OABC,M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,设=a, =b, =c,试用a,b,c表示向量.
∴四边形EFGH是梯形.
7.如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且=, =.求证:四边形EFGH是梯形.
解:∵E,H分别是AB,AD的中点,
∴ =, = ,
则= -= -= = (- )= (-) = (-)= ,
∴ ∥且||= ||≠||.
又F不在直线EH上,
∴向量,,共面.
8.已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满足= + + .
(1)判断,,三个向量是否共面;
由已知,得+ + =3 ,
∴ - =(-)+(-),
∴ = + =--.
∴点M在平面ABC内.
8.已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满足= + + .
(2)判断点M是否在平面ABC内.
由(1)知,向量,,共面,
表示三个向量的有向线段又过同一点M,
∴M,A,B,C四点共面,
高二选择性必修一
1.1.1空间向量及其线性运算
本节目标
1.利用类比的方法理解空间向量的相关概念.
2.掌握空间向量的线性运算.
3.掌握共线向量定理和共面向量定理,并能熟练应用.
课前预习
1. 空间向量的概念及几类特殊向量
名称 定义
空间向量 在空间中,具有______和______的量叫做空间向量,向量的大小叫做向量的__________
单位向量 长度或模为______的向量
零向量 _________的向量
相等向量 方向______且模______的向量
相反向量 ______相反且______相等的向量
大小
方向
长度或模
1
长度为0
相同
相等
方向
模
2. 空间向量的表示
空间向量可以用a,b,c…表示,也用有向线段表示,有向线段的_______表示向量的模,向量a的起点是A,终点是B,则向量a也可记作,其模记为__________.
长度
|a|或||
3. 空间向量的加、减法运算、数乘运算
(1) a+b= + =________;
(2) a-b= -=________.
交换律 a+b=_________;结合律(a+b)+c=_____________.
分配律λ(a+b)=___________,(λ+μ)a=____________.
大小:|λa|=_____.
方向:当λ>0时,λa的方向与a的方向_______;
当λ<0时,λa的方向与a的方向______;
当λ=0时,λa=0
(3)数乘λa(a≠0)
|λ||a|
相同
相反
运算律
b+a
a+(b+c)
λa+λb
λa+μa
4. 共线向量
(1)定义:表示空间向量的有向线段所在的直线_______________,则这些向量叫做____________或平行向量.
(2)共线向量定理:对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ使________.
互相平行或重合
共线向量
a=λb
5. 方向向量
在直线l上取非零向量a,我们把与向量a平行的_________成为直线l的方向向量.也就是说直线可以由其一点和它的方向向量确定.
非零向量
6. 共面向量
定义:平行于________________的向量叫做共面向量.
同一个平面
(1) =x +y ;
(2)对空间任一点O, = +x+y;
(3)对空间任一点O, =x+y+z(x+y+z=1);
(4) ∥(或∥,或∥).
①证明空间三个向量共面的常用方法
(1)设法证明其中一个向量可以表示成另两个向量的线性组合,即若a=xb+yc,则向量a,b,c共面;
(2)寻找平面α,证明这些向量与平面α平行.
②对空间四点P, M, A, B可通过证明下列结论成立来证明四点共面
小试牛刀
1.判断正错
(1)零向量没有方向.( )
(2)有向线段都可以表示向量,向量都可以用有向线段表示.( )
(3)平面内所有的单位向量是相等的.( )
(4)空间中,将单位向量起点放在一起,其终点组成的图形是球.( )
(5)任何两个向量均不可以比较大小( )
×
×
×
×
√
2. 在平行六面体ABCD -A1B1C1D1中,顶点连接的向量中,与向量相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
C
A
B
C
D
C1
D1
A1
B1
3.已知空间四边形ABCD中, =a, =b, =c,则等于( )
A. a+b-c B.-a-b+c
C.-a+b+c D.-a+b-c
C
= + +
= - +
= -+
典例剖析
题型
1
空间向量的概念
在空间中,向量、向量的模、相等向量的概念和平面中向量的相关概念完全一致.
注意
例1 给出下列命题:
①零向量没有确定的方向;
②在正方体ABCD- A1B1C1D1中, = ;
③若向量a与向量b的模相等,则a,b的方向相同或相反;
④在四边形ABCD中,必有+ =.
其中正确命题的序号是________.
典例剖析
题型
1
空间向量的概念
①②
√
√
×
a,b的方向不能确定
须是平行四边形
×
1. 下列关于空间向量的说法中正确的是( )
A.若向量a,b平行,则a,b所在直线平行
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
C.若向量,满足||>||,则>
D.相等向量其方向必相同
跟踪训练
向量a,b平行,则a,b所在的直线平行或重合
|a|=|b|只能说明a,b的长度相等而方向不确定
向量作为矢量不能比较大小
D
×
×
×
√
A
B
C
D
C'
D'
A'
B'
2.如图所示,在平行六面体ABCD-A′B′C′D′中,顶点连接的向量中,与向量相等的向量有_____________;与向量相反的向量有_________________.(要求写出所有适合条件的向量)
,
,
, , ,
题型
2
空间向量的线性运算
注意:
1.熟练掌握空间向量线性运算法则和运算律;
2.要注意数形结合思想的运用.
题型
2
空间向量的线性运算
例2 在如图所示的平行六面体中,求证:++=2 .
证明:∵平行六面体的六个面均为平行四边形,
∴=+ ,
=+ ,
=+
∴ ++=(+) +(+ ) +(+ )
=2(++ )
又∵ = ,
=
∴ ++ = ++
= +
=
∴ ++=2
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(1) =x +y +z ;
(2) =x +y +z .
跟踪训练
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(1) =x +y +z ;
所以x=1,y=-1,z=1.
=+
= ++
=-+ +
又 =x +y +z
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,求下列各式中x,y,z的值.
(2) =x +y +z .
所以x= ,y= ,z=1.
=+
=+
=+(+ )
= + +
= + +
又 =x +y +z ,
题型
3
向量的共线及判定
例3 如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且=2 ,F在对角线A1C上,且= ,求证:E,F,B三点共线.
注意
要证E,F,B三点共线,只需证明下面结论中的一个成立即可:
(1) =m;(2) = +λ ;
(3) =n +(1-n) .
例3 如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且=2 ,F在对角线A1C上,且= ,求证:E,F,B三点共线.
∴ = ,所以E,F,B三点共线.
证明:
设=a,=b, =c.
∵ =2 , = ,
∴ = , = .
∴ = = b,
= (- )= (+ - )= a+ b- c.
∴ = - = a- b- c= (a- b-c).
又= + + =- b-c+a=a- b-c,
跟踪训练
∴ = += (+),即与+共线.
解:连接AC,取AC的中点G,连接EG、FG,
∵E、F分别为AB、CD的中点.
∴ = , = .
又∵E、F、G三点共面,
在空间四边形ABCD中,E、F分别为AB、CD的中点,请判断与+ 是否共线.
题型
4
向量共面
例4 如图,已知四边形ABCD是平行四边形,点P是ABCD所在平面外的一点,连接PA,PB,PC,PD.设点E,F,G,H分别为△PAB,△PBC,△PCD,△PDA的重心.试用向量方法证明E,F,G,H四点共面.
所以= + ,由共面向量定理知,E,F,G,H四点共面.
证明:分别连接PE,PF,PG,PH并延长,交对边于点M,N,Q,R,
连接MN,NQ,QR,RM,
M
N
Q
R
因为点E,F,G,H分别是所在三角形的重心,所以M,N,Q,R是所在边的中点,
且= , = , = , = .
由题意知四边形MNQR是平行四边形,
所以= + =(- )+(- )= (- )+ (- ) = (+ ).
又= - = - = .
例4 如图,已知四边形ABCD是平行四边形,点P是ABCD所在平面外的一点,连接PA,PB,PC,PD.设点E,F,G,H分别为△PAB,△PBC,△PCD,△PDA的重心.试用向量方法证明E,F,G,H四点共面.
跟踪训练
又与不共线,根据向量共面的充要条件可知,, 共面.
因为M在BD上,且BM= BD,
所以= = + .
同理= + .
所以= + + =(+ )+ +(+ )= + = + .
如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM= BD,AN= AE.求证:向量,, 共面.
随堂检测
1.下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
②若向量,满足||>||,且与同向,则>;
③若两个非零向量与满足+=0,则,为相反向量;
④ =的充要条件是A与C重合,B与D重合.
其中错误的个数为( )
A.1 B.2 C.3 D.4
C
×
模相等且方向相同即为相等向量.
×
向量不能比较大小.
√
×
2.向量a,b互为相反向量,已知|b|=3,则下列结论正确的是( )
A.a=b B.a+b为实数0
C.a与b方向相同 D.|a|=3
向量a,b互为相反向量,则a,b模相等、方向相反
D
3.已知正方体ABCD-A1B1C1D1中, = ,若=x +y(+ ),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
=+
=+
=+(+ )
D
√
A
B
C
D
C1
D1
A1
B1
E
4.如图所示,空间四边形OABC中, =a, =b, =c,点M在OA上,且OM=2MA,N为BC中点,则等于( )
A. a- b+c B.-a+ b+ c
C. a+ b- c D.- a+b-c
= -
= ( + )-
= -a+ b+ c
B
5.如图,在长方体ABCD-A′B′C′D′中,AB=3,AD=2,AA′=1,则分别以长方体的顶点为起点和终点的向量中:
①单位向量共有多少个?
②试写出模为的所有向量.
③试写出与向量相等的所有向量.
④试写出向量的所有相反向量.
8个
= +
= +
= + ()
= + ()
= + [()]
= + +
= a + b + c
6.如图,已知空间四边形OABC,M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,设=a, =b, =c,试用a,b,c表示向量.
∴四边形EFGH是梯形.
7.如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且=, =.求证:四边形EFGH是梯形.
解:∵E,H分别是AB,AD的中点,
∴ =, = ,
则= -= -= = (- )= (-) = (-)= ,
∴ ∥且||= ||≠||.
又F不在直线EH上,
∴向量,,共面.
8.已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满足= + + .
(1)判断,,三个向量是否共面;
由已知,得+ + =3 ,
∴ - =(-)+(-),
∴ = + =--.
∴点M在平面ABC内.
8.已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满足= + + .
(2)判断点M是否在平面ABC内.
由(1)知,向量,,共面,
表示三个向量的有向线段又过同一点M,
∴M,A,B,C四点共面,
