人教版(2019)数学选择性必修一 3_2_1双曲线及其标准方程 课件(共41张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 3_2_1双曲线及其标准方程 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 340.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:08:53 | ||
图片预览











文档简介
双曲线及其标准方程
1.了解双曲线的定义、几何图形和标准方程的推导过程.
2.掌握双曲线的标准方程.
3.会利用双曲线的定义和标准方程解决简单的应用问题.
本节目标
课前预习
预习课本P118~121,思考并完成以下问题
1.平面内满足什么条件的点的轨迹是双曲线?双曲线的焦点、焦距分别是什么?
2.什么是双曲线的标准方程?
课前小测
(3)双曲线标准方程中,a,b的大小关系是a>b. ( )
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
(2)在双曲线标准方程????2????2?????2????2?=1中,a>0,b>0且a≠b. ( )
?
×
×
×
2.已知双曲线????216?????29?=1,则双曲线的焦点坐标为( )
A.(-7?, 0),(7, 0) B.(-5, 0),(5, 0)
C.(0,-5),(0, 5) D.(0,-7),(0, 7)
?
B
3.平面内有两个定点F1(-5,0)和F2(5,0),动点P满足|PF1|-|PF2|=6,则动点P的轨迹方程是( )
A. ????216?????29?=1(x≤-4) B. ????29?- ????216?=1(x≤-3)
C. ????216?- ????29?=1(x≥4) D. ????29?- ????216?=1(x≥3)
?
D
4.双曲线的两焦点坐标是F1(0, 3),F2(0,-3),b=2,则双曲线的标准方程是______________.
c = 3
F1(0, 3),F2(0,-3)
b=2
a2=c2-b2=5
????25?- ????24?=1
?
新知探究
认识双曲线
x
y
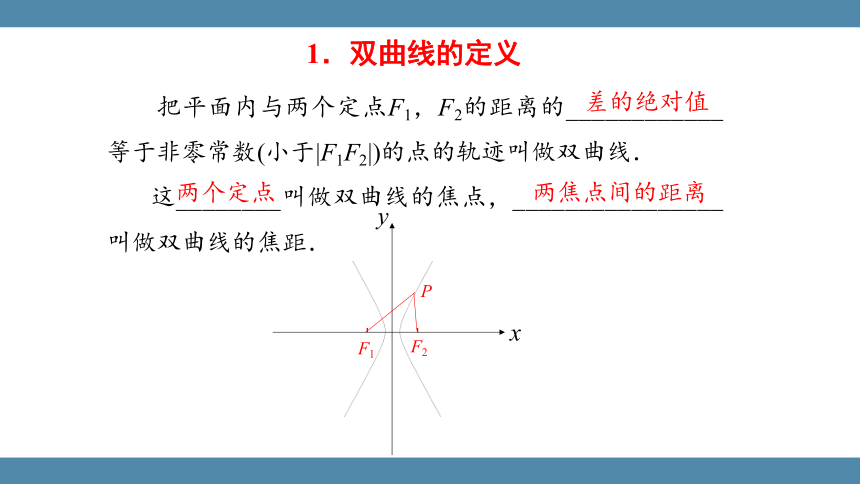
1.双曲线的定义
把平面内与两个定点F1,F2的距离的____________等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这________叫做双曲线的焦点,________________叫做双曲线的焦距.
差的绝对值
两个定点
两焦点间的距离
F1
F2
P
当2a<|F1F2|时,轨迹是双曲线;
当2a=|F1F2|时,轨迹是分别以F1,F2为端点的两条射线;
当2a>|F1F2|时,轨迹不存在.
知识点睛
平面内到两定点F1,F2的距离的差的绝对值为非零常数,即||MF1|-|MF2||=2a,关键词“平面内”.
2.双曲线的标准方程
a2+b2
F1(-c, 0),F2(c, 0)
F1(0,-c),F2(0, c)
(1)标准方程的代数特征
方程右边是1,左边是关于x,y的平方差,并且分母大小关系不确定.
(2)a,b,c三个量的关系
标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里b2=c2-a2,与椭圆中b2=a2-c2相区别,且椭圆中a>b>0,而双曲线中,a,b大小不确定.
知识点睛
题型突破
典例深度剖析 重点多维探究
题型一 双曲线标准方程的认识
[例1] 已知方程????2?????5?????2?????2?=1对应的图形是双曲线,那么k的取值范围是( )
A.k>5 B.k>5或-2 C.k>2或k<-2 D.-2?
[例1] 已知方程????2?????5?????2?????2?=1对应的图形是双曲线,那么k的取值范围是( )
A.k>5 B.k>5或-2 C.k>2或k<-2 D.-2?
解得k>5或-2 ∵方程对应的图形是双曲线,
∴(k-5)(|k|-2)>0.
即
k-5>0
|k|-2>0
或
k-5<0
|k|-2<0
B
方法总结
将双曲线的方程化为标准方程的形式,假如双曲线的方程为????2????+????2?????=1,则当mn<0时,方程表示双曲线.
?
双曲线方程的辨识方法
若 则方程表示焦点在x轴上的双曲线;
m>0
n<0
若 则方程表示焦点在y轴上的双曲线.
m<0
n >0
跟踪训练
1.已知双曲线????2?????3+????22??????=1,焦点在y轴上,若焦距为4,则a等于( )
A. 32 B. 5 C. 7 D. 12
?
焦距为4
c=2
c2=2-a+3-a=4
a= 12
?
焦点在y轴上
D
2.在方程mx2-my2=n中,若mn<0,则方程所表示的曲线是( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的双曲线 D.焦点在y轴上的椭圆
mx2-my2=n
????2?????????????2????????=1
?
mn<0
???????? < 0
?
方程所表示的曲线是焦点在y轴上的双曲线
C
题型二 求双曲线的标准方程
[例2] 求适合下列条件的双曲线的标准方程.
(1)a=3,c=4,焦点在x轴上;
(2)焦点为(0,-6),(0,6),经过点A(-5,6);
(3)以椭圆????28+????25?=1长轴的端点为焦点,且经过点(3,10).
?
[例2] 求适合下列条件的双曲线的标准方程.
(1) a=3,c=4,焦点在x轴上;
由题设知,a=3,c=4,由c2=a2+b2,得b2=c2-a2=42-32=7.
因为双曲线的焦点在x轴上,
所以所求双曲线的标准方程为????29-????27?=1.
?
[例2] 求适合下列条件的双曲线的标准方程.
(2)焦点为(0,-6),(0,6),经过点A(-5,6);
由已知得c=6,且焦点在y轴上.
因为点A(-5,6)在双曲线上,所以
2a=?5?02+6+62??5?02+6?62=|13-5|=8,
则a=4,b2=c2-a2=62-42=20.
所以所求双曲线的标准方程是????216-????220=1.
?
[例2] 求适合下列条件的双曲线的标准方程.
(3)以椭圆????28+????25?=1长轴的端点为焦点,且经过点(3,10).
?
由题意得,双曲线的焦点在x轴上,且c=22.
设双曲线的标准方程为 ????2????2- ????2????2?=1(a>0,b>0),
则有a2+b2=c2=8, 9????2- 10????2?=1,解得a2=3,b2=5.
故所求双曲线的标准方程为????23- ????25?=1.
?
(1)定位:是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
求双曲线标准方程的步骤
(2)定量:是指确定a2,b2的数值,常由条件列方程组求解.
总结归纳
(1)定义法
根据双曲线的定义得到相应的a,b,c,再写出双曲线的标准方程.
[注意] 若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
双曲线标准方程的两种求法
(2)待定系数法
先设出双曲线的标准方程????2????2- ????2????2?=1或????2????2- ????2????2?=1(a,b均为正数),然后根据条件求出待定的系数代入方程即可.
?
方法总结
跟踪训练
3. 根据下列条件,求双曲线的标准方程.
(1)与双曲线????216- ????24?=1有公共焦点,且过点(32,2);
(2)双曲线过两点P(3, 154?),Q(-163, 5).
?
3. 根据下列条件,求双曲线的标准方程.
(1)与双曲线????216- ????24?=1有公共焦点,且过点(32,2);
?
设双曲线的标准方程为????216?????- ????24+?????=1(-4 将点(32?,2)代入,解得k=4或k=-14(舍去),
∴双曲线的标准方程为????212- ????28?=1.
?
3. 根据下列条件,求双曲线的标准方程.
(2)双曲线过两点P(3, 154?),Q(-163, 5).
?
设所求双曲线方程为Ax2+By2=1(AB<0).
∵点(3, 154?), (-163, 5)在双曲线上,
?
∴双曲线的标准方程为????29- ????216=1.
?
解得
∴
9A+22516?B=1
?
2569?A+25B=1
?
A=-116
?
B=19
?
题型三 双曲线定义的应用
[例3] 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|·|PF2|=32.试求△F1PF2的面积.
?
[例3] 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|·|PF2|=32. 试求△F1PF2的面积.
?
因为P是双曲线左支上的点,所以|PF2|-|PF1|=6,
两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,
所以|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.
在△F1PF2中,由余弦定理,
得cos∠F1PF2= ????????12+????????22?????1????222????????1?????????2?= 100?1002????????1?????????2?=0,
所以∠F1PF2=90°,所以S△F1PF2= 12?|PF1|·|PF2|= 12?×32=16.
?
多维探究
变式1 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且其上一点P到焦点F1的距离为10. 求点P到F2的距离.
?
由双曲线的标准方程????29-????216?=1,
得a=3,b=4,c=5.
由双曲线定义得||PF1|-|PF2||=2a=6,
∴|10-|PF2||=6,
解得|PF2|=4或|PF2|=16.
?
变式2 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|:|PF2|=2:5. 试求△F1PF2的面积.
?
由|PF1|∶|PF2|=2∶5,|PF2|-|PF1|=6,
可知|PF2|=10,|PF1|=4,
∴S△F1PF2= 12?×4×46?=86.
?
在解决双曲线中与焦点有关的问题时,要注意定义中的条件||PF1|-|PF2||=2a的应用;
技法点拨
与三角形有关的问题要考虑正、余弦定理、勾股定理等.
另外在运算中要注意一些变形技巧和整体代换思想的应用.
随堂检测
1.双曲线方程为x2-2y2=1,则它的右焦点坐标为( )
A. 22,0? B. 52,0
C. 62,0 D. 3,0
?
C
2.已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2= 60°,则|PF1|·|PF2|等于( )
A.2 B.4 C.6 D.8
在△PF1F2中,
|F1F2|2=|PF1|2+|PF2|2-2|PF1 |·|PF2|·cos 60°
=(|PF1|-|PF2|)2+|PF1|·|PF2|,
即(22)2=22+|PF1|·|PF2|,
解得|PF1|·|PF2|=4.
?
B
3.已知双曲线x2-????22=1的焦点为F1,F2,点M在双曲线上且????????1?????????2?=0,则点M到x轴的距离为( )
A. 43 B. 53
C. 233 D. 3
?
由条件知c=3?,∴|F1F2|=23?,
∵ ????????1?????????2?=0,∴|MO|= 12?|F1F2|=3?,
设M(x0,y0),
?
则点M到x轴的距离为233.
?
则
????02+????02=3
?
????02?-????022=1
?
解得
????02=53
?
????02=43
?
C
4.双曲线8kx2-ky2=8的一个焦点为(0,3),那么k的值是______.
由已知,得????21?????????28????=1.
?
∵焦点为(0,3),∴k<0. ∴ ????2?8?????????2?1?????=1.
∵a2=-8?????,b2=-1?????,c=3,∴-8????+(- 1?????)=9,
∴k=-1.
?
-1
(1)距离的差要加绝对值,否则只为双曲线的一支.若F1,F2表示双曲线的左、右焦点,且点P满足|PF1|-|PF2|=2a,则点P在右支上;若点P满足|PF2|-|PF1|=2a,则点P在左支上.
1.对双曲线定义的两点说明
本课小结
(2)在双曲线定义中,规定2a<|F1F1|,若把|F1F2|用2c表示,则当2a<2c时,P的轨迹为双曲线;当2a=2c时,P的轨迹为以F1,F2为端点的两条射线;当2a>2c时,动点P的轨迹不存在.
本课小结
(1)只有当双曲线的两焦点F1,F2在坐标轴上,并且线段F1F2的垂直平分线也是坐标轴时,得到的方程才是双曲线的标准方程.
(2)标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件、这里b2=c2-a2与椭圆中b2=a2-c2相区别,且椭圆中a>b>0,而双曲线中a,b大小则不确定.
(3)焦点F1,F2的位置,是双曲线定位的条件,它决定了双曲线标准方程的类型.“焦点跟着正项走”.若x2项的系数为正,则焦点在x轴上,若y2项的系数为正,则焦点在y轴上.
(4)双曲线的标准方程都可化为一个统一的形式,即Ax2+By2=1(AB<0).
2.对双曲线标准方程的四点认识
通过本节课,你学会了什么?
1.了解双曲线的定义、几何图形和标准方程的推导过程.
2.掌握双曲线的标准方程.
3.会利用双曲线的定义和标准方程解决简单的应用问题.
本节目标
课前预习
预习课本P118~121,思考并完成以下问题
1.平面内满足什么条件的点的轨迹是双曲线?双曲线的焦点、焦距分别是什么?
2.什么是双曲线的标准方程?
课前小测
(3)双曲线标准方程中,a,b的大小关系是a>b. ( )
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
(2)在双曲线标准方程????2????2?????2????2?=1中,a>0,b>0且a≠b. ( )
?
×
×
×
2.已知双曲线????216?????29?=1,则双曲线的焦点坐标为( )
A.(-7?, 0),(7, 0) B.(-5, 0),(5, 0)
C.(0,-5),(0, 5) D.(0,-7),(0, 7)
?
B
3.平面内有两个定点F1(-5,0)和F2(5,0),动点P满足|PF1|-|PF2|=6,则动点P的轨迹方程是( )
A. ????216?????29?=1(x≤-4) B. ????29?- ????216?=1(x≤-3)
C. ????216?- ????29?=1(x≥4) D. ????29?- ????216?=1(x≥3)
?
D
4.双曲线的两焦点坐标是F1(0, 3),F2(0,-3),b=2,则双曲线的标准方程是______________.
c = 3
F1(0, 3),F2(0,-3)
b=2
a2=c2-b2=5
????25?- ????24?=1
?
新知探究
认识双曲线
x
y
1.双曲线的定义
把平面内与两个定点F1,F2的距离的____________等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这________叫做双曲线的焦点,________________叫做双曲线的焦距.
差的绝对值
两个定点
两焦点间的距离
F1
F2
P
当2a<|F1F2|时,轨迹是双曲线;
当2a=|F1F2|时,轨迹是分别以F1,F2为端点的两条射线;
当2a>|F1F2|时,轨迹不存在.
知识点睛
平面内到两定点F1,F2的距离的差的绝对值为非零常数,即||MF1|-|MF2||=2a,关键词“平面内”.
2.双曲线的标准方程
a2+b2
F1(-c, 0),F2(c, 0)
F1(0,-c),F2(0, c)
(1)标准方程的代数特征
方程右边是1,左边是关于x,y的平方差,并且分母大小关系不确定.
(2)a,b,c三个量的关系
标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里b2=c2-a2,与椭圆中b2=a2-c2相区别,且椭圆中a>b>0,而双曲线中,a,b大小不确定.
知识点睛
题型突破
典例深度剖析 重点多维探究
题型一 双曲线标准方程的认识
[例1] 已知方程????2?????5?????2?????2?=1对应的图形是双曲线,那么k的取值范围是( )
A.k>5 B.k>5或-2
[例1] 已知方程????2?????5?????2?????2?=1对应的图形是双曲线,那么k的取值范围是( )
A.k>5 B.k>5或-2
解得k>5或-2
∴(k-5)(|k|-2)>0.
即
k-5>0
|k|-2>0
或
k-5<0
|k|-2<0
B
方法总结
将双曲线的方程化为标准方程的形式,假如双曲线的方程为????2????+????2?????=1,则当mn<0时,方程表示双曲线.
?
双曲线方程的辨识方法
若 则方程表示焦点在x轴上的双曲线;
m>0
n<0
若 则方程表示焦点在y轴上的双曲线.
m<0
n >0
跟踪训练
1.已知双曲线????2?????3+????22??????=1,焦点在y轴上,若焦距为4,则a等于( )
A. 32 B. 5 C. 7 D. 12
?
焦距为4
c=2
c2=2-a+3-a=4
a= 12
?
焦点在y轴上
D
2.在方程mx2-my2=n中,若mn<0,则方程所表示的曲线是( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的双曲线 D.焦点在y轴上的椭圆
mx2-my2=n
????2?????????????2????????=1
?
mn<0
???????? < 0
?
方程所表示的曲线是焦点在y轴上的双曲线
C
题型二 求双曲线的标准方程
[例2] 求适合下列条件的双曲线的标准方程.
(1)a=3,c=4,焦点在x轴上;
(2)焦点为(0,-6),(0,6),经过点A(-5,6);
(3)以椭圆????28+????25?=1长轴的端点为焦点,且经过点(3,10).
?
[例2] 求适合下列条件的双曲线的标准方程.
(1) a=3,c=4,焦点在x轴上;
由题设知,a=3,c=4,由c2=a2+b2,得b2=c2-a2=42-32=7.
因为双曲线的焦点在x轴上,
所以所求双曲线的标准方程为????29-????27?=1.
?
[例2] 求适合下列条件的双曲线的标准方程.
(2)焦点为(0,-6),(0,6),经过点A(-5,6);
由已知得c=6,且焦点在y轴上.
因为点A(-5,6)在双曲线上,所以
2a=?5?02+6+62??5?02+6?62=|13-5|=8,
则a=4,b2=c2-a2=62-42=20.
所以所求双曲线的标准方程是????216-????220=1.
?
[例2] 求适合下列条件的双曲线的标准方程.
(3)以椭圆????28+????25?=1长轴的端点为焦点,且经过点(3,10).
?
由题意得,双曲线的焦点在x轴上,且c=22.
设双曲线的标准方程为 ????2????2- ????2????2?=1(a>0,b>0),
则有a2+b2=c2=8, 9????2- 10????2?=1,解得a2=3,b2=5.
故所求双曲线的标准方程为????23- ????25?=1.
?
(1)定位:是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
求双曲线标准方程的步骤
(2)定量:是指确定a2,b2的数值,常由条件列方程组求解.
总结归纳
(1)定义法
根据双曲线的定义得到相应的a,b,c,再写出双曲线的标准方程.
[注意] 若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
双曲线标准方程的两种求法
(2)待定系数法
先设出双曲线的标准方程????2????2- ????2????2?=1或????2????2- ????2????2?=1(a,b均为正数),然后根据条件求出待定的系数代入方程即可.
?
方法总结
跟踪训练
3. 根据下列条件,求双曲线的标准方程.
(1)与双曲线????216- ????24?=1有公共焦点,且过点(32,2);
(2)双曲线过两点P(3, 154?),Q(-163, 5).
?
3. 根据下列条件,求双曲线的标准方程.
(1)与双曲线????216- ????24?=1有公共焦点,且过点(32,2);
?
设双曲线的标准方程为????216?????- ????24+?????=1(-4
∴双曲线的标准方程为????212- ????28?=1.
?
3. 根据下列条件,求双曲线的标准方程.
(2)双曲线过两点P(3, 154?),Q(-163, 5).
?
设所求双曲线方程为Ax2+By2=1(AB<0).
∵点(3, 154?), (-163, 5)在双曲线上,
?
∴双曲线的标准方程为????29- ????216=1.
?
解得
∴
9A+22516?B=1
?
2569?A+25B=1
?
A=-116
?
B=19
?
题型三 双曲线定义的应用
[例3] 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|·|PF2|=32.试求△F1PF2的面积.
?
[例3] 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|·|PF2|=32. 试求△F1PF2的面积.
?
因为P是双曲线左支上的点,所以|PF2|-|PF1|=6,
两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,
所以|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.
在△F1PF2中,由余弦定理,
得cos∠F1PF2= ????????12+????????22?????1????222????????1?????????2?= 100?1002????????1?????????2?=0,
所以∠F1PF2=90°,所以S△F1PF2= 12?|PF1|·|PF2|= 12?×32=16.
?
多维探究
变式1 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且其上一点P到焦点F1的距离为10. 求点P到F2的距离.
?
由双曲线的标准方程????29-????216?=1,
得a=3,b=4,c=5.
由双曲线定义得||PF1|-|PF2||=2a=6,
∴|10-|PF2||=6,
解得|PF2|=4或|PF2|=16.
?
变式2 已知F1,F2分别是双曲线????29-????216?=1的左、右焦点,若P是双曲线左支上的点,且|PF1|:|PF2|=2:5. 试求△F1PF2的面积.
?
由|PF1|∶|PF2|=2∶5,|PF2|-|PF1|=6,
可知|PF2|=10,|PF1|=4,
∴S△F1PF2= 12?×4×46?=86.
?
在解决双曲线中与焦点有关的问题时,要注意定义中的条件||PF1|-|PF2||=2a的应用;
技法点拨
与三角形有关的问题要考虑正、余弦定理、勾股定理等.
另外在运算中要注意一些变形技巧和整体代换思想的应用.
随堂检测
1.双曲线方程为x2-2y2=1,则它的右焦点坐标为( )
A. 22,0? B. 52,0
C. 62,0 D. 3,0
?
C
2.已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2= 60°,则|PF1|·|PF2|等于( )
A.2 B.4 C.6 D.8
在△PF1F2中,
|F1F2|2=|PF1|2+|PF2|2-2|PF1 |·|PF2|·cos 60°
=(|PF1|-|PF2|)2+|PF1|·|PF2|,
即(22)2=22+|PF1|·|PF2|,
解得|PF1|·|PF2|=4.
?
B
3.已知双曲线x2-????22=1的焦点为F1,F2,点M在双曲线上且????????1?????????2?=0,则点M到x轴的距离为( )
A. 43 B. 53
C. 233 D. 3
?
由条件知c=3?,∴|F1F2|=23?,
∵ ????????1?????????2?=0,∴|MO|= 12?|F1F2|=3?,
设M(x0,y0),
?
则点M到x轴的距离为233.
?
则
????02+????02=3
?
????02?-????022=1
?
解得
????02=53
?
????02=43
?
C
4.双曲线8kx2-ky2=8的一个焦点为(0,3),那么k的值是______.
由已知,得????21?????????28????=1.
?
∵焦点为(0,3),∴k<0. ∴ ????2?8?????????2?1?????=1.
∵a2=-8?????,b2=-1?????,c=3,∴-8????+(- 1?????)=9,
∴k=-1.
?
-1
(1)距离的差要加绝对值,否则只为双曲线的一支.若F1,F2表示双曲线的左、右焦点,且点P满足|PF1|-|PF2|=2a,则点P在右支上;若点P满足|PF2|-|PF1|=2a,则点P在左支上.
1.对双曲线定义的两点说明
本课小结
(2)在双曲线定义中,规定2a<|F1F1|,若把|F1F2|用2c表示,则当2a<2c时,P的轨迹为双曲线;当2a=2c时,P的轨迹为以F1,F2为端点的两条射线;当2a>2c时,动点P的轨迹不存在.
本课小结
(1)只有当双曲线的两焦点F1,F2在坐标轴上,并且线段F1F2的垂直平分线也是坐标轴时,得到的方程才是双曲线的标准方程.
(2)标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件、这里b2=c2-a2与椭圆中b2=a2-c2相区别,且椭圆中a>b>0,而双曲线中a,b大小则不确定.
(3)焦点F1,F2的位置,是双曲线定位的条件,它决定了双曲线标准方程的类型.“焦点跟着正项走”.若x2项的系数为正,则焦点在x轴上,若y2项的系数为正,则焦点在y轴上.
(4)双曲线的标准方程都可化为一个统一的形式,即Ax2+By2=1(AB<0).
2.对双曲线标准方程的四点认识
通过本节课,你学会了什么?
