人教版(2019)数学选择性必修一 3.2.2双曲线的简单几何性质导学案(有答案)
文档属性
| 名称 | 人教版(2019)数学选择性必修一 3.2.2双曲线的简单几何性质导学案(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 21:16:45 | ||
图片预览



文档简介
3.2.2 双曲线的简单几何性质
【学习目标】
1.掌握双曲线的简单几何性质.
2.了解双曲线的渐近性及渐近线的概念.
3.能区别椭圆与双曲线的性质.
【学习过程】
一、课前预习
预习课本P121~124,思考并完成以下问题
1.双曲线有哪些几何性质?
2.双曲线的顶点、实轴、虚轴分别是什么?
3.双曲线的渐近线、等轴双曲线的定义分别是什么?
二、课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)双曲线-=1的焦点在y轴上. ( )
(2)双曲线的离心率越大,双曲线的开口越开阔. ( )
(3)以y=±2x为渐近线的双曲线有2条. ( )
2.双曲线-y2=1的顶点坐标是( )
A.(4,0),(0,1) B.(-4,0),(4,0)
C.(0,1),(0,-1) D.(-4,0),(0,-1)
3.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( )
A.-=1 B.-=1或-=1
C.-=1 D.-=1或-=1
4.(全国卷Ⅲ)双曲线-=1(a>0)的一条渐近线方程为y=x,则a=________.
三、新知探究
1.双曲线的几何性质
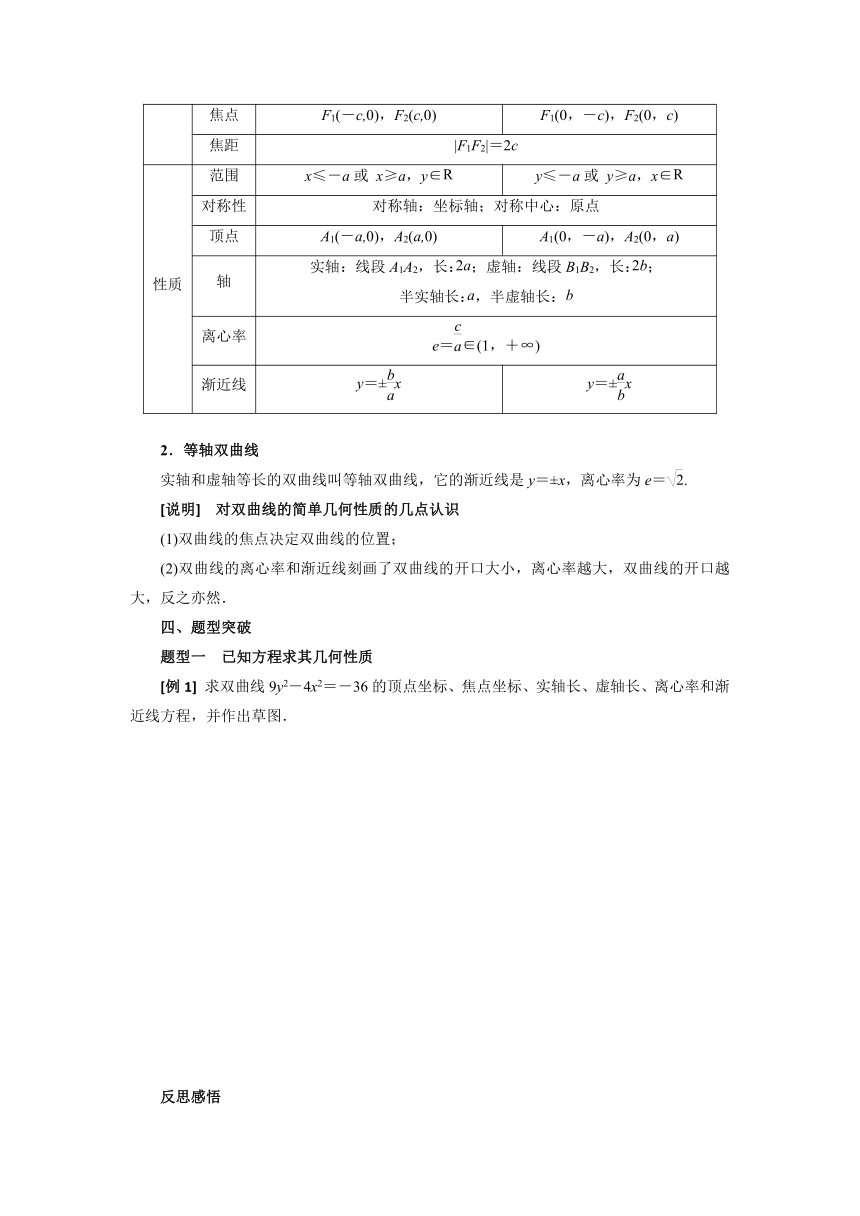
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
性质 图形
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
性质 范围 x≤-a或 x≥a,y∈ y≤-a或 y≥a,x∈
对称性 对称轴:坐标轴;对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:;虚轴:线段B1B2,长:; 半实轴长:,半虚轴长:
离心率 e=∈(1,+∞)
渐近线 y=±x y=±x
2.等轴双曲线
实轴和虚轴等长的双曲线叫等轴双曲线,它的渐近线是y=±x,离心率为e=.
[说明] 对双曲线的简单几何性质的几点认识
(1)双曲线的焦点决定双曲线的位置;
(2)双曲线的离心率和渐近线刻画了双曲线的开口大小,离心率越大,双曲线的开口越大,反之亦然.
四、题型突破
题型一 已知方程求其几何性质
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
反思感悟
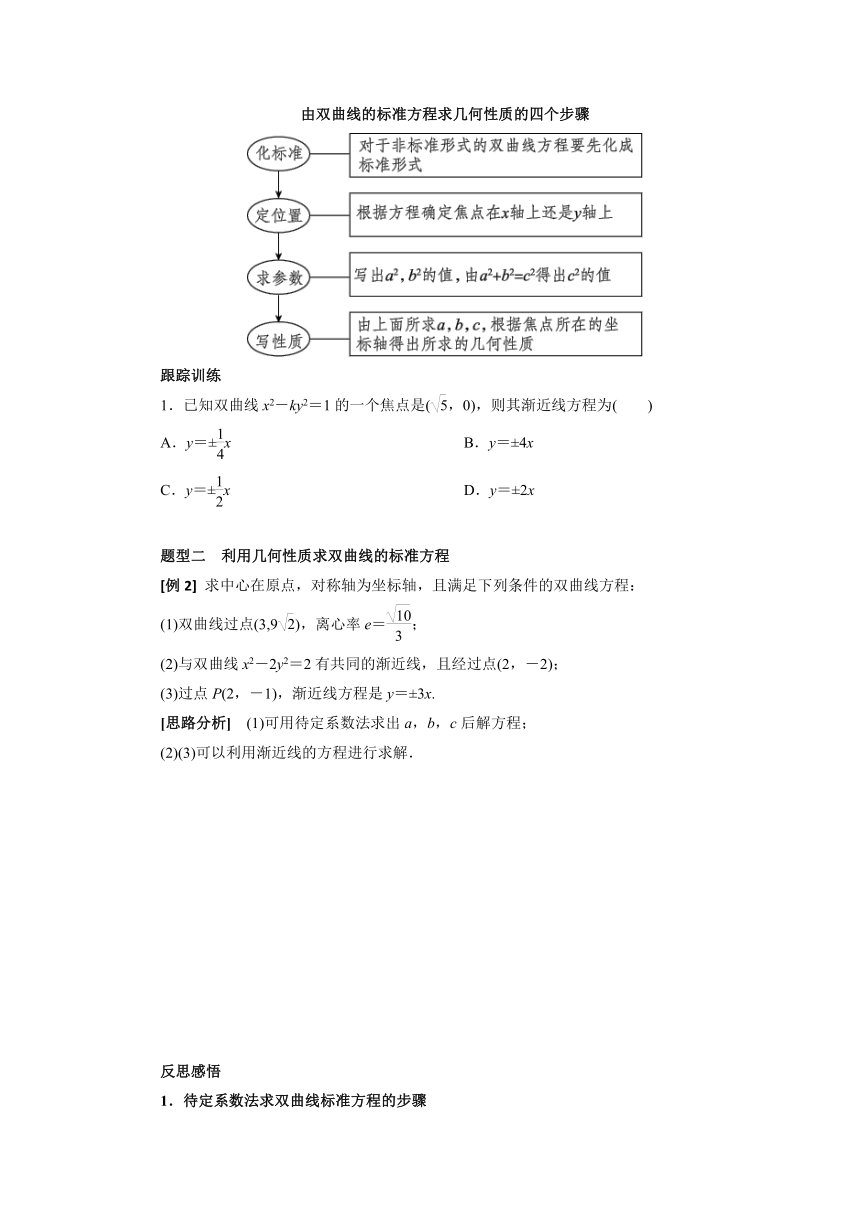
由双曲线的标准方程求几何性质的四个步骤
跟踪训练
1.已知双曲线x2-ky2=1的一个焦点是(,0),则其渐近线方程为( )
A.y=±x B.y=±4x
C.y=±x D.y=±2x
题型二 利用几何性质求双曲线的标准方程
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3,9),离心率e=;
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
(3)过点P(2,-1),渐近线方程是y=±3x.
[思路分析] (1)可用待定系数法求出a,b,c后解方程;
(2)(3)可以利用渐近线的方程进行求解.
反思感悟
1.待定系数法求双曲线标准方程的步骤
2.根据渐近线方程求双曲线方程
(1)若双曲线的渐近线方程为y=±x,则双曲线方程可表示为-=λ(λ≠0).
(2)与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0);与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0).
跟踪训练
2. 双曲线-=1(a>0,b>0)的离心率为2,原点到直线AB的距离为,其中A(0,-b),B(a,0),求该双曲线的标准方程.
题型三 双曲线的离心率、渐近线
[例3] (1)已知双曲线-=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
(2)若F1,F2是双曲线-=1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B.x±3y=0
C.3x±y=0 D.x±3y=0
(3)设F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(+)·=0(O为坐标原点),且||=||,则该双曲线的离心率为________.
反思感悟
1.求双曲线离心率的常见方法
(1)①依据条件求出a,c,利用e=求解;
②利用e=求解;
③依据条件,建立关于a,b,c的齐次关系式,消去b转化为离心率e的方程求解.
(2)求离心率的范围,常结合已知条件构建关于a,b,c的不等关系.
2.求双曲线渐近线方程的两种方法
跟踪训练
3.已知F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为________.
五、达标检测
1.(全国新课标Ⅰ)已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为( )
A.y=±x B.y=±x
C.y=±x D.y=±x
2.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,则C的方程是( )
A.-=1 B.-=1
C.-=1 D.-=1
3.已知0<θ<,则双曲线C1:-=1与C2:-=1的( )
A.实轴长相等 B.虚轴长相等
C.焦距相等 D.离心率相等
4.设F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|+|PF2|=3b,|PF1|·|PF2|=ab,则该双曲线的离心率为( )
A. B. C. D.3
六、本课小结
1.对双曲线的几何性质的四点说明
(1)双曲线的范围反映了其图象是两支,且在范围内向两方无限延伸.
(2)双曲线既是中心对称图形,又是轴对称图形,(0,0)为对称中心,坐标轴为对称轴.
(3)双曲线的离心率e=反映了双曲线开口的大小,e越大,双曲线的开口就越大
(4)双曲线的渐近线是两条直线,当x,y趋向于无穷大时,双曲线将无限地与渐近线接近,但永远没有交点.
2.双曲线与椭圆的六点不同
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实轴、虚轴 长轴、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0a,b,c关系 a2+b2=c2 a2-b2=c2
参考答案
课前小测
1.答案:(1)× (2)√ (3)×
2.答案:B
3.答案:B
4.答案:5
题型突破
[例1] [解析] 将9y2-4x2=-36变形为-=1,
即-=1,∴a=3,b=2,c=,
因此顶点为A1(-3,0),A2(3,0),
焦点坐标为F1(-,0),F2(,0),
实轴长是2a=6,虚轴长是2b=4,
离心率e==,
渐近线方程y=±x.作草图如图所示.
跟踪训练
1.答案:D
解析:双曲线方程化为x2-=1,由题意可得,1+=5,解得k=,即双曲线方程为x2-=1,则其渐近线方程为y=±2x.
[例2] [解析] (1)由e2=,得=,
设a2=9k(k>0),则c2=10k,b2=c2-a2=k.
设所求双曲线方程为-=1①或-=1②.
把(3,9)代入①,得k=-161,与k>0矛盾,无解;
把(3,9)代入②,得k=9.
故所求双曲线方程为-=1.
(2)设所求双曲线方程为x2-2y2=k.③
由于双曲线过点(2,-2),将(2,-2)代入③,
得k=22-2·(-2)2=-4.
故所求双曲线方程为x2-2y2=-4,
即-=1.
(3)由渐近线方程可设所求双曲线方程为-y2=λ(λ≠0).④
将点P(2,-1)代入④,得λ=35,
故所求的双曲线方程为-=1.
跟踪训练
2. 解:∵e=2,
∴1+=4,
∴b2=3a2.①
又∵AB的方程为bx-ay-ab=0,
由点到直线的距离公式,可得=,②
由①②联立,可解得a2=1,b2=3,
∴双曲线方程为x2-=1.
[例3] (1) [答案] A
[解析] 双曲线-=1(a>)的两条渐近线方程为y=±x.由a>,得0<<1,
∴直线y=x的倾斜角小于.
∴=tan=,解得a=.
又c2=a2+2=8,∴c=2,∴e==.
(2)[答案] D
[解析] 由题意得F1(-4,0),F2(4,0),
故双曲线中c=4,
如图所示,若△PF1F2为等腰三角形,
则需满足|PF1|=|F1F2|=8,
依据椭圆与双曲线的定义应有
解得a=3,
故b==,
又双曲线的焦点在x轴上,
故所对应的渐近线方程为y=±x,
化为一般式方程为x±3y=0.
故选D.
(3)[答案] +1
[解析]∵(+)·=0,
∴OB⊥PF2,且B为PF2的中点.
又O是F1F2的中点,∴OB∥PF1,∴PF1⊥PF2.
∵|PF1|-|PF2|=2a,又∵||=||,
∴|PF2|=(+1)a,|PF1|=(+3)a.
∴由|PF1|2+|PF2|2=|F1F2|2,得
(12+6)a2+(4+2)a2=4c2,
∴e2=4+2,∴e=+1.
跟踪训练
3.答案:
解析:如图所示,延长F2A交PF1于点B.
依题意可得|BF1|=|PF1|-|PF2|=2a.又因为点A是BF2的中点,所以|OA|=|BF1|,所以b=a.
所以c=a.所以离心率为.
达标检测
1.答案:C
解析:因为双曲线-=1的焦点在x轴上,所以双曲线的渐近线方程为y=±x.又离心率e====,所以=,所以双曲线的渐近线方程为y=±x,故选C.
2.答案:B
解析:由题意可知c=3,a=2,b===,故双曲线的方程为-=1.
3.答案:D
解析:双曲线C1的离心率e1====,双曲线C2的离心率e2======,所以e1=e2,而双曲线C1的实轴长为2a1=2cos θ,虚轴长为2b1=2sin θ,焦距为2c1=2=2,双曲线C2的实轴长为2a2=2sin θ,虚轴长为2b2=2sin θtan θ,焦距为2c2=2=2=2tan θ,所以A,B,C均不对,故选D.
4.答案:B
解析:依题意得|PF1|-|PF2|=±2a,又|PF1|+|PF2|=3b,(|PF1|+|PF2|)2-(|PF1|-|PF2|)2=9b2-4a2,即有4|PF1|·|PF2|=9b2-4a2,又4|PF1|·|PF2|=9ab,因此有9b2-4a2=9ab,即92--4=0,=0,=,该双曲线的离心率e==,故选B.
【学习目标】
1.掌握双曲线的简单几何性质.
2.了解双曲线的渐近性及渐近线的概念.
3.能区别椭圆与双曲线的性质.
【学习过程】
一、课前预习
预习课本P121~124,思考并完成以下问题
1.双曲线有哪些几何性质?
2.双曲线的顶点、实轴、虚轴分别是什么?
3.双曲线的渐近线、等轴双曲线的定义分别是什么?
二、课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)双曲线-=1的焦点在y轴上. ( )
(2)双曲线的离心率越大,双曲线的开口越开阔. ( )
(3)以y=±2x为渐近线的双曲线有2条. ( )
2.双曲线-y2=1的顶点坐标是( )
A.(4,0),(0,1) B.(-4,0),(4,0)
C.(0,1),(0,-1) D.(-4,0),(0,-1)
3.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( )
A.-=1 B.-=1或-=1
C.-=1 D.-=1或-=1
4.(全国卷Ⅲ)双曲线-=1(a>0)的一条渐近线方程为y=x,则a=________.
三、新知探究
1.双曲线的几何性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
性质 图形
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
性质 范围 x≤-a或 x≥a,y∈ y≤-a或 y≥a,x∈
对称性 对称轴:坐标轴;对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:;虚轴:线段B1B2,长:; 半实轴长:,半虚轴长:
离心率 e=∈(1,+∞)
渐近线 y=±x y=±x
2.等轴双曲线
实轴和虚轴等长的双曲线叫等轴双曲线,它的渐近线是y=±x,离心率为e=.
[说明] 对双曲线的简单几何性质的几点认识
(1)双曲线的焦点决定双曲线的位置;
(2)双曲线的离心率和渐近线刻画了双曲线的开口大小,离心率越大,双曲线的开口越大,反之亦然.
四、题型突破
题型一 已知方程求其几何性质
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
反思感悟
由双曲线的标准方程求几何性质的四个步骤
跟踪训练
1.已知双曲线x2-ky2=1的一个焦点是(,0),则其渐近线方程为( )
A.y=±x B.y=±4x
C.y=±x D.y=±2x
题型二 利用几何性质求双曲线的标准方程
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3,9),离心率e=;
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
(3)过点P(2,-1),渐近线方程是y=±3x.
[思路分析] (1)可用待定系数法求出a,b,c后解方程;
(2)(3)可以利用渐近线的方程进行求解.
反思感悟
1.待定系数法求双曲线标准方程的步骤
2.根据渐近线方程求双曲线方程
(1)若双曲线的渐近线方程为y=±x,则双曲线方程可表示为-=λ(λ≠0).
(2)与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0);与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0).
跟踪训练
2. 双曲线-=1(a>0,b>0)的离心率为2,原点到直线AB的距离为,其中A(0,-b),B(a,0),求该双曲线的标准方程.
题型三 双曲线的离心率、渐近线
[例3] (1)已知双曲线-=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
(2)若F1,F2是双曲线-=1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B.x±3y=0
C.3x±y=0 D.x±3y=0
(3)设F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(+)·=0(O为坐标原点),且||=||,则该双曲线的离心率为________.
反思感悟
1.求双曲线离心率的常见方法
(1)①依据条件求出a,c,利用e=求解;
②利用e=求解;
③依据条件,建立关于a,b,c的齐次关系式,消去b转化为离心率e的方程求解.
(2)求离心率的范围,常结合已知条件构建关于a,b,c的不等关系.
2.求双曲线渐近线方程的两种方法
跟踪训练
3.已知F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为________.
五、达标检测
1.(全国新课标Ⅰ)已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为( )
A.y=±x B.y=±x
C.y=±x D.y=±x
2.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,则C的方程是( )
A.-=1 B.-=1
C.-=1 D.-=1
3.已知0<θ<,则双曲线C1:-=1与C2:-=1的( )
A.实轴长相等 B.虚轴长相等
C.焦距相等 D.离心率相等
4.设F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|+|PF2|=3b,|PF1|·|PF2|=ab,则该双曲线的离心率为( )
A. B. C. D.3
六、本课小结
1.对双曲线的几何性质的四点说明
(1)双曲线的范围反映了其图象是两支,且在范围内向两方无限延伸.
(2)双曲线既是中心对称图形,又是轴对称图形,(0,0)为对称中心,坐标轴为对称轴.
(3)双曲线的离心率e=反映了双曲线开口的大小,e越大,双曲线的开口就越大
(4)双曲线的渐近线是两条直线,当x,y趋向于无穷大时,双曲线将无限地与渐近线接近,但永远没有交点.
2.双曲线与椭圆的六点不同
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实轴、虚轴 长轴、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0
参考答案
课前小测
1.答案:(1)× (2)√ (3)×
2.答案:B
3.答案:B
4.答案:5
题型突破
[例1] [解析] 将9y2-4x2=-36变形为-=1,
即-=1,∴a=3,b=2,c=,
因此顶点为A1(-3,0),A2(3,0),
焦点坐标为F1(-,0),F2(,0),
实轴长是2a=6,虚轴长是2b=4,
离心率e==,
渐近线方程y=±x.作草图如图所示.
跟踪训练
1.答案:D
解析:双曲线方程化为x2-=1,由题意可得,1+=5,解得k=,即双曲线方程为x2-=1,则其渐近线方程为y=±2x.
[例2] [解析] (1)由e2=,得=,
设a2=9k(k>0),则c2=10k,b2=c2-a2=k.
设所求双曲线方程为-=1①或-=1②.
把(3,9)代入①,得k=-161,与k>0矛盾,无解;
把(3,9)代入②,得k=9.
故所求双曲线方程为-=1.
(2)设所求双曲线方程为x2-2y2=k.③
由于双曲线过点(2,-2),将(2,-2)代入③,
得k=22-2·(-2)2=-4.
故所求双曲线方程为x2-2y2=-4,
即-=1.
(3)由渐近线方程可设所求双曲线方程为-y2=λ(λ≠0).④
将点P(2,-1)代入④,得λ=35,
故所求的双曲线方程为-=1.
跟踪训练
2. 解:∵e=2,
∴1+=4,
∴b2=3a2.①
又∵AB的方程为bx-ay-ab=0,
由点到直线的距离公式,可得=,②
由①②联立,可解得a2=1,b2=3,
∴双曲线方程为x2-=1.
[例3] (1) [答案] A
[解析] 双曲线-=1(a>)的两条渐近线方程为y=±x.由a>,得0<<1,
∴直线y=x的倾斜角小于.
∴=tan=,解得a=.
又c2=a2+2=8,∴c=2,∴e==.
(2)[答案] D
[解析] 由题意得F1(-4,0),F2(4,0),
故双曲线中c=4,
如图所示,若△PF1F2为等腰三角形,
则需满足|PF1|=|F1F2|=8,
依据椭圆与双曲线的定义应有
解得a=3,
故b==,
又双曲线的焦点在x轴上,
故所对应的渐近线方程为y=±x,
化为一般式方程为x±3y=0.
故选D.
(3)[答案] +1
[解析]∵(+)·=0,
∴OB⊥PF2,且B为PF2的中点.
又O是F1F2的中点,∴OB∥PF1,∴PF1⊥PF2.
∵|PF1|-|PF2|=2a,又∵||=||,
∴|PF2|=(+1)a,|PF1|=(+3)a.
∴由|PF1|2+|PF2|2=|F1F2|2,得
(12+6)a2+(4+2)a2=4c2,
∴e2=4+2,∴e=+1.
跟踪训练
3.答案:
解析:如图所示,延长F2A交PF1于点B.
依题意可得|BF1|=|PF1|-|PF2|=2a.又因为点A是BF2的中点,所以|OA|=|BF1|,所以b=a.
所以c=a.所以离心率为.
达标检测
1.答案:C
解析:因为双曲线-=1的焦点在x轴上,所以双曲线的渐近线方程为y=±x.又离心率e====,所以=,所以双曲线的渐近线方程为y=±x,故选C.
2.答案:B
解析:由题意可知c=3,a=2,b===,故双曲线的方程为-=1.
3.答案:D
解析:双曲线C1的离心率e1====,双曲线C2的离心率e2======,所以e1=e2,而双曲线C1的实轴长为2a1=2cos θ,虚轴长为2b1=2sin θ,焦距为2c1=2=2,双曲线C2的实轴长为2a2=2sin θ,虚轴长为2b2=2sin θtan θ,焦距为2c2=2=2=2tan θ,所以A,B,C均不对,故选D.
4.答案:B
解析:依题意得|PF1|-|PF2|=±2a,又|PF1|+|PF2|=3b,(|PF1|+|PF2|)2-(|PF1|-|PF2|)2=9b2-4a2,即有4|PF1|·|PF2|=9b2-4a2,又4|PF1|·|PF2|=9ab,因此有9b2-4a2=9ab,即92--4=0,=0,=,该双曲线的离心率e==,故选B.
