苏科版数学八年级上册第6章《一次函数》单元检测卷(含答案)
文档属性
| 名称 | 苏科版数学八年级上册第6章《一次函数》单元检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 11:19:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第6章《一次函数》单元检测卷
(时间:90分钟 满分:100分)
一、选择题(每小题2分,共20分)
1.下列式子中,能表示y是X的函数关系的是 ( )
A.y2=x B.x2=y C.=x D.4y2=x
2.伟伟从学校匀速回家,刚到家发现当晚要完成的试卷落在学校了,于是马上以更快的速度匀速原路返回学校,这一情景中,速度v和时间t的函数图像(不考虑图像端点情况)大致是 ( )
3.直线y=-x+2和直线y=x-2的交点P的坐标是 ( )
A.(2,0) B.(-2,0) C.(0,2) D.(0,-2)
4.无论实数m取什么值,直线y=x+m与y=-x+5的交点都不可能在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知一次函数y=(m-1)x+1的图像上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1A.m>0 B.m<0 C.m>1 D.m<1
6.若点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是 ( )
A.6或-6 B.6 C.-6 D.6或3
7.一次函数y=kx+b与y=kbx在同一坐标系内的图像可能为 ( )
8.如图,一次函数y=kx+b的图像经过A,B两点,则kx+b>0的解集是 ( )
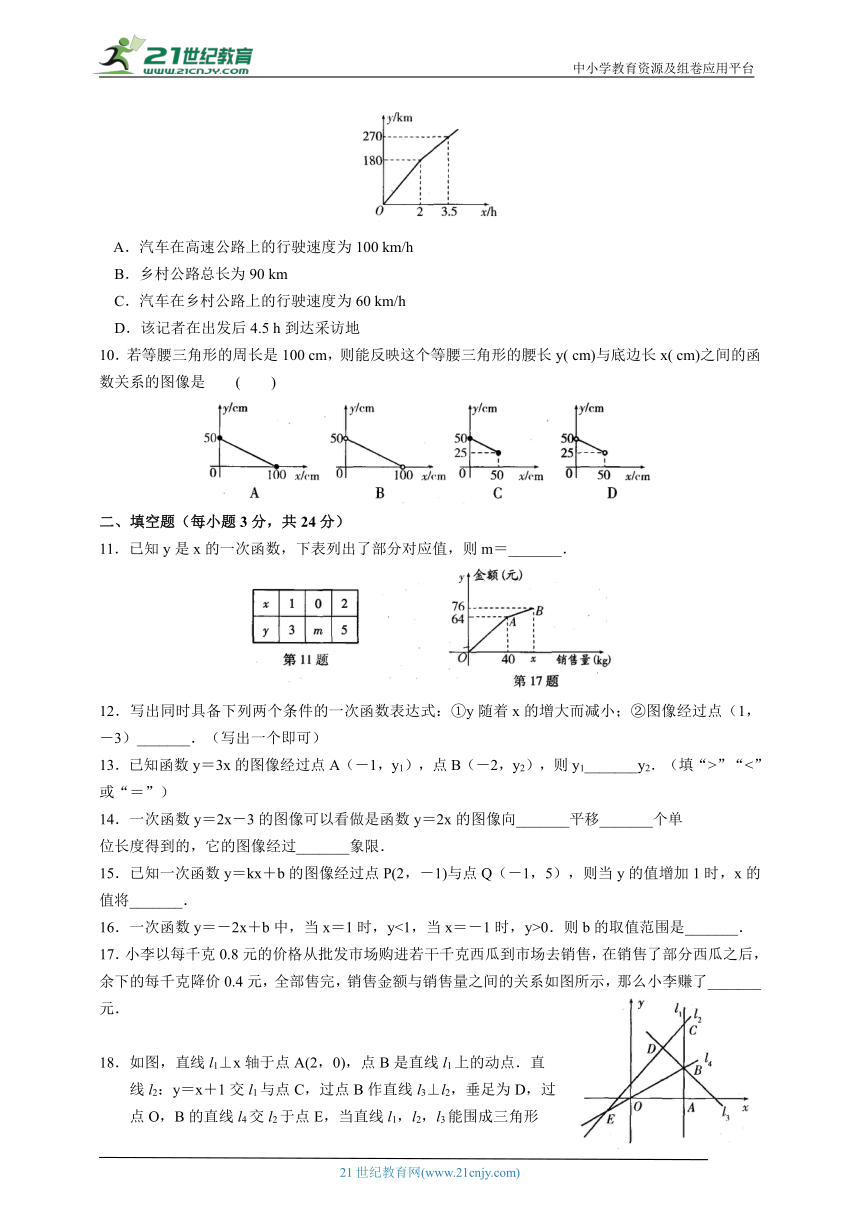
A.x>0 B.x>-3 C.x>2 D.-39.某电视台“走基层”栏目的一位记者乘汽车赴360 km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速
行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是 ( )
A.汽车在高速公路上的行驶速度为100 km/h
B.乡村公路总长为90 km
C.汽车在乡村公路上的行驶速度为60 km/h
D.该记者在出发后4.5 h到达采访地
10.若等腰三角形的周长是100 cm,则能反映这个等腰三角形的腰长y( cm)与底边长x( cm)之间的函数关系的图像是 ( )
二、填空题(每小题3分,共24分)
11.已知y是x的一次函数,下表列出了部分对应值,则m=_______.
12.写出同时具备下列两个条件的一次函数表达式:①y随着x的增大而减小;②图像经过点(1,-3)_______.(写出一个即可)
13.已知函数y=3x的图像经过点A(-1,y1),点B(-2,y2),则y1_______y2.(填“>”“<”或“=”)
14.一次函数y=2x-3的图像可以看做是函数y=2x的图像向_______平移_______个单
位长度得到的,它的图像经过_______象限.
15.已知一次函数y=kx+b的图像经过点P(2,-1)与点Q(-1,5),则当y的值增加1时,x的值将_______.
16.一次函数y=-2x+b中,当x=1时,y<1,当x=-1时,y>0.则b的取值范围是_______.
17.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与销售量之间的关系如图所示,那么小李赚了_______元.
18.如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直
线l2:y=x+1交l1与点C,过点B作直线l3⊥l2,垂足为D,过
点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形
时,设该三角形的面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形的面积为S2.
(1)若点B在线段AC上,且S1=S2,则点B的坐标为_______;
(2)点B在直线l1,且S2=S1,则∠BOA的度数为_______.
三、解答题(共56分)
19.(6分)已知一次函数y=(2m+4)x+(3-n).
(1)当m,n是什么数时,y随x的增大而增大?
(2)当m,n是什么数时,函数图像经过原点?
(3)若图像经过一、二、三象限,求m,n的取值范围.
20.(6分)作出函数y=x-4的图像,并根据图像回答问题:
(1)当x取何值时,y>0
(2)当-1≤x≤2时,求y的取值范围.
21.(8分)某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5 m3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1 m3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元.
(1)求y与x的函数关系式;(纯利润=总收入-总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.
22.(8分)国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区.现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
23.(8分)一报刊销售亭从报社订购某晚报的价格是每份0.7元,销售价是每份1元,卖不掉的报纸还可以以0.20元的价格返回报社,在一个月内(以30天计算),有20天每天可卖出100份,其余10天,每天可卖出60份,但每天报亭从报社订购的份数必须相同,若以报亭每天从报社订购报纸的份数为x,每月所获得的利润为y.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围;
(2)报亭应该每天从报社订购多少份报纸,才能使每月获得的利润最大?最大利润是多少?
24.(10分)小强和爸爸上山游玩,两人距地面的高度y(m)与小强登山时间x(min)之间的函数图像分别如图中折线OAC(小强)和线段DE(爸爸)所示,根据函数图像进行以下探究:
信息读取(1)爸爸登山的速度是每分钟_______m;
(2)请解释图中点B的实际意义;
图像理解(3)求线段DE所表示的y与x之间的函数关
系式,并写出自变量x的取值范围;
(4)m=_______;
问题解决(5)若小强提速后,他登山的速度是爸爸速度的3倍,问:小强登山多长时间时开始提速?此时小强距地面的高度是多少米?
25.(10分)在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
参考答案
1.B 2.A 3.A 4.C 5.D 6.B 7.A 8.B 9.C 10.D 11.1 12.y=-3x 13.> 14.下 3 一、三、四 15.减小 16.-218.(1)(2,0) (2)15°或75°
19.(1) m>-2,n为任何实数.(2) (3)
20.图略.(1)当x>8时,y>0.(2)当-1≤x≤2时,-≤y≤-3.
21.(1)y=19x-8000.(2)x=6000.
22.(1)大货车用8辆,小货车用10辆.(2)w=70a+11 550(0≤a≤8且为整数).(3)11900(元).
23.(1)y=x+480(60≤x≤100且x为整数).(2)当x=100时,y最大值=580(元).
24.(1)10:(2)图中点B的实际意义是:距地面高度为165m时两人相遇(或小强追上爸爸);
(3) y=10x+100(0≤x≤20).(4)6.5.(5)登山2 min时小强开始提速,此时小强距地面的高度是30 m.
25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第6章《一次函数》单元检测卷
(时间:90分钟 满分:100分)
一、选择题(每小题2分,共20分)
1.下列式子中,能表示y是X的函数关系的是 ( )
A.y2=x B.x2=y C.=x D.4y2=x
2.伟伟从学校匀速回家,刚到家发现当晚要完成的试卷落在学校了,于是马上以更快的速度匀速原路返回学校,这一情景中,速度v和时间t的函数图像(不考虑图像端点情况)大致是 ( )
3.直线y=-x+2和直线y=x-2的交点P的坐标是 ( )
A.(2,0) B.(-2,0) C.(0,2) D.(0,-2)
4.无论实数m取什么值,直线y=x+m与y=-x+5的交点都不可能在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知一次函数y=(m-1)x+1的图像上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1
6.若点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是 ( )
A.6或-6 B.6 C.-6 D.6或3
7.一次函数y=kx+b与y=kbx在同一坐标系内的图像可能为 ( )
8.如图,一次函数y=kx+b的图像经过A,B两点,则kx+b>0的解集是 ( )
A.x>0 B.x>-3 C.x>2 D.-3
行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是 ( )
A.汽车在高速公路上的行驶速度为100 km/h
B.乡村公路总长为90 km
C.汽车在乡村公路上的行驶速度为60 km/h
D.该记者在出发后4.5 h到达采访地
10.若等腰三角形的周长是100 cm,则能反映这个等腰三角形的腰长y( cm)与底边长x( cm)之间的函数关系的图像是 ( )
二、填空题(每小题3分,共24分)
11.已知y是x的一次函数,下表列出了部分对应值,则m=_______.
12.写出同时具备下列两个条件的一次函数表达式:①y随着x的增大而减小;②图像经过点(1,-3)_______.(写出一个即可)
13.已知函数y=3x的图像经过点A(-1,y1),点B(-2,y2),则y1_______y2.(填“>”“<”或“=”)
14.一次函数y=2x-3的图像可以看做是函数y=2x的图像向_______平移_______个单
位长度得到的,它的图像经过_______象限.
15.已知一次函数y=kx+b的图像经过点P(2,-1)与点Q(-1,5),则当y的值增加1时,x的值将_______.
16.一次函数y=-2x+b中,当x=1时,y<1,当x=-1时,y>0.则b的取值范围是_______.
17.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与销售量之间的关系如图所示,那么小李赚了_______元.
18.如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直
线l2:y=x+1交l1与点C,过点B作直线l3⊥l2,垂足为D,过
点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形
时,设该三角形的面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形的面积为S2.
(1)若点B在线段AC上,且S1=S2,则点B的坐标为_______;
(2)点B在直线l1,且S2=S1,则∠BOA的度数为_______.
三、解答题(共56分)
19.(6分)已知一次函数y=(2m+4)x+(3-n).
(1)当m,n是什么数时,y随x的增大而增大?
(2)当m,n是什么数时,函数图像经过原点?
(3)若图像经过一、二、三象限,求m,n的取值范围.
20.(6分)作出函数y=x-4的图像,并根据图像回答问题:
(1)当x取何值时,y>0
(2)当-1≤x≤2时,求y的取值范围.
21.(8分)某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5 m3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1 m3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元.
(1)求y与x的函数关系式;(纯利润=总收入-总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.
22.(8分)国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区.现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
23.(8分)一报刊销售亭从报社订购某晚报的价格是每份0.7元,销售价是每份1元,卖不掉的报纸还可以以0.20元的价格返回报社,在一个月内(以30天计算),有20天每天可卖出100份,其余10天,每天可卖出60份,但每天报亭从报社订购的份数必须相同,若以报亭每天从报社订购报纸的份数为x,每月所获得的利润为y.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围;
(2)报亭应该每天从报社订购多少份报纸,才能使每月获得的利润最大?最大利润是多少?
24.(10分)小强和爸爸上山游玩,两人距地面的高度y(m)与小强登山时间x(min)之间的函数图像分别如图中折线OAC(小强)和线段DE(爸爸)所示,根据函数图像进行以下探究:
信息读取(1)爸爸登山的速度是每分钟_______m;
(2)请解释图中点B的实际意义;
图像理解(3)求线段DE所表示的y与x之间的函数关
系式,并写出自变量x的取值范围;
(4)m=_______;
问题解决(5)若小强提速后,他登山的速度是爸爸速度的3倍,问:小强登山多长时间时开始提速?此时小强距地面的高度是多少米?
25.(10分)在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
参考答案
1.B 2.A 3.A 4.C 5.D 6.B 7.A 8.B 9.C 10.D 11.1 12.y=-3x 13.> 14.下 3 一、三、四 15.减小 16.-2
19.(1) m>-2,n为任何实数.(2) (3)
20.图略.(1)当x>8时,y>0.(2)当-1≤x≤2时,-≤y≤-3.
21.(1)y=19x-8000.(2)x=6000.
22.(1)大货车用8辆,小货车用10辆.(2)w=70a+11 550(0≤a≤8且为整数).(3)11900(元).
23.(1)y=x+480(60≤x≤100且x为整数).(2)当x=100时,y最大值=580(元).
24.(1)10:(2)图中点B的实际意义是:距地面高度为165m时两人相遇(或小强追上爸爸);
(3) y=10x+100(0≤x≤20).(4)6.5.(5)登山2 min时小强开始提速,此时小强距地面的高度是30 m.
25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
