人教版(2019)数学选择性必修二 4_1数列的概念 课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 4_1数列的概念 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 07:31:07 | ||
图片预览











文档简介
(共34张PPT)
数列的概念
新课程标准 考向预测 通过实例,了解数列的概念和几种简单的表示方法(列表、图象、通项公式),了解数列是一种特殊函数. 命题角度 1.由an与Sn的关系求an
2.由数列的递推关系求通项公式
3.数列的性质及应用
核心素养 逻辑推理、数学运算
基础梳理
一、数列的概念
含义
数列 按照______________排列的一列数
数列的项 数列中的__________
通项公式 数列{an}的第n项an与n之间的关系能用公式an=f(n)表示,这个公式叫做数列的通项公式
前n项和 数列{an}中,Sn=________________叫做数列的前n项和
一定顺序
每一个数
a1+a2+…+an
知识拓展
若数列{an}的前n项和为Sn,
则an=
1.(2019重庆第一中学月考)已知数列1,, , ,…, ,…,则5是它的( )
A.第62项 B.第63项 C.第64项 D.第68项
B
基础小测
2.若数列{an}的前n项和Sn=n2+1,则an=_______________.
列表法 列表格表示n与an的对应关系
图象法 把点___________画在平面直角坐标系中
公式法 通项公式 把数列的通项使用__________表示的方法
递推公式 使用初始值a1和an+1=f(an)或a1,a2和an+1=f(an,an-1)等表示数列的方法
(n,an)
公式
二、数列的表示方法
通项公式和递推公式的异同点 不同点 相同点
通项公式 可根据某项的序号n的值,直接代入求出an 都可确定一个数列,也都可求出数列的任意一项
递推公式 可根据第一项(或前几项)的值,通过一次(或多次)赋值,逐项求出数列的项,直至求出所需的an 1.(2020届山东济宁邹城高三上学期期中)数列1,-,,-,,…的一个通项公式an=( )
A. B.- C. D.
C
基础小测
2.在数列{an}中,a1=1,an=1+ (n≥2),则a4=________.
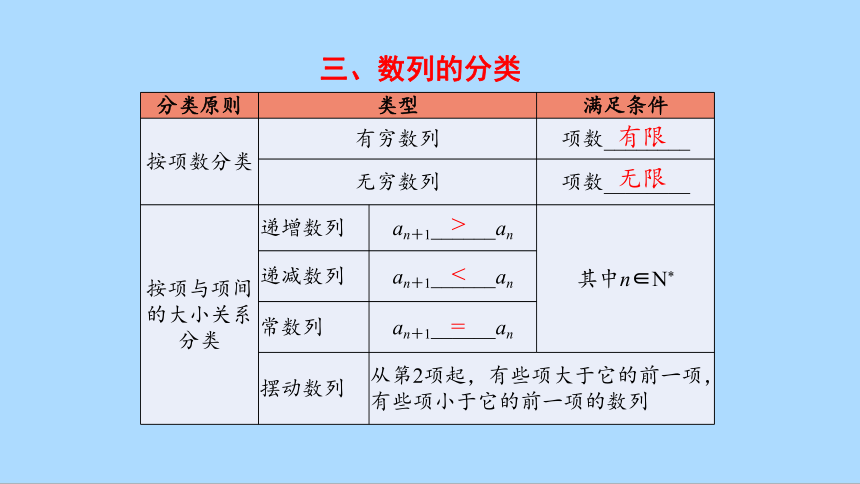
分类原则 类型 满足条件
按项数分类 有穷数列 项数________
无穷数列 项数________
按项与项间的大小关系分类 递增数列 an+1______an 其中n∈N*
递减数列 an+1______an 常数列 an+1______an 摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列 三、数列的分类
有限
无限
>
<
=
下列数列中,既是递增数列又是无穷数列的是( )
A.1, , ,,…
B.-1,-2,-3,-4,…
C.-1,-,- ,- ,…
D.1, , ,…,
C
基础小测
考点突破
考点一 由 an与Sn的关系求通项公式 (高考热度:★★★)
[例1]已知Sn为数列{an}的前n项和,且log2(Sn+1)=n+1,则数列{an}的通项公式为( )
A.an=2n B.an=
C.an=2n-1 D.an=2n+1
B
先利用a1=S1求出a1.
用n-1替换Sn中的n得到一个新的关系式,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的表达式.
对n=1时的结果进行检验,看是否符合n≥2时an的表达式.若符合,则可以把数列的通项公式合写;若不符合,则应该分n=1与n≥2两段来写.
解题技法
已知Sn求an的三个步骤
根据所求结果的不同要求,将问题向不同的两个方向转化.
(1)利用an=Sn-Sn-1(n≥2)转化为只含Sn,Sn-1的关系式,再求解.
(2)利用Sn-Sn-1=an(n≥2)转化为只含an,an-1的关系式,再求解.
解题策略
Sn与an关系问题的求解思路
15
考点微练
(2020届云南师范大学附属中学高三上学期第一次月考)记Sn为数列{an}的前n项和,若满足a1=1,Sn+1=an+1,则S4=________.
已知数列{an}的前n项和Sn满足Sn+an=2n(n∈N*),则a7=( )
A. B.
C. D.
B
对点变式
[例2] (2019湖南师大附中高三月考)已知数列{an}满足a1=,an+1=an+(n∈N*),则a2 019=( )
A.1- B.1-
C.- D. -
C
考点二 由递推关系求数列的通项公式(高考热度:★★)
若数列{an}满足a1= ,an+1=an+ ,则an=________.
对点变式
[例3]设数列{an}的前n项和为Sn,已知a1=1,Sn=4-an(n∈N*),则a2=________,数列{an}的通项公式是an=________.
1
递推关系式可转化为an+1=an+f(n)的数列,通常采用累加法(逐差相加法)求其通项公式.
递推关系式可转化为=f(n)的数列,且容易求数列{f(n)}前n项的积时,采用累乘法求通项公式.
对于递推关系式形如an+1=pan+q(p≠0,1,q≠0)的数列,采用构造法求数列的通项.
由递推关系式求数列通项公式的常用方法
解题技法
一是在连乘的式子中只写到,漏掉a1而导致错误;二是根据连乘求出an之后,不注意检验a1是否成立.
易错提醒
利用构造法求解时应注意数列的首项的正确求解以及准确确定最后一个式子的形式.
利用累乘法,易出现两个方面的问题
1.(2019湖北武汉5月份模拟)数列{an}中,an+1=2an+1,a1=1,则a6=( )
A.32 B.62
C.63 D.64
C
考点微练
2.设数列{an}的前n项和为Sn,且a1=1,{Sn+nan}为常数列,则an=( )
A. B.
C. D.
B
考点三 数列的函数特性(高考热度:★)
考向1 数列的周期性
[例4] 在数列{an}中,a1=0,an+1=,则S2020=____.
0
先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值.
解决数列周期性问题的方法
技法
点拨
考向2 数列的单调性
[例5] 已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}(n≥7,n∈N*)为递增数列,则实数λ的取值范围为____________.
(-16,+∞)
解决数列的单调性问题的3种方法
作差比较法 根据an+1-an的符号判断数列{an}是递增数列、递减数列或是常数列
作商比较法 根据(an>0或an<0)与1的大小关系进行判断
数形结合法 结合相应函数的图象直观判断
方法总结
考向3 数列的最大(小)项
[例6] 数列{an}的通项an=,则数列{an}中的最大项是( )
A.3 B.19
C. D.
C
(1)将数列视为函数f(x)当x∈N*时所对应的一列函数值,根据f(x)的类型作出相应的函数图象,或利用求函数最值的方法,求出f(x)的最值,进而求出数列的最大(小)项.
(2)通过通项公式an研究数列的单调性,利用
(n≥2)确定最大项,利用(n≥2)确定最小项.
求数列的最大项与最小项的常用方法
方法总结
(3)比较法:
若有an+1-an=f(n+1)-f(n)>0(或an>0时,>1),则an+1>an,则数列{an}是递增数列,所以数列{an}的最小项为a1=f(1);若有an+1-an=f(n+1)-f(n)<0 (或an>0时,<1) ,则an+1<an,则数列{an}是递减数列,所以数列{an}的最大项为a1=f(1).
方法总结
考点微练
1.已知数列{an}的通项公式为an= .若数列{an}为递减数列,则实数k的取值范围是( )
A.(3,+∞) B.(2,+∞)
C.(1,+∞) D.(0,+∞)
D
2.(多选题)已知数列{an}的通项为an= ,则下列表述正确的是( )
A.数列{an}的最大项为0
B.数列{an}的最大项不存在
C.数列{an}的最小项为-
D.数列{an}的最小项为-
AD
解析过程见配套学案
通过本节课,你学会了什么?
数列的概念
新课程标准 考向预测 通过实例,了解数列的概念和几种简单的表示方法(列表、图象、通项公式),了解数列是一种特殊函数. 命题角度 1.由an与Sn的关系求an
2.由数列的递推关系求通项公式
3.数列的性质及应用
核心素养 逻辑推理、数学运算
基础梳理
一、数列的概念
含义
数列 按照______________排列的一列数
数列的项 数列中的__________
通项公式 数列{an}的第n项an与n之间的关系能用公式an=f(n)表示,这个公式叫做数列的通项公式
前n项和 数列{an}中,Sn=________________叫做数列的前n项和
一定顺序
每一个数
a1+a2+…+an
知识拓展
若数列{an}的前n项和为Sn,
则an=
1.(2019重庆第一中学月考)已知数列1,, , ,…, ,…,则5是它的( )
A.第62项 B.第63项 C.第64项 D.第68项
B
基础小测
2.若数列{an}的前n项和Sn=n2+1,则an=_______________.
列表法 列表格表示n与an的对应关系
图象法 把点___________画在平面直角坐标系中
公式法 通项公式 把数列的通项使用__________表示的方法
递推公式 使用初始值a1和an+1=f(an)或a1,a2和an+1=f(an,an-1)等表示数列的方法
(n,an)
公式
二、数列的表示方法
通项公式和递推公式的异同点 不同点 相同点
通项公式 可根据某项的序号n的值,直接代入求出an 都可确定一个数列,也都可求出数列的任意一项
递推公式 可根据第一项(或前几项)的值,通过一次(或多次)赋值,逐项求出数列的项,直至求出所需的an 1.(2020届山东济宁邹城高三上学期期中)数列1,-,,-,,…的一个通项公式an=( )
A. B.- C. D.
C
基础小测
2.在数列{an}中,a1=1,an=1+ (n≥2),则a4=________.
分类原则 类型 满足条件
按项数分类 有穷数列 项数________
无穷数列 项数________
按项与项间的大小关系分类 递增数列 an+1______an 其中n∈N*
递减数列 an+1______an 常数列 an+1______an 摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列 三、数列的分类
有限
无限
>
<
=
下列数列中,既是递增数列又是无穷数列的是( )
A.1, , ,,…
B.-1,-2,-3,-4,…
C.-1,-,- ,- ,…
D.1, , ,…,
C
基础小测
考点突破
考点一 由 an与Sn的关系求通项公式 (高考热度:★★★)
[例1]已知Sn为数列{an}的前n项和,且log2(Sn+1)=n+1,则数列{an}的通项公式为( )
A.an=2n B.an=
C.an=2n-1 D.an=2n+1
B
先利用a1=S1求出a1.
用n-1替换Sn中的n得到一个新的关系式,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的表达式.
对n=1时的结果进行检验,看是否符合n≥2时an的表达式.若符合,则可以把数列的通项公式合写;若不符合,则应该分n=1与n≥2两段来写.
解题技法
已知Sn求an的三个步骤
根据所求结果的不同要求,将问题向不同的两个方向转化.
(1)利用an=Sn-Sn-1(n≥2)转化为只含Sn,Sn-1的关系式,再求解.
(2)利用Sn-Sn-1=an(n≥2)转化为只含an,an-1的关系式,再求解.
解题策略
Sn与an关系问题的求解思路
15
考点微练
(2020届云南师范大学附属中学高三上学期第一次月考)记Sn为数列{an}的前n项和,若满足a1=1,Sn+1=an+1,则S4=________.
已知数列{an}的前n项和Sn满足Sn+an=2n(n∈N*),则a7=( )
A. B.
C. D.
B
对点变式
[例2] (2019湖南师大附中高三月考)已知数列{an}满足a1=,an+1=an+(n∈N*),则a2 019=( )
A.1- B.1-
C.- D. -
C
考点二 由递推关系求数列的通项公式(高考热度:★★)
若数列{an}满足a1= ,an+1=an+ ,则an=________.
对点变式
[例3]设数列{an}的前n项和为Sn,已知a1=1,Sn=4-an(n∈N*),则a2=________,数列{an}的通项公式是an=________.
1
递推关系式可转化为an+1=an+f(n)的数列,通常采用累加法(逐差相加法)求其通项公式.
递推关系式可转化为=f(n)的数列,且容易求数列{f(n)}前n项的积时,采用累乘法求通项公式.
对于递推关系式形如an+1=pan+q(p≠0,1,q≠0)的数列,采用构造法求数列的通项.
由递推关系式求数列通项公式的常用方法
解题技法
一是在连乘的式子中只写到,漏掉a1而导致错误;二是根据连乘求出an之后,不注意检验a1是否成立.
易错提醒
利用构造法求解时应注意数列的首项的正确求解以及准确确定最后一个式子的形式.
利用累乘法,易出现两个方面的问题
1.(2019湖北武汉5月份模拟)数列{an}中,an+1=2an+1,a1=1,则a6=( )
A.32 B.62
C.63 D.64
C
考点微练
2.设数列{an}的前n项和为Sn,且a1=1,{Sn+nan}为常数列,则an=( )
A. B.
C. D.
B
考点三 数列的函数特性(高考热度:★)
考向1 数列的周期性
[例4] 在数列{an}中,a1=0,an+1=,则S2020=____.
0
先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值.
解决数列周期性问题的方法
技法
点拨
考向2 数列的单调性
[例5] 已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}(n≥7,n∈N*)为递增数列,则实数λ的取值范围为____________.
(-16,+∞)
解决数列的单调性问题的3种方法
作差比较法 根据an+1-an的符号判断数列{an}是递增数列、递减数列或是常数列
作商比较法 根据(an>0或an<0)与1的大小关系进行判断
数形结合法 结合相应函数的图象直观判断
方法总结
考向3 数列的最大(小)项
[例6] 数列{an}的通项an=,则数列{an}中的最大项是( )
A.3 B.19
C. D.
C
(1)将数列视为函数f(x)当x∈N*时所对应的一列函数值,根据f(x)的类型作出相应的函数图象,或利用求函数最值的方法,求出f(x)的最值,进而求出数列的最大(小)项.
(2)通过通项公式an研究数列的单调性,利用
(n≥2)确定最大项,利用(n≥2)确定最小项.
求数列的最大项与最小项的常用方法
方法总结
(3)比较法:
若有an+1-an=f(n+1)-f(n)>0(或an>0时,>1),则an+1>an,则数列{an}是递增数列,所以数列{an}的最小项为a1=f(1);若有an+1-an=f(n+1)-f(n)<0 (或an>0时,<1) ,则an+1<an,则数列{an}是递减数列,所以数列{an}的最大项为a1=f(1).
方法总结
考点微练
1.已知数列{an}的通项公式为an= .若数列{an}为递减数列,则实数k的取值范围是( )
A.(3,+∞) B.(2,+∞)
C.(1,+∞) D.(0,+∞)
D
2.(多选题)已知数列{an}的通项为an= ,则下列表述正确的是( )
A.数列{an}的最大项为0
B.数列{an}的最大项不存在
C.数列{an}的最小项为-
D.数列{an}的最小项为-
AD
解析过程见配套学案
通过本节课,你学会了什么?
