人教版(2019)数学选择性必修二 4_2等差数列 课件(共35张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 4_2等差数列 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 727.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 07:32:58 | ||
图片预览











文档简介
(共35张PPT)
等差数列
新课程标准 考向预测 1.通过实例,理解等差数列的概念. 2.探索并掌握等差数列的通项公式与前n项和的公式. 3.能在具体的问题情境中,发现数列的等差关系,并能用有关知识解决相应的问题. 4.体会等差数列与一次函数的关系. 命题角度 1.等差数列的基本运算
2.等差数列的判定与证明
3.等差数列的性质及应用
核心素养 逻辑推理、数学运算
基础梳理
一、等差数列的有关概念
如果一个数列从第2项起,每一项与它的前一项的差都等于____________,那么这个数列就叫做等差数列.这个常数叫做等差数列的_______,符号表示为_______________(n∈N*,d为常数).
定义
同一个常数
公差
an+1-an=d
要注意概念中的 “从第2项起”.如果一个数列不是从第2项起,而是从第3项或第4项起,每一项与它的前一项的差是同一个常数,那么此数列不是等差数列.
易错提示
若等差数列{an}的首项是a1,公差是d,则其通项公式为an=____________.
如果a,A,b成等差数列,那么A叫做a,b的等差中项,且A=__________.
等差中项
通项公式
a1+(n-1)d
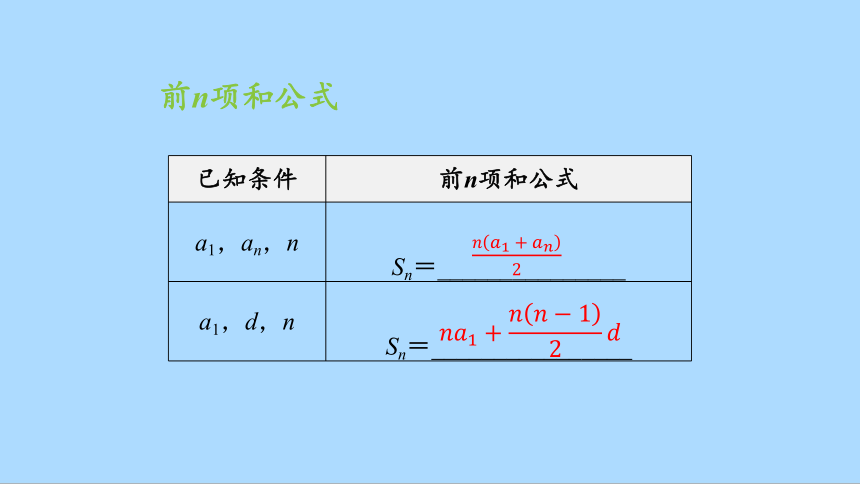
前n项和公式
已知条件 前n项和公式
a1,an,n Sn=_______________
a1,d,n Sn=________________
C
基础小测
1.在等差数列11,8,5,…中,-49是它的( )
A.第19项 B.第20项
C.第21项 D.第22项
2.(2020届四川天府名校上学期第一轮联合质量测评)已知数列{an}满an+2-an+1=an+1-an(n∈N*),且a5=10,a7=14,则a2020-a2019=( )
A.2 B.1
C.-2 D.-1
A
1.等差数列的通项公式an=a1+(n-1)d,是关于n的一次函数.对应结论:(1)an=am+(n-m)d;(2)an=nd+(a1-d);(3)d= (n≠1)或d= (m≠n).
知识拓展
2.等差数列的前n项和公式Sn= =na1+,前一个公式(由倒序相加法推得)与中项有关(相当于n个等差中项之和),后一个公式是关于n的没有常数项的二次函数(Sn=An2+Bn).
二、等差数列的有关性质
类型 性质
项的性质 k+l=2m(k,l,m∈N*) ______________
若m+n=p+q(p,q,m,n∈N*),则__________________
等差数列中下标成等差数列的项仍成等差数列
若{an},{bn}是等差数列,则{pan+qbn}(n∈N*)是等差数列
ak+al=2am
am+an=ap+aq
和的性质 任意连续m项的和构成的数列Sm,S2m-Sm,__________,…仍为等差数列
等差数列{an},{bn}的前n项和Sn,Tn之间的关系为=__________
等差数列的增减性:d>0时为__________数列,且当a1<0时前n项和Sn有最小值;d<0时为________数列,且当a1>0时前n项和Sn有最大值
S3m-S2m
递增
递减
1.设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
C
基础小测
2.(2020届云南师范大学附属中学高三上学期第一次月考)在等差数列{an}中,a5+a13=40,则a7+a8+a9+a10+a11=( )
A.40 B.60 C.80 D.100
D
考点突破
[例1] (2019全国卷Ⅰ,9)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5 B.an=3n-10
C.Sn=2n2-8n D.Sn=n2-2n
A
考点一 等差数列的基本量计算(高考热度:★★★)
1.等差数列运算问题的一般解法:先设出首项a1和公差d,然后由通项公式或前n项和公式转化为方程(组)求解.
2.等差数列的通项公式及前n项和公式,共涉及五个量a1,an,d,n,Sn,已知其中三个就能求出另外两个,体现了方程的思想.
方法总结
1.(多选题)已知等差数列{an}的前n项和为Sn,若S7=a4,则( )
A.a1+a3=0 B.a3+a5=0
C.S3=S4 D.S4=S5
BC
考点微练
2.若Sn是等差数列{an}的前n项和,且a2+a9+a19=6,则a10=________,S19=________.
2
38
考点二 等差数列的判定和证明(高考热度:★★★)
[例2] (2019湖北高三4月份调研考试)已知数列{an}满足a2-a1=1,其前n项和为Sn,当n≥2时,Sn-1-1,Sn,Sn+1成等差数列.
(1)求证:{an}为等差数列;
(2)若Sn=0,Sn+1=4 ,求n.
等差数列的判定与证明方法
方法 解读 适合题型
定义法 对于数列{an},an-an-1(n≥2,n∈N*)为同一常数 {an}是等差数列 解答题中的证明问题
等差中项法 2an-1=an+an-2(n≥3,n∈N*)成立 {an}是等差数列 通项公式法 an=pn+q(p,q为常数)对任意的正整数n都成立 {an}是等差数列 选择、填空题中的判定问题
前n项和公式法 验证Sn=An2+Bn(A,B为常数)对任意的正整数n都成立 {an}是等差数列
方法总结
如果要证明一个数列是等差数列,则必须用定义法或等差中项法.判断时易忽视定义中从第2项起,以后每项与前一项的差是同一常数,即易忽视验证a2-a1=d这一关键条件.
易错提醒
考点微练
已知数列{an}满足a1=6,an+1= (n∈N*).
(1)求证:数列是等差数列;
(2)求数列{lg an}的前n项和Tn.
[例3] (2020届广东珠海高三9月月考)已知等差数列{an}的前n项和为Sn,且S5=S10,则a11+a5=( )
A.0 B.5 C.8 D.16
A
考点三 等差数列的性质(高考热度:★★★)
等差数列{an}中,若a4+a6+a13+a15=20,则a10-a12的值是( )
A.4 B.5 C.6 D.8
A
对点变式
[例4] 设等差数列{an}的前n项和为Sn. 若S3=9,S6=27,则S9=( )
A.45 B.54
C.72 D.81
B
利用等差数列项的性质解决基本量的运算,体现了整体求值思想,应用时常将am+an=2ap(m+n=2p,m,n,p∈N*)与am+an=ap+aq(m+n=p+q,m,n,p,q∈N*)相结合,可减少运算量.
方法点拨
方法点拨
在等差数列{an}中,依据题意应用其前n项和的性质解题能比较简便地求出结果,常用的性质有数列Sm,S2m-Sm,S3m-S2m,…也是等差数列,且S2n=n(a1+a2n)=…=n(an+an+1),S2n-1=(2n-1)an.
1.已知等差数列{an}的前n项和为Sn,S7=14,an-3=28(n>7),Sn=225,则n=( )
A.8 B.9 C.15 D.17
C
考点微练
2.(2020届山东德州上学期期中)等差数列{an},{bn}的前n项和分别为Sn,Tn,且=,则=________.
考点四 等差数列前n项和的最值问题(高考热度:★★)
[例5] (2020届山东模拟)在①b1+b3=a2,②a4=b4,③S5=-25这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,求k的值;若k不存在,说明理由.
设等差数列{an}的前n项和为Sn,{bn}是等比数列,________,b1=a5,b2=3,b5=-81,是否存在k,使得Sk>Sk+1且Sk+1(1)函数法:利用等差数列前n项和的函数表达式Sn=an2+bn,通过配方或借助图象求二次函数最值的方法求解.
(2)邻项变号法:
①当a1>0,d<0时,满足的项数m使得Sn取得最大值为Sm;
②当a1<0,d>0时,满足的项数m使得Sn取得最小值为Sm.
求等差数列前n项和Sn最值的2种方法
技法点拨
1.已知等差数列{an}的公差为-2,前n项和为Sn.若a2,a3,a4为某三角形的三边长,且该三角形有一个内角为120°,则Sn的最大值为( )
A.5 B.11 C.20 D.25
D
考点微练
C
2.等差数列{an}的前n项和为Sn,已知a1=13,S3=S11,当Sn最大时,n的值为( )
A.5 B.6 C.7 D.8
解析过程见配套学案
通过本节课,你学会了什么?
等差数列
新课程标准 考向预测 1.通过实例,理解等差数列的概念. 2.探索并掌握等差数列的通项公式与前n项和的公式. 3.能在具体的问题情境中,发现数列的等差关系,并能用有关知识解决相应的问题. 4.体会等差数列与一次函数的关系. 命题角度 1.等差数列的基本运算
2.等差数列的判定与证明
3.等差数列的性质及应用
核心素养 逻辑推理、数学运算
基础梳理
一、等差数列的有关概念
如果一个数列从第2项起,每一项与它的前一项的差都等于____________,那么这个数列就叫做等差数列.这个常数叫做等差数列的_______,符号表示为_______________(n∈N*,d为常数).
定义
同一个常数
公差
an+1-an=d
要注意概念中的 “从第2项起”.如果一个数列不是从第2项起,而是从第3项或第4项起,每一项与它的前一项的差是同一个常数,那么此数列不是等差数列.
易错提示
若等差数列{an}的首项是a1,公差是d,则其通项公式为an=____________.
如果a,A,b成等差数列,那么A叫做a,b的等差中项,且A=__________.
等差中项
通项公式
a1+(n-1)d
前n项和公式
已知条件 前n项和公式
a1,an,n Sn=_______________
a1,d,n Sn=________________
C
基础小测
1.在等差数列11,8,5,…中,-49是它的( )
A.第19项 B.第20项
C.第21项 D.第22项
2.(2020届四川天府名校上学期第一轮联合质量测评)已知数列{an}满an+2-an+1=an+1-an(n∈N*),且a5=10,a7=14,则a2020-a2019=( )
A.2 B.1
C.-2 D.-1
A
1.等差数列的通项公式an=a1+(n-1)d,是关于n的一次函数.对应结论:(1)an=am+(n-m)d;(2)an=nd+(a1-d);(3)d= (n≠1)或d= (m≠n).
知识拓展
2.等差数列的前n项和公式Sn= =na1+,前一个公式(由倒序相加法推得)与中项有关(相当于n个等差中项之和),后一个公式是关于n的没有常数项的二次函数(Sn=An2+Bn).
二、等差数列的有关性质
类型 性质
项的性质 k+l=2m(k,l,m∈N*) ______________
若m+n=p+q(p,q,m,n∈N*),则__________________
等差数列中下标成等差数列的项仍成等差数列
若{an},{bn}是等差数列,则{pan+qbn}(n∈N*)是等差数列
ak+al=2am
am+an=ap+aq
和的性质 任意连续m项的和构成的数列Sm,S2m-Sm,__________,…仍为等差数列
等差数列{an},{bn}的前n项和Sn,Tn之间的关系为=__________
等差数列的增减性:d>0时为__________数列,且当a1<0时前n项和Sn有最小值;d<0时为________数列,且当a1>0时前n项和Sn有最大值
S3m-S2m
递增
递减
1.设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
C
基础小测
2.(2020届云南师范大学附属中学高三上学期第一次月考)在等差数列{an}中,a5+a13=40,则a7+a8+a9+a10+a11=( )
A.40 B.60 C.80 D.100
D
考点突破
[例1] (2019全国卷Ⅰ,9)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5 B.an=3n-10
C.Sn=2n2-8n D.Sn=n2-2n
A
考点一 等差数列的基本量计算(高考热度:★★★)
1.等差数列运算问题的一般解法:先设出首项a1和公差d,然后由通项公式或前n项和公式转化为方程(组)求解.
2.等差数列的通项公式及前n项和公式,共涉及五个量a1,an,d,n,Sn,已知其中三个就能求出另外两个,体现了方程的思想.
方法总结
1.(多选题)已知等差数列{an}的前n项和为Sn,若S7=a4,则( )
A.a1+a3=0 B.a3+a5=0
C.S3=S4 D.S4=S5
BC
考点微练
2.若Sn是等差数列{an}的前n项和,且a2+a9+a19=6,则a10=________,S19=________.
2
38
考点二 等差数列的判定和证明(高考热度:★★★)
[例2] (2019湖北高三4月份调研考试)已知数列{an}满足a2-a1=1,其前n项和为Sn,当n≥2时,Sn-1-1,Sn,Sn+1成等差数列.
(1)求证:{an}为等差数列;
(2)若Sn=0,Sn+1=4 ,求n.
等差数列的判定与证明方法
方法 解读 适合题型
定义法 对于数列{an},an-an-1(n≥2,n∈N*)为同一常数 {an}是等差数列 解答题中的证明问题
等差中项法 2an-1=an+an-2(n≥3,n∈N*)成立 {an}是等差数列 通项公式法 an=pn+q(p,q为常数)对任意的正整数n都成立 {an}是等差数列 选择、填空题中的判定问题
前n项和公式法 验证Sn=An2+Bn(A,B为常数)对任意的正整数n都成立 {an}是等差数列
方法总结
如果要证明一个数列是等差数列,则必须用定义法或等差中项法.判断时易忽视定义中从第2项起,以后每项与前一项的差是同一常数,即易忽视验证a2-a1=d这一关键条件.
易错提醒
考点微练
已知数列{an}满足a1=6,an+1= (n∈N*).
(1)求证:数列是等差数列;
(2)求数列{lg an}的前n项和Tn.
[例3] (2020届广东珠海高三9月月考)已知等差数列{an}的前n项和为Sn,且S5=S10,则a11+a5=( )
A.0 B.5 C.8 D.16
A
考点三 等差数列的性质(高考热度:★★★)
等差数列{an}中,若a4+a6+a13+a15=20,则a10-a12的值是( )
A.4 B.5 C.6 D.8
A
对点变式
[例4] 设等差数列{an}的前n项和为Sn. 若S3=9,S6=27,则S9=( )
A.45 B.54
C.72 D.81
B
利用等差数列项的性质解决基本量的运算,体现了整体求值思想,应用时常将am+an=2ap(m+n=2p,m,n,p∈N*)与am+an=ap+aq(m+n=p+q,m,n,p,q∈N*)相结合,可减少运算量.
方法点拨
方法点拨
在等差数列{an}中,依据题意应用其前n项和的性质解题能比较简便地求出结果,常用的性质有数列Sm,S2m-Sm,S3m-S2m,…也是等差数列,且S2n=n(a1+a2n)=…=n(an+an+1),S2n-1=(2n-1)an.
1.已知等差数列{an}的前n项和为Sn,S7=14,an-3=28(n>7),Sn=225,则n=( )
A.8 B.9 C.15 D.17
C
考点微练
2.(2020届山东德州上学期期中)等差数列{an},{bn}的前n项和分别为Sn,Tn,且=,则=________.
考点四 等差数列前n项和的最值问题(高考热度:★★)
[例5] (2020届山东模拟)在①b1+b3=a2,②a4=b4,③S5=-25这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,求k的值;若k不存在,说明理由.
设等差数列{an}的前n项和为Sn,{bn}是等比数列,________,b1=a5,b2=3,b5=-81,是否存在k,使得Sk>Sk+1且Sk+1
(2)邻项变号法:
①当a1>0,d<0时,满足的项数m使得Sn取得最大值为Sm;
②当a1<0,d>0时,满足的项数m使得Sn取得最小值为Sm.
求等差数列前n项和Sn最值的2种方法
技法点拨
1.已知等差数列{an}的公差为-2,前n项和为Sn.若a2,a3,a4为某三角形的三边长,且该三角形有一个内角为120°,则Sn的最大值为( )
A.5 B.11 C.20 D.25
D
考点微练
C
2.等差数列{an}的前n项和为Sn,已知a1=13,S3=S11,当Sn最大时,n的值为( )
A.5 B.6 C.7 D.8
解析过程见配套学案
通过本节课,你学会了什么?
