人教版(2019)数学选择性必修二 5_2导数的运算(1) 课件(共37张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 5_2导数的运算(1) 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:08:34 | ||
图片预览











文档简介
(共37张PPT)
导数的运算(1)
高二选择性必修二
本节目标
1.能根据定义求函数y=c,y=x,y=x2,y= ,y=的导数.
2.掌握基本初等函数的导数公式,并能进行简单的应用.
3.能利用导数的运算法则求函数的导数.
课前预习
(1)函数y=c,y=x,y=x-1,y=x2,y=的导数分别是什么?能否得出y=xn的导数公式?
(2)正余弦函数的导数公式、指数函数、对数函数的导数公式是什么?
(3)导数的四则运算法则是什么?在使用运算法则时的前提条件是什么?
预习课本P72~78,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若f (x)=0,则f ′(x)=0. ( )
(2)若f (x)=f (x)g(x),则F ′(x)=f ′(x)g′(x). ( )
(3)若f (x)=ln x,则f ′(e)=1. ( )
(4)若f (x)=x3+2x,那么f (x)在x0处的切线最小时x0=0. ( )
√
×
×
√
[ f (x)g(x)]′=f ′(x)g(x)+f (x)g′(x)
f ′(x)=. ∴f ′(e)=≠1
2. 等于( )
A. B.1 C.0 D.
C
常数的导数等于0.
3.(1) =________; (2)(xex)′=________.
=
=
(xex)′= ex+xex
= (1+x)ex
(1+x)ex
4.设函数f (x)在(0,+∞)内可导,且f (ex)=x+ex,则f ′(1)=________.
法一
令ex=t(t>0),则x=ln t.∵f (ex)=x+ex,∴f (t)=ln t+t,∴f ′(t)= +1,∴f ′(1)=1+1=2.
法二
对函数两边同时求导,得f ′(ex)=1+ex,令x=0,得f ′(e0)=f ′(1)=1+e0=2.
2
新知探究
1.几个常用函数的导数
(1) f (x)=c(常数),则f ′(x)=0;
(2) f (x)=x,则f ′(x)=1;
(3) f (x)=x2,则f ′(x)=2x;
(4) f (x)=x3,则f ′(x)=3x2;
(5) f (x)=,则f ′(x)=-;
(6) f (x)=,则f ′(x)= .
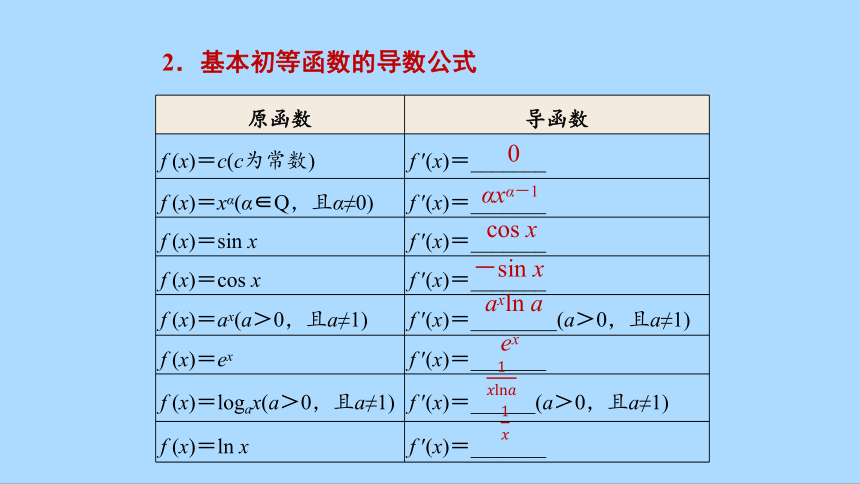
2.基本初等函数的导数公式
原函数 导函数
f (x)=c(c为常数) f ′(x)=_______
f (x)=xα(α∈Q,且α≠0) f ′(x)=_______
f (x)=sin x f ′(x)=_______
f (x)=cos x f ′(x)=_______
f (x)=ax(a>0,且a≠1) f ′(x)=________(a>0,且a≠1)
f (x)=ex f ′(x)=_______
f (x)=logax(a>0,且a≠1) f ′(x)=______(a>0,且a≠1)
f (x)=ln x f ′(x)=_______
0
αxα-1
cos x
-sin x
axln a
ex
(1)和差的导数
[f (x)±g(x)]′=___________.
(2)积的导数
①[f (x)g(x)]′=__________________;
②[cf (x)]′=___________.
(3)商的导数
=__________________(g(x)≠0).
3.导数的运算法则
f ′(x)±g′(x)
f ′(x)g(x)+f (x)g′(x)
cf ′(x)
题型突破
典例深度剖析 重点多维探究
题型一 利用导数公式求函数的导数
(1) y=cos ; (2) y= ;
(3) y= ; (4) y=lg x;
(5) y=5x; (6) y=cos .
[例1] 求下列函数的导数.
y=cos =,∴y′=0.
y==x-5,∴y′=5x-6.
y=
,
∴
y=cos ,
1.若所求函数符合导数公式,则直接利用公式求解.
2.对于不能直接利用公式的类型,一般遵循“先化简,再求导”的基本原则,避免不必要的运算失误.
3.要特别注意“与ln x”,“ax与logax”,“sin x与cos x”的导数区别.
方法总结
跟踪训练
1.求下列函数的导数:
(1)y=x; (2)y= (x>0); (3)y=sin(π-x).
y=
y=
y'=
y′=cos x
y=sin x
题型二 利用导数的运算法则求导数
1.如何求函数y=tan x的导数?
[探究问题]
y=tan x
=
y'=
=
=
[提示]
2.如何求函数y= sin 2x的导数?
[探究问题]
[提示]
y= sin 2x
= sin xcosx
= cosx+ sinx
=
=
(1)y=x3+sin x; (2)y=3x2+xcos x; (3)y= .
y′=(x3+sin x)′
=(x3)′+(sin x)′
=3x2+cos x.
y′=(3x2+xcos x)′
=(3x2)′+(xcos x)′
=3×2x+x′cos x+x(cos x)′
=6x+cos x-xsin x.
y=()
[例2] 求下列函数的导数:
多维探究
变式1 求函数y=x2 的导数.
y=x2
=x2
=2x
变式2 求函数y=xtan x的导数.
y′=(x·tan x)′=
=
=
=
仔细观察和分析函数的结构特征,紧扣求导运算法则,联系基本初等函数求导公式;
不具备求导法则条件的可适当进行恒等变形;
对较复杂的函数求导时,可先化简再求导;
对于对数函数的真数是根式或分式时,可先根据对数函数的性质将真数转化为有理式或整式,然后求导.
方法总结
利用导数的运算法则求导数的方法
[例3] (1)已知函数f (x)= ,若f ′(1)=,则实数a的值为( )
A.2 B.4 C.6 D.8
题型三 导数计算的综合应用
f ′(x)=
=
f ′(1)=
=
a=4
B
[例3] (2)已知函数f (x)=ax3+bx2+cx的图象过点(1,5),其导函数y=f ′(x)的图象如图所示,则函数f (x)的解析式为_________________.
故函数f (x)的解析式是f (x)=2x3-9x2+12x.
因为f ′(x)=3ax2+2bx+c,f ′(1)=0,f ′(2)=0,f (1)=5,
所以
解得
f (x)=2x3-9x2+12x
由于三次函数的导数是二次函数,因此将导数的计算与二次函数的图象和性质结合起来就很容易理解了.这类题目比较受青睐,解题时应回顾二次函数的单调性、最值、图象的对称轴、二次项系数对图象的影响等.
三次函数求导问题
方法总结
跟踪训练
3.如图中有一个图象是函数f (x)=x3+ax2+(a2-1)x+1(a∈R,且a≠0)的导函数的图象,则f (-1)=( )
(1) (2) (3)
A. B.- C. D.- 或
3.如图中有一个图象是函数f (x)=x3+ax2+(a2-1)x+1(a∈R,且a≠0)的导函数的图象,则f (-1)=( )
(1) (2) (3)
A. B.- C. D.- 或
f ′(x)=x2+2ax+a2-1=[x+(a+1)][x+(a-1)],图(1)与图(2)中,导函数的图象的对称轴都是y轴,此时a=0,与题设不符合,故图(3)中的图象是函数f (x)的导函数的图象.由图(3)知f ′(0)=0,由根与系数的关系得解得a=-1.故f (x)= x3-x2+1,所以f (-1)=-.
B
随堂检测
1.给出下列命题:
①y=ln 2,则y′= ; ②y= ,则y′|x=3=-;
③y=2x,则y′=2xln 2; ④y=log2x,则y′= .
其中正确命题的个数为( )
A.1 B.2 C.3 D.4
×
√
√
√
C
2.下列函数满足f ′(x)=f (x)的是( )
A.f (x)=ex B.f (x)=cos x
C.f (x)=sin x D.f (x)=ln x
A
3.已知f (x)=xα(α∈Q且α≠0),若f ′(1)= ,则α等于( )
A. B. C. D.
D
4.函数y=sin x+ex在点(0,1)处的切线方程为___________.
当x=0时,y=sin 0+e0=1,
即点(0,1)在函数y=sin x+ex的曲线上.
y=sin x+ex的导数y′=cos x+ex,
在点(0,1)处的切线斜率为k=cos 0+e0=2,
即在点(0,1)处的切线方程为2x-y+1=0.
2x-y+1=0
5.求下列函数的导数:
(1)y= ;
(2)y=log2x2-log2x;
∵y=log2x2-log2x=log2x,
∴y′=(log2x)′= .
5.求下列函数的导数:
(3)y= ;
法一
5.求下列函数的导数:
(3) y= ;
法二
5.求下列函数的导数:
(4) y=-2sin (1-2cos2).
y=-2sin (1-2cos2)
=2sin cos
=sin
=cos
=2sin (2cos2-1)
本课小结
1.利用常见函数的导数公式可以比较简捷地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
2.有些函数可先化简再应用公式求导,如求y=1-2sin2的导数,因为y=1-2sin2 =cos x,所以y′=(cos x)′=-sin x.
3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
通过本节课,你学会了什么?
导数的运算(1)
高二选择性必修二
本节目标
1.能根据定义求函数y=c,y=x,y=x2,y= ,y=的导数.
2.掌握基本初等函数的导数公式,并能进行简单的应用.
3.能利用导数的运算法则求函数的导数.
课前预习
(1)函数y=c,y=x,y=x-1,y=x2,y=的导数分别是什么?能否得出y=xn的导数公式?
(2)正余弦函数的导数公式、指数函数、对数函数的导数公式是什么?
(3)导数的四则运算法则是什么?在使用运算法则时的前提条件是什么?
预习课本P72~78,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若f (x)=0,则f ′(x)=0. ( )
(2)若f (x)=f (x)g(x),则F ′(x)=f ′(x)g′(x). ( )
(3)若f (x)=ln x,则f ′(e)=1. ( )
(4)若f (x)=x3+2x,那么f (x)在x0处的切线最小时x0=0. ( )
√
×
×
√
[ f (x)g(x)]′=f ′(x)g(x)+f (x)g′(x)
f ′(x)=. ∴f ′(e)=≠1
2. 等于( )
A. B.1 C.0 D.
C
常数的导数等于0.
3.(1) =________; (2)(xex)′=________.
=
=
(xex)′= ex+xex
= (1+x)ex
(1+x)ex
4.设函数f (x)在(0,+∞)内可导,且f (ex)=x+ex,则f ′(1)=________.
法一
令ex=t(t>0),则x=ln t.∵f (ex)=x+ex,∴f (t)=ln t+t,∴f ′(t)= +1,∴f ′(1)=1+1=2.
法二
对函数两边同时求导,得f ′(ex)=1+ex,令x=0,得f ′(e0)=f ′(1)=1+e0=2.
2
新知探究
1.几个常用函数的导数
(1) f (x)=c(常数),则f ′(x)=0;
(2) f (x)=x,则f ′(x)=1;
(3) f (x)=x2,则f ′(x)=2x;
(4) f (x)=x3,则f ′(x)=3x2;
(5) f (x)=,则f ′(x)=-;
(6) f (x)=,则f ′(x)= .
2.基本初等函数的导数公式
原函数 导函数
f (x)=c(c为常数) f ′(x)=_______
f (x)=xα(α∈Q,且α≠0) f ′(x)=_______
f (x)=sin x f ′(x)=_______
f (x)=cos x f ′(x)=_______
f (x)=ax(a>0,且a≠1) f ′(x)=________(a>0,且a≠1)
f (x)=ex f ′(x)=_______
f (x)=logax(a>0,且a≠1) f ′(x)=______(a>0,且a≠1)
f (x)=ln x f ′(x)=_______
0
αxα-1
cos x
-sin x
axln a
ex
(1)和差的导数
[f (x)±g(x)]′=___________.
(2)积的导数
①[f (x)g(x)]′=__________________;
②[cf (x)]′=___________.
(3)商的导数
=__________________(g(x)≠0).
3.导数的运算法则
f ′(x)±g′(x)
f ′(x)g(x)+f (x)g′(x)
cf ′(x)
题型突破
典例深度剖析 重点多维探究
题型一 利用导数公式求函数的导数
(1) y=cos ; (2) y= ;
(3) y= ; (4) y=lg x;
(5) y=5x; (6) y=cos .
[例1] 求下列函数的导数.
y=cos =,∴y′=0.
y==x-5,∴y′=5x-6.
y=
,
∴
y=cos ,
1.若所求函数符合导数公式,则直接利用公式求解.
2.对于不能直接利用公式的类型,一般遵循“先化简,再求导”的基本原则,避免不必要的运算失误.
3.要特别注意“与ln x”,“ax与logax”,“sin x与cos x”的导数区别.
方法总结
跟踪训练
1.求下列函数的导数:
(1)y=x; (2)y= (x>0); (3)y=sin(π-x).
y=
y=
y'=
y′=cos x
y=sin x
题型二 利用导数的运算法则求导数
1.如何求函数y=tan x的导数?
[探究问题]
y=tan x
=
y'=
=
=
[提示]
2.如何求函数y= sin 2x的导数?
[探究问题]
[提示]
y= sin 2x
= sin xcosx
= cosx+ sinx
=
=
(1)y=x3+sin x; (2)y=3x2+xcos x; (3)y= .
y′=(x3+sin x)′
=(x3)′+(sin x)′
=3x2+cos x.
y′=(3x2+xcos x)′
=(3x2)′+(xcos x)′
=3×2x+x′cos x+x(cos x)′
=6x+cos x-xsin x.
y=()
[例2] 求下列函数的导数:
多维探究
变式1 求函数y=x2 的导数.
y=x2
=x2
=2x
变式2 求函数y=xtan x的导数.
y′=(x·tan x)′=
=
=
=
仔细观察和分析函数的结构特征,紧扣求导运算法则,联系基本初等函数求导公式;
不具备求导法则条件的可适当进行恒等变形;
对较复杂的函数求导时,可先化简再求导;
对于对数函数的真数是根式或分式时,可先根据对数函数的性质将真数转化为有理式或整式,然后求导.
方法总结
利用导数的运算法则求导数的方法
[例3] (1)已知函数f (x)= ,若f ′(1)=,则实数a的值为( )
A.2 B.4 C.6 D.8
题型三 导数计算的综合应用
f ′(x)=
=
f ′(1)=
=
a=4
B
[例3] (2)已知函数f (x)=ax3+bx2+cx的图象过点(1,5),其导函数y=f ′(x)的图象如图所示,则函数f (x)的解析式为_________________.
故函数f (x)的解析式是f (x)=2x3-9x2+12x.
因为f ′(x)=3ax2+2bx+c,f ′(1)=0,f ′(2)=0,f (1)=5,
所以
解得
f (x)=2x3-9x2+12x
由于三次函数的导数是二次函数,因此将导数的计算与二次函数的图象和性质结合起来就很容易理解了.这类题目比较受青睐,解题时应回顾二次函数的单调性、最值、图象的对称轴、二次项系数对图象的影响等.
三次函数求导问题
方法总结
跟踪训练
3.如图中有一个图象是函数f (x)=x3+ax2+(a2-1)x+1(a∈R,且a≠0)的导函数的图象,则f (-1)=( )
(1) (2) (3)
A. B.- C. D.- 或
3.如图中有一个图象是函数f (x)=x3+ax2+(a2-1)x+1(a∈R,且a≠0)的导函数的图象,则f (-1)=( )
(1) (2) (3)
A. B.- C. D.- 或
f ′(x)=x2+2ax+a2-1=[x+(a+1)][x+(a-1)],图(1)与图(2)中,导函数的图象的对称轴都是y轴,此时a=0,与题设不符合,故图(3)中的图象是函数f (x)的导函数的图象.由图(3)知f ′(0)=0,由根与系数的关系得解得a=-1.故f (x)= x3-x2+1,所以f (-1)=-.
B
随堂检测
1.给出下列命题:
①y=ln 2,则y′= ; ②y= ,则y′|x=3=-;
③y=2x,则y′=2xln 2; ④y=log2x,则y′= .
其中正确命题的个数为( )
A.1 B.2 C.3 D.4
×
√
√
√
C
2.下列函数满足f ′(x)=f (x)的是( )
A.f (x)=ex B.f (x)=cos x
C.f (x)=sin x D.f (x)=ln x
A
3.已知f (x)=xα(α∈Q且α≠0),若f ′(1)= ,则α等于( )
A. B. C. D.
D
4.函数y=sin x+ex在点(0,1)处的切线方程为___________.
当x=0时,y=sin 0+e0=1,
即点(0,1)在函数y=sin x+ex的曲线上.
y=sin x+ex的导数y′=cos x+ex,
在点(0,1)处的切线斜率为k=cos 0+e0=2,
即在点(0,1)处的切线方程为2x-y+1=0.
2x-y+1=0
5.求下列函数的导数:
(1)y= ;
(2)y=log2x2-log2x;
∵y=log2x2-log2x=log2x,
∴y′=(log2x)′= .
5.求下列函数的导数:
(3)y= ;
法一
5.求下列函数的导数:
(3) y= ;
法二
5.求下列函数的导数:
(4) y=-2sin (1-2cos2).
y=-2sin (1-2cos2)
=2sin cos
=sin
=cos
=2sin (2cos2-1)
本课小结
1.利用常见函数的导数公式可以比较简捷地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
2.有些函数可先化简再应用公式求导,如求y=1-2sin2的导数,因为y=1-2sin2 =cos x,所以y′=(cos x)′=-sin x.
3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
通过本节课,你学会了什么?
