人教版(2019)数学选择性必修二 5_2导数的运算(2) 课件(共37张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 5_2导数的运算(2) 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 977.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
导数的运算(2)
高二选择性必修二
本节目标
1.了解复合函数的概念.
2.理解复合函数的求导法则,并能求简单的复合函数的导数.
课前预习
(1) 复合函数的定义是什么?
(2) 复合函数的求导法则是什么?
预习课本P78~81,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1) 函数y=sin(πx)的复合过程是y=sin u,u=πx.( )
(2) f (x)=ln(3x-1)则f ′(x)= . ( )
(3) f (x)=x2cos2x,则f ′(x)=2xcos2x+2x2sin2x.( )
√
×
×
f ′(x)=
f ′(x)=2xcos2x-2x2sin2x
2.函数y= 的导数是( )
A. B.
C.- D.-
y′=
C
3.下列对函数的求导正确的是( )
A.y=(1-2x)3,则y′=3(1-2x)2
B.y=log2(2x+1),则y′=
C.y=cos ,则y′= sin
D.y=22x-1,则y′=22xln 2
y′=-6(1-2x)2
×
y′=
×
y′=-sin
×
√
D
新知探究
1.复合函数的概念
一般地,对于两个函数y=f (u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f (u)和u=g(x)的复合函数,记作____________.
y=f (g(x))
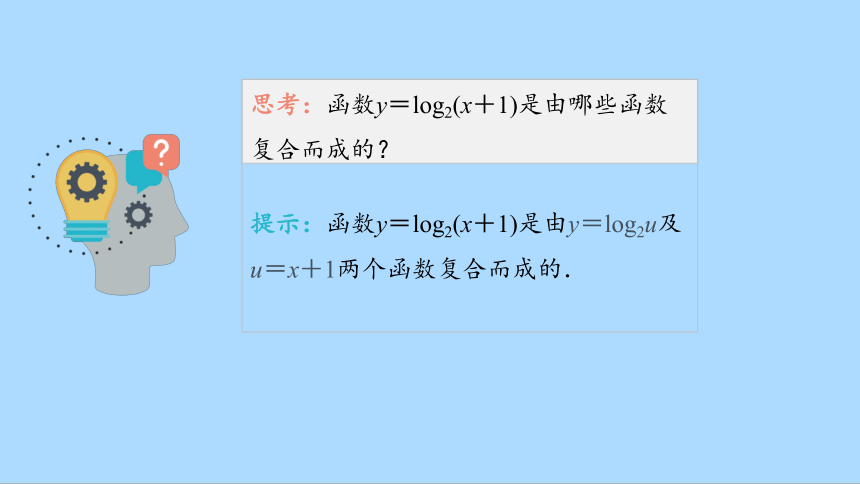
思考:函数y=log2(x+1)是由哪些函数复合而成的?
提示:函数y=log2(x+1)是由y=log2u及u=x+1两个函数复合而成的.
2.复合函数的求导法则
复合函数y=f (g(x))的导数和函数y=f (u),u=g(x)的导数间的关系为y′x=________,即y对x的导数等于______________________________.
y′u·u′x
y对u的导数与u对x的导数的乘积
题型突破
典例深度剖析 重点多维探究
题型一 复合函数的导数
[例1] 求下列函数的导数:
(1)y=e2x+1; (2)y= ;
(3)y=5log2(1-x); (4)y= .
[例1] 求下列函数的导数:
(2)y= ;
函数y=e2x+1可看作函数y=eu和u=2x+1的复合函数,
y′x=y′u·ux′
=(eu)′(2x+1)′
=2eu
=2e2x+1.
函数y=可看作函数y=u-3和u=2x-1的复合函数,
y′x=y′u·ux′
=(u-3)′(2x-1)′
=-6u-4
=-6(2x-1)-4
=- .
(1)y=e2x+1;
[例1] 求下列函数的导数:
(3) y=5log2(1-x);
(4) y= .
函数y=5log2(1-x)可看作函数y=5log2u和u=1-x的复合函数,
y′x=y′u·u′x
=(5log2u)′·(1-x)′
=
= .
(ln 3x)′=×(3x)′= .
y′=
=
= .
(1)不能正确区分所给函数是否为复合函数;
(2)若是复合函数,不能正确判断它是由哪些基本初等函数复合而成.
解答此类问题常犯两个错误
易错提醒
复合函数求导的步骤
分解
求导
回代
选定中间变量,正确分解复合关系,即说明函数关系y=f(u), u=g(x)
分步求导(弄清每一步求导是哪个变量对哪个变量求导),要特别注意中间变量对自变量求导,即先求y′u,再求u′x.
计算y′u·u′x,并把中间变量转化为自变量的函数.
方法总结
跟踪训练
1.求下列函数的导数:
(1) y=103x-2;
(2) y=ln(ex+x2);
令u=3x-2,则y=10u.
y′x=y′u·u′x
=10uln 10·(3x-2)′
=3×103x-2ln 10.
令u=ex+x2,则y=ln u.
y′x=y′u·u′x
= ·(ex+x2)′
= .
跟踪训练
1.求下列函数的导数:
(3) y=x.
y′=(x)′
= +x()′
= +
= .
[例2] 求下列函数的导数:
(1)y=cos ; (2)y=x2+tan x.
题型二 三角函数型函数的导数
∵y=cos=cos sin -cos2
= sin x- (1+cos x)
= (sin x-cos x)- ,
∴y′=[(sin x-cos x)- ]′
= (sin x-cos x)′
= (cos x+sin x).
∵y=x2+ ,
∴y′=(x2)′+()′
=2x+
=2x+ .
对三角函数型函数的求导,往往需要利用三角恒等变换公式,对函数式进行化简,再进行求导.
复合函数的求导法则熟悉后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,从外层开始由外到内逐层求导.
三角函数型函数的求导要求
方法总结
跟踪训练
′
y′=(sin3x+sin x3)′
=(sin3x)′+(sin x3)′
=3sin2xcos x+cos x3·3x2
=3sin2xcos x+3x2cos x3.
2.求下列函数的导数:
(1) y=sin2 ; (2) y=sin3x+sin x3;
跟踪训练
2.求下列函数的导数:
(3) y=cos4x-sin4x.
y=cos4x-sin4x
=(cos2x+sin2x)(cos2x-sin2x)
=cos 2x,
∴y′=(cos 2x)′=-2sin 2x.
[提示]
设P(x0,y0),由题意可知= ,
所以=1,即x0=0,
∴点P(0,1).
由点P(0,1)在直线y=x+b上可知b=1.
题型三 导数运算法则的综合应用
[探究问题]
1.若直线y=x+b与曲线y=ex相切于点P,你能求出切点坐标及b的值吗?
2.曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,你能求出a,b的值吗?
[提示]
∵y′=aex+ln x+1,
∴y′|x=1=ae+1,
∴2=ae+1,
∴a=e-1.
∴切点为(1,1),
将(1,1)代入y=2x+b,得1=2+b,
∴b=-1,故a=,b=-1.
[探究问题]
[例3] (1)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
A. B.2
C.3 D.0
设曲线y=ln(2x-1)在点(x0,y0)处的切线与直线2x-y+3=0平行.
∵y′=,∴= =2,解得x0=1,
∴y0=ln(2-1)=0,即切点坐标为(1,0).
∴切点(1,0)到直线2x-y +3=0的距离为d= =,
即曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是.
A
[例3] (2)设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=________.
令y=f (x),则曲线y=eax在点(0,1)处的切线的斜率为f ′(0),又切线与直线x+2y+1=0垂直,所以f ′(0)=2.
因为f (x)=eax,所以f ′(x)=(eax)′=eax·(ax)′=aeax,
所以f ′(0)=ae0=a,
故a=2.
2
多维探究
变式1 曲线y=ln(2x-1)上的点到直线2x-y+m=0的最小距离为2,求m的值.
由题意可知,设切点P(x0,y0),
则==2,
∴x0=1,即切点P(1,0),
∴ =2,解得m=8或-12.
即实数m的值为8或-12.
变式2 若直线y=kx+b是y=ln x+2的切线,也是y=ln(x+1)的切线,求b的值.
函数y=ln x+2的导函数为y′=,函数y=ln(x+1)的导函数为y′= .
设曲线y=ln x+2和曲线y=ln(x+1)上的切点横坐标分别为m,n,
则该直线方程可以写成y=·(x-m)+ln m+2,
也可以写成y= (x-n)+ln(n+1).
整理后对比得
解得
因此b=1-ln 2.
(1)求曲线过某一定点的切线方程或斜率时,首先应判断所给定点是不是切点,如果不是,需将切点坐标设出.
(2)切点既在原函数的图象上也在切线上,可将切点坐标代入两者的函数解析式建立方程组.
(3)如果切线的斜率存在,那么函数在切点处的导数值等于切线的斜率,这是求切线方程最重要的条件.
(4)与曲线只有一个公共点的直线不一定是曲线的切线,曲线的切线与曲线的公共点不一定只有一个.
利用导数的几何意义解题时的注意点
要点提醒
随堂检测
1.函数y=(x2-1)n的复合过程正确的是( )
A.y=un,u=x2-1 B.y=(u-1)n,u=x2
C.y=tn,t=(x2-1)n D.y=(t-1)n,t=x2-1
A
2.函数y=x2cos 2x的导数为( )
A.y′=2xcos 2x-x2sin 2x B.y′=2xcos 2x-2x2sin 2x
C.y′=x2cos 2x-2xsin 2x D.y′=2xcos 2x+2x2sin 2x
y′=(x2)′cos 2x+x2(cos 2x)′
=2xcos 2x+x2(-sin 2x)·(2x)′
=2xcos 2x-2x2sin 2x.
B
3.已知f (x)=ln(3x-1),则f ′(1)=________.
f ′(x)= ×(3x-1)′= ,
f ′(1)= = .
4.已知f (x)=xe-x,则f (x)在x=2处的切线斜率是________.
∵f (x)=xe-x,
∴f ′(x)=e-x-xe-x=(1-x)e-x,
∴f ′(2)=-.
根据导数的几何意义知f (x)在x=2处的切线斜率为k=f ′(2)=- .
-
y′=e2x·(2x)′
=e2x·2
=2e2x.
y′=3(1-3x)2(1-3x)′
=-9(1-3x)2
或y′=-81x2+54x-9.
5.求下列函数的导数:
(1)y=e2x; (2)y=(1-3x)3.
本课小结
1.求复合函数的导数的注意点
①分解的函数通常为基本初等函数;
②求导时分清是对哪个变量求导;
③计算结果尽量简洁.
2.和与差的运算法则可以推广
[f (x1)±f (x2)±…±f (xn)]′=f ′(x1)±f ′(x2)±…±f ′(xn).
通过本节课,你学会了什么?
导数的运算(2)
高二选择性必修二
本节目标
1.了解复合函数的概念.
2.理解复合函数的求导法则,并能求简单的复合函数的导数.
课前预习
(1) 复合函数的定义是什么?
(2) 复合函数的求导法则是什么?
预习课本P78~81,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1) 函数y=sin(πx)的复合过程是y=sin u,u=πx.( )
(2) f (x)=ln(3x-1)则f ′(x)= . ( )
(3) f (x)=x2cos2x,则f ′(x)=2xcos2x+2x2sin2x.( )
√
×
×
f ′(x)=
f ′(x)=2xcos2x-2x2sin2x
2.函数y= 的导数是( )
A. B.
C.- D.-
y′=
C
3.下列对函数的求导正确的是( )
A.y=(1-2x)3,则y′=3(1-2x)2
B.y=log2(2x+1),则y′=
C.y=cos ,则y′= sin
D.y=22x-1,则y′=22xln 2
y′=-6(1-2x)2
×
y′=
×
y′=-sin
×
√
D
新知探究
1.复合函数的概念
一般地,对于两个函数y=f (u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f (u)和u=g(x)的复合函数,记作____________.
y=f (g(x))
思考:函数y=log2(x+1)是由哪些函数复合而成的?
提示:函数y=log2(x+1)是由y=log2u及u=x+1两个函数复合而成的.
2.复合函数的求导法则
复合函数y=f (g(x))的导数和函数y=f (u),u=g(x)的导数间的关系为y′x=________,即y对x的导数等于______________________________.
y′u·u′x
y对u的导数与u对x的导数的乘积
题型突破
典例深度剖析 重点多维探究
题型一 复合函数的导数
[例1] 求下列函数的导数:
(1)y=e2x+1; (2)y= ;
(3)y=5log2(1-x); (4)y= .
[例1] 求下列函数的导数:
(2)y= ;
函数y=e2x+1可看作函数y=eu和u=2x+1的复合函数,
y′x=y′u·ux′
=(eu)′(2x+1)′
=2eu
=2e2x+1.
函数y=可看作函数y=u-3和u=2x-1的复合函数,
y′x=y′u·ux′
=(u-3)′(2x-1)′
=-6u-4
=-6(2x-1)-4
=- .
(1)y=e2x+1;
[例1] 求下列函数的导数:
(3) y=5log2(1-x);
(4) y= .
函数y=5log2(1-x)可看作函数y=5log2u和u=1-x的复合函数,
y′x=y′u·u′x
=(5log2u)′·(1-x)′
=
= .
(ln 3x)′=×(3x)′= .
y′=
=
= .
(1)不能正确区分所给函数是否为复合函数;
(2)若是复合函数,不能正确判断它是由哪些基本初等函数复合而成.
解答此类问题常犯两个错误
易错提醒
复合函数求导的步骤
分解
求导
回代
选定中间变量,正确分解复合关系,即说明函数关系y=f(u), u=g(x)
分步求导(弄清每一步求导是哪个变量对哪个变量求导),要特别注意中间变量对自变量求导,即先求y′u,再求u′x.
计算y′u·u′x,并把中间变量转化为自变量的函数.
方法总结
跟踪训练
1.求下列函数的导数:
(1) y=103x-2;
(2) y=ln(ex+x2);
令u=3x-2,则y=10u.
y′x=y′u·u′x
=10uln 10·(3x-2)′
=3×103x-2ln 10.
令u=ex+x2,则y=ln u.
y′x=y′u·u′x
= ·(ex+x2)′
= .
跟踪训练
1.求下列函数的导数:
(3) y=x.
y′=(x)′
= +x()′
= +
= .
[例2] 求下列函数的导数:
(1)y=cos ; (2)y=x2+tan x.
题型二 三角函数型函数的导数
∵y=cos=cos sin -cos2
= sin x- (1+cos x)
= (sin x-cos x)- ,
∴y′=[(sin x-cos x)- ]′
= (sin x-cos x)′
= (cos x+sin x).
∵y=x2+ ,
∴y′=(x2)′+()′
=2x+
=2x+ .
对三角函数型函数的求导,往往需要利用三角恒等变换公式,对函数式进行化简,再进行求导.
复合函数的求导法则熟悉后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,从外层开始由外到内逐层求导.
三角函数型函数的求导要求
方法总结
跟踪训练
′
y′=(sin3x+sin x3)′
=(sin3x)′+(sin x3)′
=3sin2xcos x+cos x3·3x2
=3sin2xcos x+3x2cos x3.
2.求下列函数的导数:
(1) y=sin2 ; (2) y=sin3x+sin x3;
跟踪训练
2.求下列函数的导数:
(3) y=cos4x-sin4x.
y=cos4x-sin4x
=(cos2x+sin2x)(cos2x-sin2x)
=cos 2x,
∴y′=(cos 2x)′=-2sin 2x.
[提示]
设P(x0,y0),由题意可知= ,
所以=1,即x0=0,
∴点P(0,1).
由点P(0,1)在直线y=x+b上可知b=1.
题型三 导数运算法则的综合应用
[探究问题]
1.若直线y=x+b与曲线y=ex相切于点P,你能求出切点坐标及b的值吗?
2.曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,你能求出a,b的值吗?
[提示]
∵y′=aex+ln x+1,
∴y′|x=1=ae+1,
∴2=ae+1,
∴a=e-1.
∴切点为(1,1),
将(1,1)代入y=2x+b,得1=2+b,
∴b=-1,故a=,b=-1.
[探究问题]
[例3] (1)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
A. B.2
C.3 D.0
设曲线y=ln(2x-1)在点(x0,y0)处的切线与直线2x-y+3=0平行.
∵y′=,∴= =2,解得x0=1,
∴y0=ln(2-1)=0,即切点坐标为(1,0).
∴切点(1,0)到直线2x-y +3=0的距离为d= =,
即曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是.
A
[例3] (2)设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=________.
令y=f (x),则曲线y=eax在点(0,1)处的切线的斜率为f ′(0),又切线与直线x+2y+1=0垂直,所以f ′(0)=2.
因为f (x)=eax,所以f ′(x)=(eax)′=eax·(ax)′=aeax,
所以f ′(0)=ae0=a,
故a=2.
2
多维探究
变式1 曲线y=ln(2x-1)上的点到直线2x-y+m=0的最小距离为2,求m的值.
由题意可知,设切点P(x0,y0),
则==2,
∴x0=1,即切点P(1,0),
∴ =2,解得m=8或-12.
即实数m的值为8或-12.
变式2 若直线y=kx+b是y=ln x+2的切线,也是y=ln(x+1)的切线,求b的值.
函数y=ln x+2的导函数为y′=,函数y=ln(x+1)的导函数为y′= .
设曲线y=ln x+2和曲线y=ln(x+1)上的切点横坐标分别为m,n,
则该直线方程可以写成y=·(x-m)+ln m+2,
也可以写成y= (x-n)+ln(n+1).
整理后对比得
解得
因此b=1-ln 2.
(1)求曲线过某一定点的切线方程或斜率时,首先应判断所给定点是不是切点,如果不是,需将切点坐标设出.
(2)切点既在原函数的图象上也在切线上,可将切点坐标代入两者的函数解析式建立方程组.
(3)如果切线的斜率存在,那么函数在切点处的导数值等于切线的斜率,这是求切线方程最重要的条件.
(4)与曲线只有一个公共点的直线不一定是曲线的切线,曲线的切线与曲线的公共点不一定只有一个.
利用导数的几何意义解题时的注意点
要点提醒
随堂检测
1.函数y=(x2-1)n的复合过程正确的是( )
A.y=un,u=x2-1 B.y=(u-1)n,u=x2
C.y=tn,t=(x2-1)n D.y=(t-1)n,t=x2-1
A
2.函数y=x2cos 2x的导数为( )
A.y′=2xcos 2x-x2sin 2x B.y′=2xcos 2x-2x2sin 2x
C.y′=x2cos 2x-2xsin 2x D.y′=2xcos 2x+2x2sin 2x
y′=(x2)′cos 2x+x2(cos 2x)′
=2xcos 2x+x2(-sin 2x)·(2x)′
=2xcos 2x-2x2sin 2x.
B
3.已知f (x)=ln(3x-1),则f ′(1)=________.
f ′(x)= ×(3x-1)′= ,
f ′(1)= = .
4.已知f (x)=xe-x,则f (x)在x=2处的切线斜率是________.
∵f (x)=xe-x,
∴f ′(x)=e-x-xe-x=(1-x)e-x,
∴f ′(2)=-.
根据导数的几何意义知f (x)在x=2处的切线斜率为k=f ′(2)=- .
-
y′=e2x·(2x)′
=e2x·2
=2e2x.
y′=3(1-3x)2(1-3x)′
=-9(1-3x)2
或y′=-81x2+54x-9.
5.求下列函数的导数:
(1)y=e2x; (2)y=(1-3x)3.
本课小结
1.求复合函数的导数的注意点
①分解的函数通常为基本初等函数;
②求导时分清是对哪个变量求导;
③计算结果尽量简洁.
2.和与差的运算法则可以推广
[f (x1)±f (x2)±…±f (xn)]′=f ′(x1)±f ′(x2)±…±f ′(xn).
通过本节课,你学会了什么?
