人教版(2019)数学选择性必修二 5_3_2函数的极值与最大(小)值(3) 课件(共48张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 5_3_2函数的极值与最大(小)值(3) 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:11:11 | ||
图片预览











文档简介
(共48张PPT)
函数的极值与最大(小)值(3)
高二选择性必修二
本节目标
1.能用导数解决函数的零点问题.
2.体会导数在解决实际问题中的作用.
3.能利用导数解决简单的实际问题.
课前预习
(1) 画函数f (x)的大致图象可按哪几个的步骤进行?
(2) 用导数解决优化问题的基本思路有哪些?
预习课本P95~97,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)用导数研究实际问题要先求定义域. ( )
(2)方程xex=2有两个不相等的实数根. ( )
(3)做一个容积为256 m3的方底无盖水箱,所用材料最省时,它的高为4 m. ( )
√
×
√
1.判断正误(正确的打“√”,错误的打“×”)
(2)方程xex=2有两个不相等的实数根. ( )
×
令y=xex,则y′=ex(x+1).
由于x>-1时,y′>0,x<-1时,y′<0.
∴x=-1时y=xex取到最小值-.
结合单调性及变化趋势画出如图所示,
由图可以看出y=xex与y=2只有一个交点,
故方程只有一个解.
1.判断正误(正确的打“√”,错误的打“×”)
(3)做一个容积为256 m3的方底无盖水箱,所用材料最省时,它的高为4 m. ( )
√
设底的边长为x m,则高为.
那么需材料的面积为x2+4x× =x2+.
令y=x2+,∴y′=2x- .
令y′=0得x=8.又x>8时y′>0,x<8时y′<0,
∴x=8时用料最省,这时高h= =4(m).
2.炼油厂某分厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为f (x)=x3-x2+8(0≤x≤5),那么原油温度的瞬时变化率的最小值是( )
A.8 B. C.-1 D.-8
由题意,f ′(x)=x2-2x=(x-1)2-1,
∵0≤x≤5,
∴x=1时,f ′(x)的最小值为-1,
即原油温度的瞬时变化率的最小值是-1.
C
3.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=- x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
A.13万件 B.11万件
C.9万件 D.7万件
由题意得,y′=-x2+81,
令y′=0,解得x=9或x=-9(舍去).
当0<x<9时,y′>0;当x>9时,y′<0.
故当x=9时,y取得极大值,也是最大值.
C
4.某产品的销售收入y1(万元)关于产量x(千台)的函数关系式为y1=17x2,生产成本y2(万元)关于产量x(千台)的函数关系式为y2=2x3-x2,已知x>0,为使利润最大,应生产该产品________千台.
利润y=y1-y2=17x2-(2x3-x2)=18x2-2x3(x>0).
y′=36x-6x2,
由y′=36x-6x2=6x(6-x)=0,得x=6(x=0舍去),
当x∈(0,6)时,y′>0,当x∈(6,+∞)时,y′<0,
函数在(0,6)上为增函数,在(6,+∞)上为减函数.
则当x=6时,y有最大值.
6
新知探究
1.函数图象的画法
函数f (x)的图象直观地反映了函数f (x)的性质.通常,按如下步骤画出函数f (x)的图象:
(1)求出函数f (x)的_________;
(2)求导数f ′(x)及函数f ′(x)的_______;
(3)用f ′(x)的零点将f (x)的定义域划分成若干个区间,列表给出f ′(x)在各区间上的______,并得出f (x)的_______与_______;
(4)确定f (x)的图象所经过的一些特殊点,以及图象的________;
(5)画出f (x)的大致图象.
定义域
零点
正负
单调性
极值
变化趋势
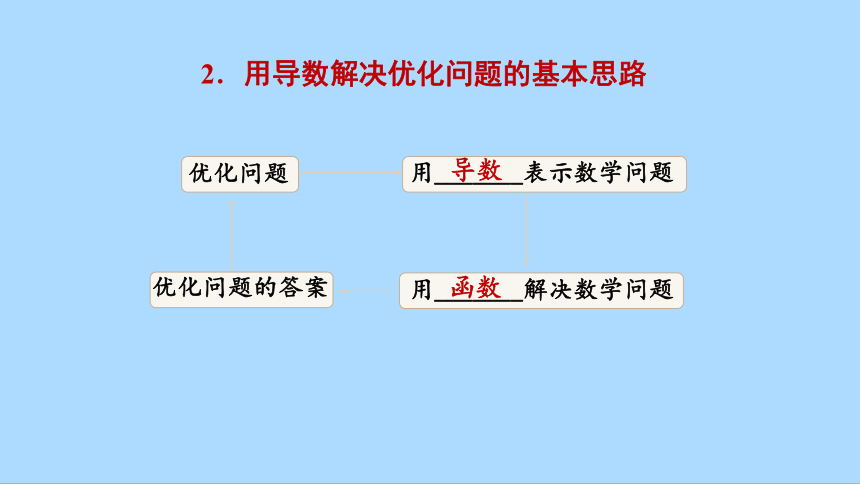
2.用导数解决优化问题的基本思路
优化问题
用_______表示数学问题
用_______解决数学问题
优化问题的答案
导数
函数
解决生活中优化问题应注意什么?
[提示]
(1)在建立函数模型时,应根据实际问题确定出函数的定义域.
(2)求实际问题的最大(小)值时,一定要从问题的实际意义去考查,不符合实际意义的应舍去,如:长度、宽度应大于0,销售价为正数等.
思考
题型突破
典例深度剖析 重点多维探究
题型一 利用导数研究函数的图象
[例1] 函数y= (其中e为自然对数的底数)的大致图象是( )
由函数y=可知,当x=0时,y=0,排除C;当x<0时,y<0,排除A;
y′= ,当x<3时,y′>0,当x>3时,y′<0,
∴函数在(0,+∞)上先增后减.
B
法一
题型一 利用导数研究函数的图象
[例1] 函数y= (其中e为自然对数的底数)的大致图象是( )
B
法二
当x=0时,y=0,排除C;
当x<0时,y<0,排除A;
当x→+∞时,y→0.
根据解析式判断函数的图象时,综合应用各种方法:如判断函数的奇偶性,定义域、特殊值和单调性,有时还要用导数研究函数的极值点,甚至最值等.
由解析式研究图象常用的方法
方法总结
跟踪训练
1.函数f (x)=-2x2的图象大致为( )
∵f (x)=f (-x),
当x>0时,f ′(x)= ·2x-4x,
令f ′(x)=0,则
2x(-2)=0 x= ∈(0,1),
且f ()=2-2ln 2>0,
∴当x>0时,f (x)>0,且只有一个极值点,
∴排除B,C,D.
A
题型二 用导数研究方程的根
[例2] 设函数f (x)= -kln x,k>0.
(1)求f (x)的单调区间和极值;
(2)证明:若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
[例2] 设函数f (x)= -kln x,k>0.
(1)求f (x)的单调区间和极值;
由f (x)=-kln x(k>0)得f ′(x)=x-= ,
由f ′(x)=0解得x=.
f (x)与f ′(x)在区间(0,+∞)上的变化情况如下表:
x (0,) (,+∞)
f ′(x) - 0 +
f (x) ↘ ↗
所以f (x)的单调递减区间是(0, ),单调递增区间是(,+∞),f (x)在x=处取得极小值f ()=,无极大值.
[例2] 设函数f (x)= -kln x,k>0.
(2)证明:若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
所以x=是f (x)在区间(1,]上的唯一零点.
由(1)知,f (x)在区间(0,+∞)上的最小值为f ()= .
因为f (x)存在零点,所以≤0,从而k≥e.
当k=e时,f (x)在区间(1,)上单调递减,且f ()=0,
当k>e时,f (x)在区间(0,)上单调递减,且f (1)=>0,f ()= <0,
所以f (x)在区间(1,]上仅有一个零点.
综上可知,若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
与函数零点有关的问题,往往利用导数研究函数的单调性和极值点,并结合特殊点判断函数的大致图象,讨论图象与x轴的位置关系(或者转化为两个熟悉函数的图象交点问题)确定参数的取值范围.
与函数零点有关的问题
方法总结
跟踪训练
2.若方程ax=x(a>0,a≠1)有两个不等实根,求实数a的取值范围.
当x∈(0, e)时,f ′(x)>0,f (x)单调递增;
结合图象可知,若方程ax=x(a>0,a≠1)有两个不等实根,则a>1.
由ax=x知x>0,故x·ln a-ln x=0 ln a=,
令f (x)= (x>0),则f ′(x)= .
当x∈(e,+∞)时,f ′(x)<0,f (x)单调递减,
故当x=e时,f (x)取得最大值f (e)=,即ln a<,即a<.
画出函数y=ax(a>0,a≠1)与y=x的图象,
综上可知,实数a的取值范围为.
题型三 导数在生活实际问题中应用
角度1 用料最省、成本(费用)最低问题
[例3] 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f (x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f (x)的表达式;
(2)隔热层修建多厚时,总费用f (x)达到最小?并求最小值.
[例3] 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f (x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f (x)的表达式;
由题设,每年能源消耗费用为C(x)=(0≤x≤10),
再由C(0)=8,得k=40,因此C(x)= .
而建造费用为C1(x)=6x.
最后得隔热层建造费用与20年的能源消耗费用之和为
f (x)=20C(x)+C1(x)=20×+6x= +6x(0≤x≤10).
[例3] (2)隔热层修建多厚时,总费用f (x)达到最小?并求最小值.
f ′(x)=6- ,
令f ′(x)=0,即=6,解得x=5或x=- (舍去).
当00,
故x=5是f (x)的最小值点,
对应的最小值为f (5)=6×5+=70.
当隔热层修建5 cm厚时,总费用达到最小值70万元.
在实际生活中关于用料最省、费用最低、损耗最小、用时最短等问题,一般情况下都需要利用导数求解相应函数的最小值.若求出极值点(注意根据实际意义舍去不合适的极值点)后,函数在该点附近满足“左减右增”,则此时唯一的极小值就是所求的函数的最小值.
求解优化问题中的最小值问题的思路
方法总结
跟踪训练
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
设船每小时航行所需的燃料费为y1元,比例系数为k(k>0),则y1=kv2.
∵当v=12时,y1=720,∴720=k·122,得k=5,则y1=5v2.
设全程燃料费为y元,由题意,得y=y1· = ,
∴y′= = .
令y′=0,解得v=0(舍去)或v=16.
若v0≥16,当v∈(8,16)时,y′<0,y为减函数;
当v∈(16,v0]时,y′>0,y为增函数.
故当v=16千米/时时,y取得极小值,也是最小值,此时全程燃料费最省.
若v0<16,则v∈(8,v0],且y′<0,y在(8,v0]上为减函数.
故当v=v0时,y取得最小值,此时全程燃料费最省.
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
综上可得,若v0≥16,则当v=16千米/时时,全程燃料费最省,为32000元;若v0<16,则当v=v0时,全程燃料费最省,为元.
角度2 利润最大、效率最高问题
1.在实际问题中,如果在定义域内函数只有一个极值点,则函数在该点处取最值吗?
[提示] 根据函数的极值与单调性的关系可以判断,函数在该点处取最值,并且极小值点对应最小值,极大值点对应最大值.
[探究问题]
2.你能列举几个有关利润的等量关系吗?
[提示]
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.
[探究问题]
[例4] 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
[例4] 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
因为x=5时,y=11,
所以+10=11,a=2.
[例4] (2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由(1)知,该商品每日的销售量y= +10(x-6)2,
所以商场每日销售该商品所获得的利润
f (x)=(x-3) =2+10(x-3)(x-6)2,3<x<6,
从而,f ′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)·(x-6),
于是,当x变化时,f ′(x),f (x)的变化情况如下表:
x (3,4) 4 (4,6)
f ′(x) + 0 -
f (x) ↗ 极大值42 ↘
[例4] (2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由上表可得,x=4是函数f (x)在区间(3,6)内的极大值点,也是最大值点,
所以,当x=4时,函数f (x)取得最大值,且最大值等于42.
故当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
利润最大问题是生活中常见的一类问题,一般根据“利润=收入-成本”建立函数关系式,再利用导数求最大值.
解此类问题需注意两点:
①价格要大于或等于成本,否则就会亏本;
②销量要大于0,否则不会获利.
方法总结
跟踪训练
4.某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为x(0<x<1),那么月平均销售量减少的百分率为x2,记改进工艺后该电子公司销售该配件的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
4.某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为x(0<x<1),那么月平均销售量减少的百分率为x2,记改进工艺后该电子公司销售该配件的月平均利润是y(元).
(1)写出y与x的函数关系式;
改进工艺后,每个配件的销售价为20(1+x)元,月平均销售量为a(1-x2)件,
则月平均利润y=a(1-x2)·[20(1+x)-15](元),
∴y与x的函数关系式为y=5a(1+4x-x2-4x3)(0<x<1).
4. (2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
y′=5a(4-2x-12x2),令y′=0,得x1=,x2=-(舍),
当0<x< 时,y′>0; <x<1时,y′<0,
∴函数y=5a(1+4x-x2-4x3)(0<x<1)在x=时取得极大值也是最大值,
故改进工艺后,每个配件的销售价为20×(1+)=30元时,
该电子公司销售该配件的月平均利润最大.
随堂检测
1.某箱子的体积与底面边长x的关系为V(x)=x2(0A.30 B.40 C.50 D.60
V′(x)=-x2+60x=-x(x-40),
因为0<x<60,所以当0<x<40时,V′(x)>0,此时V(x)单调递增;
当40所以V(40)是V(x)的极大值,
即当箱子的体积最大时,箱子底面边长为40.
B
2.设函数f (x)的导函数为f ′(x),若f (x)为偶函数,且在(0,1)上存在极大值,则f ′(x)的图象可能为( )
f (x)为偶函数,则其导数f ′(x)为奇函数,结合函数图象可以排除B、D.
又由于函数f (x)在(0,1)上存在极大值,则其导数图象在(0,1)上存在零点,且零点左侧导数值符号为正,右侧导数值符号为负,结合选项可以排除A
C
3.若方程x3-3x+m=0在[0,2]上有解,则实数m的取值范围是( )
A.[-2,2] B.[0,2]
C.[-2,0] D.(-∞,-2)∪(2,+∞)
方程x3-3x+m=0在[0,2]上有解,则-m=x3-3x,x∈[0,2],求实数m的取值范围可转化为求函数的值域问题.
令y=x3-3x,x∈[0,2],则y′=3x2-3,
令y′>0,解得x>1,因此函数在[0,1)上单调递减,在(1,2]上单调递增,
又x=1时,y=-2;x=2时,y=2;x=0时,y=0,
∴函数y=x3-3x,x∈[0,2]的值域是[-2,2],
故-m∈[-2,2],∴m∈[-2,2]
A
4.电动自行车的耗电量y与速度x之间的关系为y= x3- x2-40x(x>0),为使耗电量最小,则其速度应定为________.
由题设知y′=x2-39x-40,
令y′>0,解得x>40或x<-1,
故函数y= x3-x2-40x(x>0)在[40,+∞)上递增,在(0,40]上递减.
∴当x=40时,y取得最小值.
由此得为使耗电量最小,则其速度应定为40.
40
1.运用零点存在性定理求解零点存在或者零点个数问题的关键是寻找合适的零点区间.还可以采取分离变量法把零点个数问题转化为函数图象的交点个数问题.
本课小结
2.利用导数解决优化问题,往往归结为函数的最大值或最小值问题.
解题的一般方法如下:
(1)设出变量找出函数关系式,确定定义域;
(2)若函数f (x)在定义域内只有一个极值点x0,则不需与端点处函数值比较,f (x0)即是所求的最大值或最小值.
本课小结
3.“恒成立”问题的解决往往要转化为函数的最值问题.
通过本节课,你学会了什么?
函数的极值与最大(小)值(3)
高二选择性必修二
本节目标
1.能用导数解决函数的零点问题.
2.体会导数在解决实际问题中的作用.
3.能利用导数解决简单的实际问题.
课前预习
(1) 画函数f (x)的大致图象可按哪几个的步骤进行?
(2) 用导数解决优化问题的基本思路有哪些?
预习课本P95~97,思考并完成以下问题
课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)用导数研究实际问题要先求定义域. ( )
(2)方程xex=2有两个不相等的实数根. ( )
(3)做一个容积为256 m3的方底无盖水箱,所用材料最省时,它的高为4 m. ( )
√
×
√
1.判断正误(正确的打“√”,错误的打“×”)
(2)方程xex=2有两个不相等的实数根. ( )
×
令y=xex,则y′=ex(x+1).
由于x>-1时,y′>0,x<-1时,y′<0.
∴x=-1时y=xex取到最小值-.
结合单调性及变化趋势画出如图所示,
由图可以看出y=xex与y=2只有一个交点,
故方程只有一个解.
1.判断正误(正确的打“√”,错误的打“×”)
(3)做一个容积为256 m3的方底无盖水箱,所用材料最省时,它的高为4 m. ( )
√
设底的边长为x m,则高为.
那么需材料的面积为x2+4x× =x2+.
令y=x2+,∴y′=2x- .
令y′=0得x=8.又x>8时y′>0,x<8时y′<0,
∴x=8时用料最省,这时高h= =4(m).
2.炼油厂某分厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为f (x)=x3-x2+8(0≤x≤5),那么原油温度的瞬时变化率的最小值是( )
A.8 B. C.-1 D.-8
由题意,f ′(x)=x2-2x=(x-1)2-1,
∵0≤x≤5,
∴x=1时,f ′(x)的最小值为-1,
即原油温度的瞬时变化率的最小值是-1.
C
3.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=- x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
A.13万件 B.11万件
C.9万件 D.7万件
由题意得,y′=-x2+81,
令y′=0,解得x=9或x=-9(舍去).
当0<x<9时,y′>0;当x>9时,y′<0.
故当x=9时,y取得极大值,也是最大值.
C
4.某产品的销售收入y1(万元)关于产量x(千台)的函数关系式为y1=17x2,生产成本y2(万元)关于产量x(千台)的函数关系式为y2=2x3-x2,已知x>0,为使利润最大,应生产该产品________千台.
利润y=y1-y2=17x2-(2x3-x2)=18x2-2x3(x>0).
y′=36x-6x2,
由y′=36x-6x2=6x(6-x)=0,得x=6(x=0舍去),
当x∈(0,6)时,y′>0,当x∈(6,+∞)时,y′<0,
函数在(0,6)上为增函数,在(6,+∞)上为减函数.
则当x=6时,y有最大值.
6
新知探究
1.函数图象的画法
函数f (x)的图象直观地反映了函数f (x)的性质.通常,按如下步骤画出函数f (x)的图象:
(1)求出函数f (x)的_________;
(2)求导数f ′(x)及函数f ′(x)的_______;
(3)用f ′(x)的零点将f (x)的定义域划分成若干个区间,列表给出f ′(x)在各区间上的______,并得出f (x)的_______与_______;
(4)确定f (x)的图象所经过的一些特殊点,以及图象的________;
(5)画出f (x)的大致图象.
定义域
零点
正负
单调性
极值
变化趋势
2.用导数解决优化问题的基本思路
优化问题
用_______表示数学问题
用_______解决数学问题
优化问题的答案
导数
函数
解决生活中优化问题应注意什么?
[提示]
(1)在建立函数模型时,应根据实际问题确定出函数的定义域.
(2)求实际问题的最大(小)值时,一定要从问题的实际意义去考查,不符合实际意义的应舍去,如:长度、宽度应大于0,销售价为正数等.
思考
题型突破
典例深度剖析 重点多维探究
题型一 利用导数研究函数的图象
[例1] 函数y= (其中e为自然对数的底数)的大致图象是( )
由函数y=可知,当x=0时,y=0,排除C;当x<0时,y<0,排除A;
y′= ,当x<3时,y′>0,当x>3时,y′<0,
∴函数在(0,+∞)上先增后减.
B
法一
题型一 利用导数研究函数的图象
[例1] 函数y= (其中e为自然对数的底数)的大致图象是( )
B
法二
当x=0时,y=0,排除C;
当x<0时,y<0,排除A;
当x→+∞时,y→0.
根据解析式判断函数的图象时,综合应用各种方法:如判断函数的奇偶性,定义域、特殊值和单调性,有时还要用导数研究函数的极值点,甚至最值等.
由解析式研究图象常用的方法
方法总结
跟踪训练
1.函数f (x)=-2x2的图象大致为( )
∵f (x)=f (-x),
当x>0时,f ′(x)= ·2x-4x,
令f ′(x)=0,则
2x(-2)=0 x= ∈(0,1),
且f ()=2-2ln 2>0,
∴当x>0时,f (x)>0,且只有一个极值点,
∴排除B,C,D.
A
题型二 用导数研究方程的根
[例2] 设函数f (x)= -kln x,k>0.
(1)求f (x)的单调区间和极值;
(2)证明:若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
[例2] 设函数f (x)= -kln x,k>0.
(1)求f (x)的单调区间和极值;
由f (x)=-kln x(k>0)得f ′(x)=x-= ,
由f ′(x)=0解得x=.
f (x)与f ′(x)在区间(0,+∞)上的变化情况如下表:
x (0,) (,+∞)
f ′(x) - 0 +
f (x) ↘ ↗
所以f (x)的单调递减区间是(0, ),单调递增区间是(,+∞),f (x)在x=处取得极小值f ()=,无极大值.
[例2] 设函数f (x)= -kln x,k>0.
(2)证明:若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
所以x=是f (x)在区间(1,]上的唯一零点.
由(1)知,f (x)在区间(0,+∞)上的最小值为f ()= .
因为f (x)存在零点,所以≤0,从而k≥e.
当k=e时,f (x)在区间(1,)上单调递减,且f ()=0,
当k>e时,f (x)在区间(0,)上单调递减,且f (1)=>0,f ()= <0,
所以f (x)在区间(1,]上仅有一个零点.
综上可知,若f (x)存在零点,则f (x)在区间(1,]上仅有一个零点.
与函数零点有关的问题,往往利用导数研究函数的单调性和极值点,并结合特殊点判断函数的大致图象,讨论图象与x轴的位置关系(或者转化为两个熟悉函数的图象交点问题)确定参数的取值范围.
与函数零点有关的问题
方法总结
跟踪训练
2.若方程ax=x(a>0,a≠1)有两个不等实根,求实数a的取值范围.
当x∈(0, e)时,f ′(x)>0,f (x)单调递增;
结合图象可知,若方程ax=x(a>0,a≠1)有两个不等实根,则a>1.
由ax=x知x>0,故x·ln a-ln x=0 ln a=,
令f (x)= (x>0),则f ′(x)= .
当x∈(e,+∞)时,f ′(x)<0,f (x)单调递减,
故当x=e时,f (x)取得最大值f (e)=,即ln a<,即a<.
画出函数y=ax(a>0,a≠1)与y=x的图象,
综上可知,实数a的取值范围为.
题型三 导数在生活实际问题中应用
角度1 用料最省、成本(费用)最低问题
[例3] 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f (x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f (x)的表达式;
(2)隔热层修建多厚时,总费用f (x)达到最小?并求最小值.
[例3] 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f (x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f (x)的表达式;
由题设,每年能源消耗费用为C(x)=(0≤x≤10),
再由C(0)=8,得k=40,因此C(x)= .
而建造费用为C1(x)=6x.
最后得隔热层建造费用与20年的能源消耗费用之和为
f (x)=20C(x)+C1(x)=20×+6x= +6x(0≤x≤10).
[例3] (2)隔热层修建多厚时,总费用f (x)达到最小?并求最小值.
f ′(x)=6- ,
令f ′(x)=0,即=6,解得x=5或x=- (舍去).
当0
故x=5是f (x)的最小值点,
对应的最小值为f (5)=6×5+=70.
当隔热层修建5 cm厚时,总费用达到最小值70万元.
在实际生活中关于用料最省、费用最低、损耗最小、用时最短等问题,一般情况下都需要利用导数求解相应函数的最小值.若求出极值点(注意根据实际意义舍去不合适的极值点)后,函数在该点附近满足“左减右增”,则此时唯一的极小值就是所求的函数的最小值.
求解优化问题中的最小值问题的思路
方法总结
跟踪训练
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
设船每小时航行所需的燃料费为y1元,比例系数为k(k>0),则y1=kv2.
∵当v=12时,y1=720,∴720=k·122,得k=5,则y1=5v2.
设全程燃料费为y元,由题意,得y=y1· = ,
∴y′= = .
令y′=0,解得v=0(舍去)或v=16.
若v0≥16,当v∈(8,16)时,y′<0,y为减函数;
当v∈(16,v0]时,y′>0,y为增函数.
故当v=16千米/时时,y取得极小值,也是最小值,此时全程燃料费最省.
若v0<16,则v∈(8,v0],且y′<0,y在(8,v0]上为减函数.
故当v=v0时,y取得最小值,此时全程燃料费最省.
3.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?
综上可得,若v0≥16,则当v=16千米/时时,全程燃料费最省,为32000元;若v0<16,则当v=v0时,全程燃料费最省,为元.
角度2 利润最大、效率最高问题
1.在实际问题中,如果在定义域内函数只有一个极值点,则函数在该点处取最值吗?
[提示] 根据函数的极值与单调性的关系可以判断,函数在该点处取最值,并且极小值点对应最小值,极大值点对应最大值.
[探究问题]
2.你能列举几个有关利润的等量关系吗?
[提示]
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.
[探究问题]
[例4] 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
[例4] 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
因为x=5时,y=11,
所以+10=11,a=2.
[例4] (2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由(1)知,该商品每日的销售量y= +10(x-6)2,
所以商场每日销售该商品所获得的利润
f (x)=(x-3) =2+10(x-3)(x-6)2,3<x<6,
从而,f ′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)·(x-6),
于是,当x变化时,f ′(x),f (x)的变化情况如下表:
x (3,4) 4 (4,6)
f ′(x) + 0 -
f (x) ↗ 极大值42 ↘
[例4] (2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由上表可得,x=4是函数f (x)在区间(3,6)内的极大值点,也是最大值点,
所以,当x=4时,函数f (x)取得最大值,且最大值等于42.
故当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
利润最大问题是生活中常见的一类问题,一般根据“利润=收入-成本”建立函数关系式,再利用导数求最大值.
解此类问题需注意两点:
①价格要大于或等于成本,否则就会亏本;
②销量要大于0,否则不会获利.
方法总结
跟踪训练
4.某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为x(0<x<1),那么月平均销售量减少的百分率为x2,记改进工艺后该电子公司销售该配件的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
4.某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为x(0<x<1),那么月平均销售量减少的百分率为x2,记改进工艺后该电子公司销售该配件的月平均利润是y(元).
(1)写出y与x的函数关系式;
改进工艺后,每个配件的销售价为20(1+x)元,月平均销售量为a(1-x2)件,
则月平均利润y=a(1-x2)·[20(1+x)-15](元),
∴y与x的函数关系式为y=5a(1+4x-x2-4x3)(0<x<1).
4. (2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
y′=5a(4-2x-12x2),令y′=0,得x1=,x2=-(舍),
当0<x< 时,y′>0; <x<1时,y′<0,
∴函数y=5a(1+4x-x2-4x3)(0<x<1)在x=时取得极大值也是最大值,
故改进工艺后,每个配件的销售价为20×(1+)=30元时,
该电子公司销售该配件的月平均利润最大.
随堂检测
1.某箱子的体积与底面边长x的关系为V(x)=x2(0
V′(x)=-x2+60x=-x(x-40),
因为0<x<60,所以当0<x<40时,V′(x)>0,此时V(x)单调递增;
当40
即当箱子的体积最大时,箱子底面边长为40.
B
2.设函数f (x)的导函数为f ′(x),若f (x)为偶函数,且在(0,1)上存在极大值,则f ′(x)的图象可能为( )
f (x)为偶函数,则其导数f ′(x)为奇函数,结合函数图象可以排除B、D.
又由于函数f (x)在(0,1)上存在极大值,则其导数图象在(0,1)上存在零点,且零点左侧导数值符号为正,右侧导数值符号为负,结合选项可以排除A
C
3.若方程x3-3x+m=0在[0,2]上有解,则实数m的取值范围是( )
A.[-2,2] B.[0,2]
C.[-2,0] D.(-∞,-2)∪(2,+∞)
方程x3-3x+m=0在[0,2]上有解,则-m=x3-3x,x∈[0,2],求实数m的取值范围可转化为求函数的值域问题.
令y=x3-3x,x∈[0,2],则y′=3x2-3,
令y′>0,解得x>1,因此函数在[0,1)上单调递减,在(1,2]上单调递增,
又x=1时,y=-2;x=2时,y=2;x=0时,y=0,
∴函数y=x3-3x,x∈[0,2]的值域是[-2,2],
故-m∈[-2,2],∴m∈[-2,2]
A
4.电动自行车的耗电量y与速度x之间的关系为y= x3- x2-40x(x>0),为使耗电量最小,则其速度应定为________.
由题设知y′=x2-39x-40,
令y′>0,解得x>40或x<-1,
故函数y= x3-x2-40x(x>0)在[40,+∞)上递增,在(0,40]上递减.
∴当x=40时,y取得最小值.
由此得为使耗电量最小,则其速度应定为40.
40
1.运用零点存在性定理求解零点存在或者零点个数问题的关键是寻找合适的零点区间.还可以采取分离变量法把零点个数问题转化为函数图象的交点个数问题.
本课小结
2.利用导数解决优化问题,往往归结为函数的最大值或最小值问题.
解题的一般方法如下:
(1)设出变量找出函数关系式,确定定义域;
(2)若函数f (x)在定义域内只有一个极值点x0,则不需与端点处函数值比较,f (x0)即是所求的最大值或最小值.
本课小结
3.“恒成立”问题的解决往往要转化为函数的最值问题.
通过本节课,你学会了什么?
