人教版(2019)数学选择性必修二:第四章数列 章末复习 课件(共39张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二:第四章数列 章末复习 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:15:51 | ||
图片预览










文档简介
(共39张PPT)
第四章 数列章末复习
高二选择性必修二
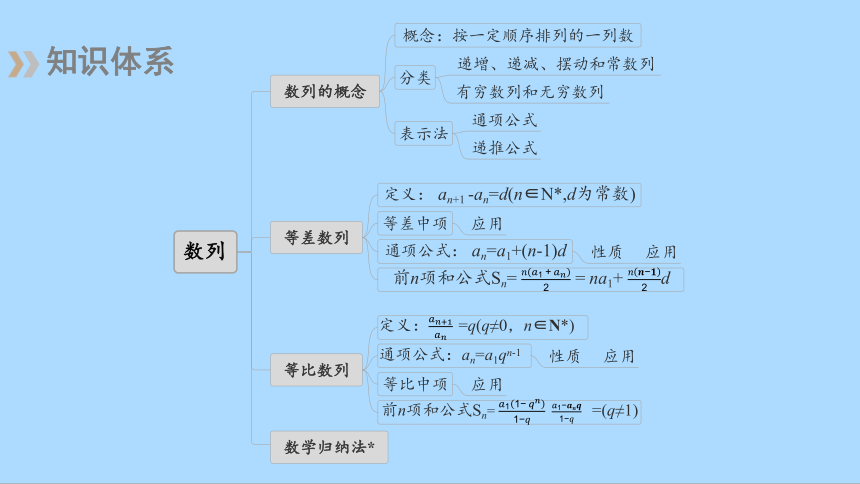
数列的概念
等差数列
等比数列
数学归纳法*
概念:按一定顺序排列的一列数
分类
递增、递减、摆动和常数列
有穷数列和无穷数列
表示法
通项公式
递推公式
定义: an+1 -an=d(n∈N*,d为常数)
等差中项
应用
通项公式: an=a1+(n-1)d
性质
应用
前n项和公式Sn= = na1+ d
定义:=q(q≠0,n∈N*)
通项公式:an=a1qn-1
性质
应用
等比中项
应用
前n项和公式Sn= = (q≠1)
数列
知识体系
题型突破
典例深度剖析 重点多维探究
题型一 求数列的通项公式
[例1] (1)已知等比数列{an}为递增数列,且=a10,2(an+an+2)=5an+1,则数列的通项公式an=( )
A.2n B.2n+1 C D.
由数列{an}为递增的等比数列,可知公比q>0,
而=a10>0,所以q>1,an>0.
由2(an+an+2)=5an+1,得2an+2anq2=5anq,
则2q2-5q+2=0,解得q=2或q=(舍去).
由=a10,得(a1q4)2=a1q9,解得a1=2.因此an=2n.
A
法一
题型一 求数列的通项公式
[例1] (1)已知等比数列{an}为递增数列,且=a10,2(an+an+2)=5an+1,则数列的通项公式an=( )
A.2n B.2n+1 C D.
A
法二
由等比数列{an}为递增数列知,公比q>0,
而=a10>0,所以an>0,q>1.
由条件得2=5,即2=5,解得q=2.
又由=a10,得(a1q4)2=a1q9,即a1=q=2,故an=2n.
题型一 求数列的通项公式
[例1] (2)已知数列{an}中,an+1=3an+4,且a1=1,求通项公式.
∵an+1=3an+4,
∴an+1+2=3(an+2).
令bn=an+2,∵b1=a1+2=3,
∴数列{bn}是首项为3,公比为3的等比数列,
则bn=3n,
∴an=3n-2.
法一
题型一 求数列的通项公式
[例1] (2)已知数列{an}中,an+1=3an+4,且a1=1,求通项公式.
∵an+1=3an+4, ①
∴an=3an-1+4(n≥2). ②
①-②,得an+1-an=3(an-an-1)(n≥2).
∵a2-a1=3+4-1=6,
∴数列{an+1-an}是首项为6,公比为3的等比数列,
即an+1-an=6×3n-1=2×3n,利用累加法得an=3n-2.
法二
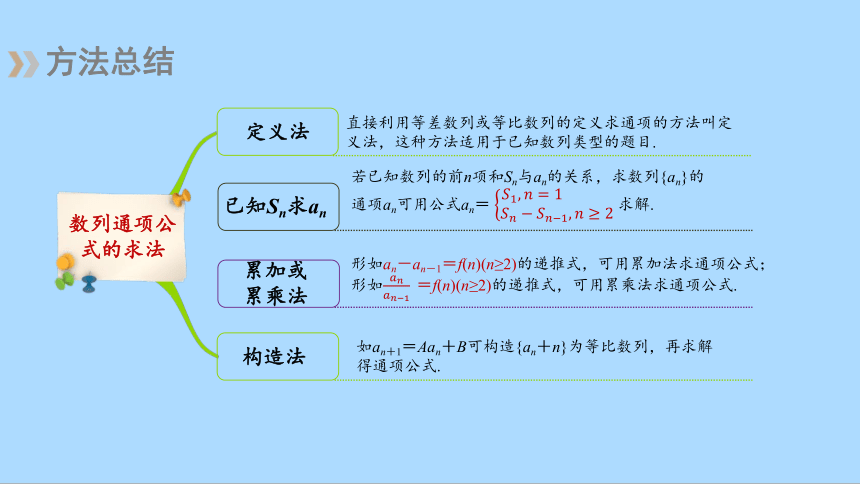
方法总结
累加或
累乘法
直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适用于已知数列类型的题目.
已知Sn求an
若已知数列的前n项和Sn与an的关系,求数列{an}的通项an可用公式an= 求解.
形如an-an-1=f(n)(n≥2)的递推式,可用累加法求通项公式;形如=f(n)(n≥2)的递推式,可用累乘法求通项公式.
构造法
如an+1=Aan+B可构造{an+n}为等比数列,再求解得通项公式.
定义法
数列通项公式的求法
跟踪训练
1.已知数列{an}的前n项和Sn=2n-an,求数列的通项公式an.
由a1=S1=2-a1,得a1=1.
当n≥2时,an=Sn-Sn-1=2n-an-[2(n-1)-an-1]=-an+2+an-1,
所以an= an-1+1,即an-2= (an-1-2).
令bn=an-2,则bn= bn-1,且b1=1-2=-1,
于是数列{bn}是首项为-1,公比为的等比数列,
所以bn=-1×()n-1=-()n-1 ,故an=2- ()n-1.
题型二 等差、等比数列的基本运算
[例2] 等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式;
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
[例2] 等比数列{an}中,已知a1=2,a4=16.
(1) 求数列{an}的通项公式;
设{an}的公比为q,
a1=2,a4=16
16=2q3
q=2
an=2×2n-1=2n
[例2] 等比数列{an}中,已知a1=2,a4=16.
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
由(1)得a3=8,a5=32,则b3=8,b5=32.
设{bn}的公差为d,则有
所以bn=-16+12(n-1)=12n-28.
所以数列{bn}的前n项和Sn= =6n2-22n.
解得
在等差数列和等比数列的通项公式an与前n项和公式Sn中,共涉及五个量:a1,an,n,d(或q),Sn,其中a1和d(或q)为基本量,“知三求二”是指将已知条件转换成关于a1,d(q),an,Sn,n的方程组,利用方程的思想求出需要的量,当然在求解中若能运用等差(比)数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.
方法总结
跟踪训练
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
(2)记{an}的前n项和为Sn,求Sn的最小值.
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
∵{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列,
∴(a3+8)2=(a2+10)(a4+6),
∴(-2+2d)2=d(-4+3d),解得d=2,
∴an=a1+(n-1)d=-10+2n-2=2n-12.
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(2)记{an}的前n项和为Sn,求Sn的最小值.
∴n=5或n=6时,Sn取最小值-30.
由a1=-10,d=2,得:
Sn=-10n+×2=n2-11n= ,
题型三 等差、等比数列的判定
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列;
(2)设cn= ,求证:{cn}是等差数列.
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列;
an+2=Sn+2-Sn+1=4an+1+2-4an-2=4an+1-4an.
=2.
因为S2=a1+a2=4a1+2,所以a2=5.
所以b1=a2-2a1=3.
所以数列{bn}是首项为3,公比为2的等比数列.
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(2)设cn= ,求证:{cn}是等差数列.
由(1)知bn=3·2n-1=an+1-2an,
所以=3.
所以cn+1-cn=3,且c1= =2,
所以数列{cn}是等差数列,公差为3,首项为2.
等差数列、等比数列的判断方法
(1)定义法
an+1-an=d(常数) {an}是等差数列;
=q(q为常数,q≠0) {an}是等比数列.
(2)中项公式法
2an+1=an+an+2 {an}是等差数列;
=an·an+2(an≠0) {an}是等比数列.
(3)通项公式法
an=kn+b(k,b是常数) {an}是等差数列;
an=c·qn(c,q为非零常数) {an}是等比数列.
(4)前n项和公式法
Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;
Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
跟踪训练
3.已知数列{an}满足a1=1,an+1=3an+1.
(1)证明是等比数列,并求{an}的通项公式;
(2)证明+ +…+ < .
3.已知数列{an}满足a1=1,an+1=3an+1.
(1)证明是等比数列,并求{an}的通项公式;
由an+1=3an+1得an+1+=3(an+ ).
因为a1+= ,
所以是首项为,公比为3的等比数列.
所以an+ = ,因此{an}的通项公式为an= .
3.已知数列{an}满足a1=1,an+1=3an+1.
(2)证明+ +…+ < .
由(1)知= .
因为当n≥1时,3n-1≥2×3n-1,所以≤ .
于是+ +…+ ≤1++…+ = (1- )< .
所以+ +…+ < .
题型四 等差、等比数列的性质
[例4] (1) (多选题)等差数列{an}的公差为d,前n项和为Sn,当首项a1和d变化时,a3+a8+a13是一个定值,则下列各数也为定值的有( )
A.a7 B.a8 C.S15 D.S16
由等差中项的性质可得a3+a8+a13=3a8为定值,
则a8为定值,S15= =15a8为定值,
但S16= =8不是定值.
BC
(2) (多选题)设等比数列{an}的公比为q,其前n项和为Sn,前n项积为Tn,并满足条件a1>1,a2019a2020>1, <0,下列结论正确的是( )
A.S2019C.T2020是数列{Tn}中的最大值 D.数列{Tn}无最大值
当q<0时,a2019a2020= q<0,不成立;
当q≥1时,a2019≥1,a2020>1, <0不成立;
故0<q<1,且a2019>1,0<a2020<1,故S2020>S2019,A正确;
a2019a2021-1= -1<0,故B正确;
T2019是数列{Tn}中的最大值,CD错误.
AB
(3)等比数列{an}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5=________.
由等比数列的性质知a1a5=a2a4= =4 a3=2,
5
log2a1+log2a2+log2a3+log2a4+log2a5
=log2(a1a2a3a4a5)
=log2
=5log22
=5.
(1)等差数列、等比数列公式和性质的灵活应用;
(2)对于计算解答题注意基本量及方程思想的运用;
(3)注重问题的转化,由非等差数列、非等比数列构造出新的等差数列或等比数列,以便利用相关公式和性质解题;
(4)当题目中出现多个数列时,既要纵向考察单一数列的项与项之间的关系,又要横向考察各数列之间的内在联系.
解决等差、等比数列有关问题的几点注意
方法总结
跟踪训练
4.(1)已知{an}为等比数列,且an>0,a2a4+2a3a5+a4a6=25,求a3+a5的值.
因为数列{an}为等比数列,
∴a2a4=,a4a6= ,
又∵a2a4+2a3a5+a4a6=25,
∴ +2a3a5+ =25,而an>0,
故a3+a5=5.
跟踪训练
4. (2)在等比数列{an}中,已知Sn=48,S2n=60,求S3n.
根据数列{an}为等比数列,
则Sn,S2n-Sn,S3n-S2n,…成等比数列,
即48,60-48,S3n-60,…成等比数列,
∴48×(S3n-60)=122,
解得S3n=63.
题型五 数列求和
1.若数列{cn}是公差为d的等差数列,数列{bn}是公比为q(q≠1)的等比数列,且an=cn+bn,如何求数列{an}的前n项和?
[探究问题]
[提示]
数列{an}的前n项和等于数列{cn}和{bn}的前n项和的和.
2.有些数列单独看求和困难,但相邻项结合后会变成熟悉的等差数列、等比数列求和.试用此种方法求和:
12-22+32-42+…+992-1002.
[探究问题]
[提示]
12-22+32-42+…+992-1002=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2+3+4+…+99+100)=-5050.
3.我们知道= -,试用此公式求和: + +…+ .
[提示] 由= -得 + +…+
=1-+ - +…+ - =1- = .
[探究问题]
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和.
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1) 求an;
当n≥2时,an=Sn-Sn-1=k(cn-cn-1),
则a6=k(c6-c5),a3=k(c3-c2),= =c3=8,
∴c=2.
∵a2=4,即k(c2-c1)=4,
∴an=2n.
当n=1时,a1=S1=2.
综上所述,an=2n(n∈N*).
解得k=2,
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(2)求数列{nan}的前n项和.
nan=n·2n,
则Tn=2+2·22+3·23+…+n·2n,
2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,
两式作差得-Tn=2+22+23+…+2n-n·2n+1,
∴Tn=2+(n-1)·2n+1.
多维探究
变式1 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
求数列{n+an}的前n项和Tn .
Tn=1+2+2+22+3+23+…+n+2n
=(1+2+3+…+n)+(2+22+…+2n)
= +
=2n+1-2+
变式2 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3. 求数列的前n项和Tn.
Tn= + + +…+ , ①
Tn= + +…+ +, ②
Tn= + + +…+ - = =1--,
∴Tn=2- - =2- .
①-②得:
变式3 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3. 设Sn是数列{an}的前n项和,bn= ,求数列{bn}的前n项和Tn.
由(1)知an=2n,
∴Sn= = =2n+1-2.
因为bn= = = -,
所以Tn=b1+b2+…+bn=(-)+(-)+…+(-)= - = - = .
数列求和问题一般转化为等差数列或等比数列的前n项和问题或已知公式的数列求和,不能转化的再根据数列通项公式的特点选择恰当的方法求解.一般常见的求和方法有:
(1)公式法:利用等差数列或等比数列前n项和公式.
(2)分组求和法:把一个数列分成几个可以直接求和的数列.
(3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和.
(4)错位相减法:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和.
(5)倒序相加法:例如,等差数列前n项和公式的推导.
方法总结
第四章 数列章末复习
高二选择性必修二
数列的概念
等差数列
等比数列
数学归纳法*
概念:按一定顺序排列的一列数
分类
递增、递减、摆动和常数列
有穷数列和无穷数列
表示法
通项公式
递推公式
定义: an+1 -an=d(n∈N*,d为常数)
等差中项
应用
通项公式: an=a1+(n-1)d
性质
应用
前n项和公式Sn= = na1+ d
定义:=q(q≠0,n∈N*)
通项公式:an=a1qn-1
性质
应用
等比中项
应用
前n项和公式Sn= = (q≠1)
数列
知识体系
题型突破
典例深度剖析 重点多维探究
题型一 求数列的通项公式
[例1] (1)已知等比数列{an}为递增数列,且=a10,2(an+an+2)=5an+1,则数列的通项公式an=( )
A.2n B.2n+1 C D.
由数列{an}为递增的等比数列,可知公比q>0,
而=a10>0,所以q>1,an>0.
由2(an+an+2)=5an+1,得2an+2anq2=5anq,
则2q2-5q+2=0,解得q=2或q=(舍去).
由=a10,得(a1q4)2=a1q9,解得a1=2.因此an=2n.
A
法一
题型一 求数列的通项公式
[例1] (1)已知等比数列{an}为递增数列,且=a10,2(an+an+2)=5an+1,则数列的通项公式an=( )
A.2n B.2n+1 C D.
A
法二
由等比数列{an}为递增数列知,公比q>0,
而=a10>0,所以an>0,q>1.
由条件得2=5,即2=5,解得q=2.
又由=a10,得(a1q4)2=a1q9,即a1=q=2,故an=2n.
题型一 求数列的通项公式
[例1] (2)已知数列{an}中,an+1=3an+4,且a1=1,求通项公式.
∵an+1=3an+4,
∴an+1+2=3(an+2).
令bn=an+2,∵b1=a1+2=3,
∴数列{bn}是首项为3,公比为3的等比数列,
则bn=3n,
∴an=3n-2.
法一
题型一 求数列的通项公式
[例1] (2)已知数列{an}中,an+1=3an+4,且a1=1,求通项公式.
∵an+1=3an+4, ①
∴an=3an-1+4(n≥2). ②
①-②,得an+1-an=3(an-an-1)(n≥2).
∵a2-a1=3+4-1=6,
∴数列{an+1-an}是首项为6,公比为3的等比数列,
即an+1-an=6×3n-1=2×3n,利用累加法得an=3n-2.
法二
方法总结
累加或
累乘法
直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适用于已知数列类型的题目.
已知Sn求an
若已知数列的前n项和Sn与an的关系,求数列{an}的通项an可用公式an= 求解.
形如an-an-1=f(n)(n≥2)的递推式,可用累加法求通项公式;形如=f(n)(n≥2)的递推式,可用累乘法求通项公式.
构造法
如an+1=Aan+B可构造{an+n}为等比数列,再求解得通项公式.
定义法
数列通项公式的求法
跟踪训练
1.已知数列{an}的前n项和Sn=2n-an,求数列的通项公式an.
由a1=S1=2-a1,得a1=1.
当n≥2时,an=Sn-Sn-1=2n-an-[2(n-1)-an-1]=-an+2+an-1,
所以an= an-1+1,即an-2= (an-1-2).
令bn=an-2,则bn= bn-1,且b1=1-2=-1,
于是数列{bn}是首项为-1,公比为的等比数列,
所以bn=-1×()n-1=-()n-1 ,故an=2- ()n-1.
题型二 等差、等比数列的基本运算
[例2] 等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式;
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
[例2] 等比数列{an}中,已知a1=2,a4=16.
(1) 求数列{an}的通项公式;
设{an}的公比为q,
a1=2,a4=16
16=2q3
q=2
an=2×2n-1=2n
[例2] 等比数列{an}中,已知a1=2,a4=16.
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
由(1)得a3=8,a5=32,则b3=8,b5=32.
设{bn}的公差为d,则有
所以bn=-16+12(n-1)=12n-28.
所以数列{bn}的前n项和Sn= =6n2-22n.
解得
在等差数列和等比数列的通项公式an与前n项和公式Sn中,共涉及五个量:a1,an,n,d(或q),Sn,其中a1和d(或q)为基本量,“知三求二”是指将已知条件转换成关于a1,d(q),an,Sn,n的方程组,利用方程的思想求出需要的量,当然在求解中若能运用等差(比)数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.
方法总结
跟踪训练
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
(2)记{an}的前n项和为Sn,求Sn的最小值.
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
∵{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列,
∴(a3+8)2=(a2+10)(a4+6),
∴(-2+2d)2=d(-4+3d),解得d=2,
∴an=a1+(n-1)d=-10+2n-2=2n-12.
2.设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(2)记{an}的前n项和为Sn,求Sn的最小值.
∴n=5或n=6时,Sn取最小值-30.
由a1=-10,d=2,得:
Sn=-10n+×2=n2-11n= ,
题型三 等差、等比数列的判定
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列;
(2)设cn= ,求证:{cn}是等差数列.
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列;
an+2=Sn+2-Sn+1=4an+1+2-4an-2=4an+1-4an.
=2.
因为S2=a1+a2=4a1+2,所以a2=5.
所以b1=a2-2a1=3.
所以数列{bn}是首项为3,公比为2的等比数列.
[例3] 数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(2)设cn= ,求证:{cn}是等差数列.
由(1)知bn=3·2n-1=an+1-2an,
所以=3.
所以cn+1-cn=3,且c1= =2,
所以数列{cn}是等差数列,公差为3,首项为2.
等差数列、等比数列的判断方法
(1)定义法
an+1-an=d(常数) {an}是等差数列;
=q(q为常数,q≠0) {an}是等比数列.
(2)中项公式法
2an+1=an+an+2 {an}是等差数列;
=an·an+2(an≠0) {an}是等比数列.
(3)通项公式法
an=kn+b(k,b是常数) {an}是等差数列;
an=c·qn(c,q为非零常数) {an}是等比数列.
(4)前n项和公式法
Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;
Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
跟踪训练
3.已知数列{an}满足a1=1,an+1=3an+1.
(1)证明是等比数列,并求{an}的通项公式;
(2)证明+ +…+ < .
3.已知数列{an}满足a1=1,an+1=3an+1.
(1)证明是等比数列,并求{an}的通项公式;
由an+1=3an+1得an+1+=3(an+ ).
因为a1+= ,
所以是首项为,公比为3的等比数列.
所以an+ = ,因此{an}的通项公式为an= .
3.已知数列{an}满足a1=1,an+1=3an+1.
(2)证明+ +…+ < .
由(1)知= .
因为当n≥1时,3n-1≥2×3n-1,所以≤ .
于是+ +…+ ≤1++…+ = (1- )< .
所以+ +…+ < .
题型四 等差、等比数列的性质
[例4] (1) (多选题)等差数列{an}的公差为d,前n项和为Sn,当首项a1和d变化时,a3+a8+a13是一个定值,则下列各数也为定值的有( )
A.a7 B.a8 C.S15 D.S16
由等差中项的性质可得a3+a8+a13=3a8为定值,
则a8为定值,S15= =15a8为定值,
但S16= =8不是定值.
BC
(2) (多选题)设等比数列{an}的公比为q,其前n项和为Sn,前n项积为Tn,并满足条件a1>1,a2019a2020>1, <0,下列结论正确的是( )
A.S2019
当q<0时,a2019a2020= q<0,不成立;
当q≥1时,a2019≥1,a2020>1, <0不成立;
故0<q<1,且a2019>1,0<a2020<1,故S2020>S2019,A正确;
a2019a2021-1= -1<0,故B正确;
T2019是数列{Tn}中的最大值,CD错误.
AB
(3)等比数列{an}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5=________.
由等比数列的性质知a1a5=a2a4= =4 a3=2,
5
log2a1+log2a2+log2a3+log2a4+log2a5
=log2(a1a2a3a4a5)
=log2
=5log22
=5.
(1)等差数列、等比数列公式和性质的灵活应用;
(2)对于计算解答题注意基本量及方程思想的运用;
(3)注重问题的转化,由非等差数列、非等比数列构造出新的等差数列或等比数列,以便利用相关公式和性质解题;
(4)当题目中出现多个数列时,既要纵向考察单一数列的项与项之间的关系,又要横向考察各数列之间的内在联系.
解决等差、等比数列有关问题的几点注意
方法总结
跟踪训练
4.(1)已知{an}为等比数列,且an>0,a2a4+2a3a5+a4a6=25,求a3+a5的值.
因为数列{an}为等比数列,
∴a2a4=,a4a6= ,
又∵a2a4+2a3a5+a4a6=25,
∴ +2a3a5+ =25,而an>0,
故a3+a5=5.
跟踪训练
4. (2)在等比数列{an}中,已知Sn=48,S2n=60,求S3n.
根据数列{an}为等比数列,
则Sn,S2n-Sn,S3n-S2n,…成等比数列,
即48,60-48,S3n-60,…成等比数列,
∴48×(S3n-60)=122,
解得S3n=63.
题型五 数列求和
1.若数列{cn}是公差为d的等差数列,数列{bn}是公比为q(q≠1)的等比数列,且an=cn+bn,如何求数列{an}的前n项和?
[探究问题]
[提示]
数列{an}的前n项和等于数列{cn}和{bn}的前n项和的和.
2.有些数列单独看求和困难,但相邻项结合后会变成熟悉的等差数列、等比数列求和.试用此种方法求和:
12-22+32-42+…+992-1002.
[探究问题]
[提示]
12-22+32-42+…+992-1002=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2+3+4+…+99+100)=-5050.
3.我们知道= -,试用此公式求和: + +…+ .
[提示] 由= -得 + +…+
=1-+ - +…+ - =1- = .
[探究问题]
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和.
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1) 求an;
当n≥2时,an=Sn-Sn-1=k(cn-cn-1),
则a6=k(c6-c5),a3=k(c3-c2),= =c3=8,
∴c=2.
∵a2=4,即k(c2-c1)=4,
∴an=2n.
当n=1时,a1=S1=2.
综上所述,an=2n(n∈N*).
解得k=2,
[例5] 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(2)求数列{nan}的前n项和.
nan=n·2n,
则Tn=2+2·22+3·23+…+n·2n,
2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,
两式作差得-Tn=2+22+23+…+2n-n·2n+1,
∴Tn=2+(n-1)·2n+1.
多维探究
变式1 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
求数列{n+an}的前n项和Tn .
Tn=1+2+2+22+3+23+…+n+2n
=(1+2+3+…+n)+(2+22+…+2n)
= +
=2n+1-2+
变式2 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3. 求数列的前n项和Tn.
Tn= + + +…+ , ①
Tn= + +…+ +, ②
Tn= + + +…+ - = =1--,
∴Tn=2- - =2- .
①-②得:
变式3 已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3. 设Sn是数列{an}的前n项和,bn= ,求数列{bn}的前n项和Tn.
由(1)知an=2n,
∴Sn= = =2n+1-2.
因为bn= = = -,
所以Tn=b1+b2+…+bn=(-)+(-)+…+(-)= - = - = .
数列求和问题一般转化为等差数列或等比数列的前n项和问题或已知公式的数列求和,不能转化的再根据数列通项公式的特点选择恰当的方法求解.一般常见的求和方法有:
(1)公式法:利用等差数列或等比数列前n项和公式.
(2)分组求和法:把一个数列分成几个可以直接求和的数列.
(3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和.
(4)错位相减法:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和.
(5)倒序相加法:例如,等差数列前n项和公式的推导.
方法总结
