人教版(2019)数学选择性必修二 第五章一元函数的导数及其应用 章末复习课件(共31张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修二 第五章一元函数的导数及其应用 章末复习课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:16:22 | ||
图片预览










文档简介
(共31张PPT)
第五章 一元函数的导数及其应用
高二选择性必修二
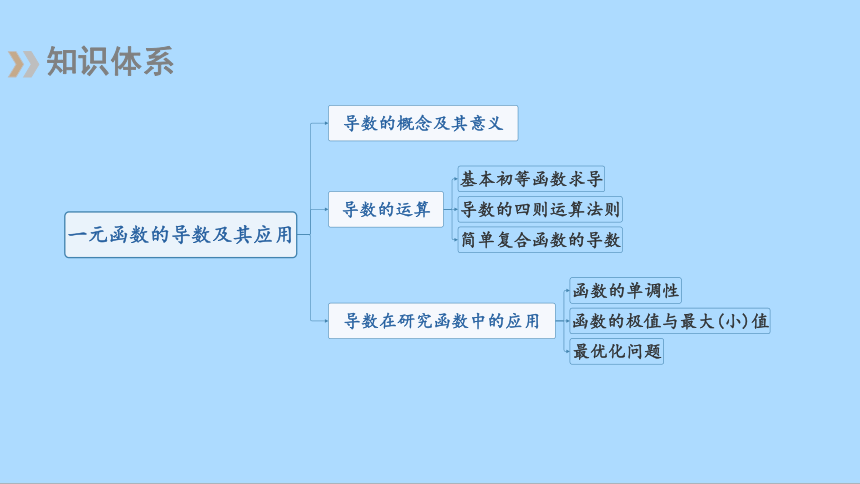
知识体系
导数的概念及其意义
导数的运算
导数在研究函数中的应用
基本初等函数求导
导数的四则运算法则
简单复合函数的导数
函数的单调性
函数的极值与最大(小)值
最优化问题
一元函数的导数及其应用
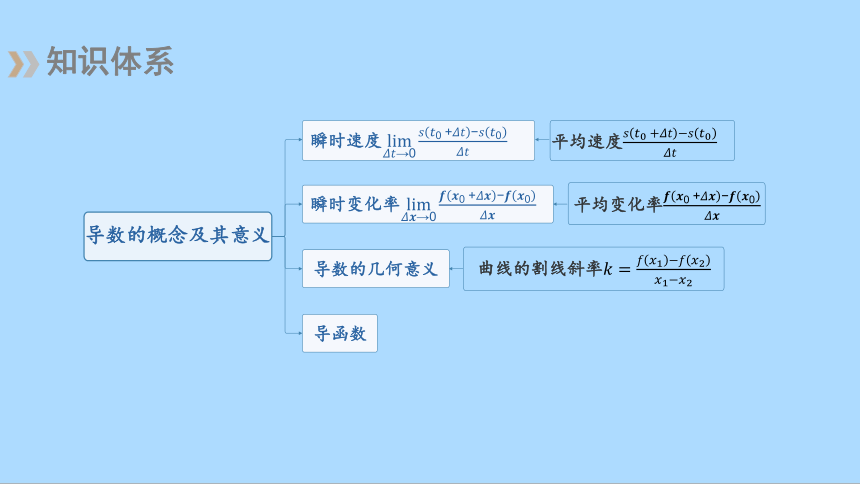
知识体系
瞬时速度
瞬时变化率
导数的几何意义
导函数
平均速度
平均变化率
曲线的割线斜率
导数的概念及其意义
题型突破
典例深度剖析 重点多维探究
题型一 导数的概念及几何意义的应用
[例1] 已知a∈R,设函数f(x)=ax-ln x的图象在点(1,f(1))处的切线为l,则l在y轴上的截距为________.
由题意可知f ′(x)=a-,
所以f ′(1)=a-1,
因为f(1)=a,所以切点坐标为(1,a),
所以切线l的方程为y-a=(a-1)(x-1),
即y=(a-1)x+1.
令x=0,得y=1,即直线l在y轴上的截距为1.
1
曲线与直线相切并不一定只有一个公共点
利用导数的几何意义解决切线问题的两种情况
①若已知点是切点,则在该点处的切线斜率就是该点处的导数.
②如果已知点不是切点,则应先出切点,再借助两点连线的斜率公式进行求解.
例如,y=x3在(1,1)处的切线l与y=x3的图象还有一个交点(-2,-8).
方法总结
跟踪训练
1.曲线y=在点(-1,-1)处的切线方程为( )
A.y=2x+1 B.y=2x-1
C.y=-2x-3 D.y=-2x-2
y′= =
k=y′|x=-1= =2
切线方程为:y+1=2(x+1),即y=2x+1
A
2.已知曲线y=x3-1与曲线y=3-x2在x=x0处的切线互相垂直,则x0的值为( )
A. B. C. D.
y=x3-1 y′=3x2,
y=3-x2 y′=-x,
由题意得3·(-x0)=-1,
解得=,即x0== ,
D
题型二 导数与函数的单调性
[例2] 已知函数f(x)=ln x+ax2+(2a+1)x.讨论f(x)的单调性.
f(x)的定义域为(0,+∞),f ′(x)=+2ax+2a+1=.
若a≥0,则当x∈(0,+∞)时,f ′(x)>0,
故f(x)在(0,+∞)单调递增.
若a<0,则当x∈时,f ′(x)>0;
当x∈ (,+∞)时,f ′(x)<0,
故f(x)在上单调递增,在(,+∞)上单调递减.
(3)解不等式f ′(x)>0,得到函数f(x)的递增区间;
解不等式f ′(x)<0,得到函数f(x)的递减区间.
求函数的单调区间的方法步骤
求函数单调区间一定要先确定函数定义域,往往因忽视函数定义域而导致错误.
(1)确定函数f(x)的定义域.
(2)计算函数f(x)的导数f ′(x).
方法总结
易错提醒
跟踪训练
1.函数f(x)=2x2-ln x的单调递增区间是( )
A. B. 和
C. D. 和
f ′(x)=4x-= ,且x>0,
由f ′(x)>0,即4x2-1>0,解得x>.
C
2.已知函数f(x)=-x2+2x-aex.
(1)若a=1,求f(x)在x=1处的切线方程;
(2)若f(x)在R上是增函数,求实数a的取值范围.
跟踪训练
2.已知函数f(x)=-x2+2x-aex.
(1)若a=1,求f(x)在x=1处的切线方程;
f ′(x)=-x+2-ex,f ′(1)=-1+2-e=1-e,
当a=1时,f(x)=-x2+2x-ex,
则f(1)=-×12+2×1-e=-e,
故曲线y=f(x)在x=1处的切线方程为y-(-e)=(1-e)(x-1),即y=(1-e)x+.
2.已知函数f(x)=-x2+2x-aex.
(2)若f(x)在R上是增函数,求实数a的取值范围.
∵f(x)在R上是增函数,∴f ′(x)≥0在R上恒成立,
∵f(x)=-x2+2x-aex,
∴f ′(x)=-x+2-aex,
于是有不等式-x+2-aex≥0在R上恒成立,
即a≤ 在R上恒成立,
令g(x)= ,则g′(x)= ,
2.已知函数f(x)=-x2+2x-aex.
(2)若f(x)在R上是增函数,求实数a的取值范围.
令g′(x)=0,解得x=3,列表如下:
x (-∞,3) 3 (3,+∞)
g′(x) - 0 +
g(x)
故函数g(x)在x=3处取得极小值,亦即最小值,
即g(x)min=-,所以a≤- ,
即实数a的取值范围是(-∞, ).
题型三 导数与函数的极值、最值
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间上的最大值和最小值.
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
因为f(x)=excos x-x,
所以f ′(x)=ex(cos x-sin x)-1,f ′(0)=0.
又因为f(0)=1,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(2)求函数f(x)在区间上的最大值和最小值.
设h(x)=ex(cos x-sin x)-1,
则h′(x)=ex(cos x-sin x-sin x-cos x)=-2exsin x.
当x∈()时,h′(x)<0,所以h(x)在区间上单调递减.
所以对任意x∈有h(x)<h(0)=0,即f ′(x)<0.
所以函数f(x)在区间上单调递减.
因此f(x)在区间上的最大值为f(0)=1,最小值为f()=-.
(1)确定函数的定义区间,求导数f ′(x).
(2)求方程f ′(x)=0的根.
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f ′(x)在方程根左右的值的符号,
如果左正右负,那么f(x)在这个根处取得极大值;
如果左负右正,那么f(x)在这个根处取得极小值;
如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值.
方法总结
求函数的极值的方法
(1) 求f(x)在(a,b)内的极值.
(2) 将f(x)的各极值与f(a),f(b)比较得出函数f(x)在[a,b]上的最值.
求函数的最值的方法
方法总结
跟踪训练
1.函数f(x)=1+3x-x3( )
A.有极小值,无极大值 B.无极小值,有极大值
C.无极小值,无极大值 D.有极小值,有极大值
f ′(x)=-3x2+3,由f ′(x)=0,得x=±1.
当x∈(-1,1)时,f ′(x)>0,∴f(x)的单调增区间为(-1,1);
同理,f(x)的单调减区间为(-∞,-1)和(1,+∞).
∴当x=-1时,函数有极小值-1,
当x=1时,函数有极大值3.
D
2.已知函数f(x)=(x≥1),
(1)试判断函数f(x)的单调性,并说明理由;
(2)若f(x)≥ 恒成立,求实数k的取值范围.
跟踪训练
2.已知函数f(x)=(x≥1),
(1)试判断函数f(x)的单调性,并说明理由;
f ′(x)=-
x≥1
ln x≥0
f ′(x)≤0
函数f(x)在[1,+∞)上单调递减
2.已知函数f(x)=(x≥1),
(2)若f(x)≥ 恒成立,求实数k的取值范围.
∵x≥1,∴f(x)≥ ≥k,
∵x≥1,则h′(x)≥0,∴h(x)在[1,+∞)上单调递增.
∴[h(x)]min=h(1)=1>0,从而g′(x)>0,故g(x)在[1,+∞)上单调递增,
∴[g(x)]min=g(1)=2,∴k≤2.
故实数k的取值范围为(-∞, 2].
令g(x)=,∴g′(x)= .
再令h(x)=x-ln x,则h′(x)=1- .
题型四 生活中的优化问题
[例4] 某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π 元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域.
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
[例4] (1)将V表示成r的函数V(r),并求该函数的定义域.
因为蓄水池侧面的总成本为100·2πrh=200πrh(元),底面的总成本为160πr2元,
所以蓄水池的总成本为(200πrh+160πr2)元.
又据题意知200πrh+160πr2=12000π,
所以h= (300-4r2),
从而V(r)=πr2h= (300r-4r3).
因为r>0,又由h>0可得r<5,
故函数V(r)的定义域为(0, 5).
[例4] (2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
因为V(r)= (300r-4r3),所以V ′(r)= (300-12r2).
令V ′(r)=0,解得r1=5,r2=-5(因r2=-5不在定义域内,舍去).
当r∈(0,5)时,V′(r)>0,故V(r)在(0,5)上为增函数;
当r∈(5,5)时,V′(r)<0,故V(r)在(5,5)上为减函数.
由此可知,V(r)在r=5处取得最大值,此时h=8.
即当r=5,h=8时,该蓄水池的体积最大.
(1)分析实际问题中各个量之间的关系,正确设定所求最大或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),根据实际问题确定y=f(x)的定义域.
利用导数求实际问题的最大(小)值的一般方法
方法总结
(2)求方程f ′(x)=0的所有实数根.
(3)比较导函数在各个根和区间端点处的函数值的大小,根据实际问题的意义确定函数的最大值或最小值.
跟踪训练
1.书店预计一年内要销售某种书15万册,欲分几次订货,如果每次订货要付手续费30元,每千册书存放一年要耗库存费40元,并假设该书均匀投放市场,问此书店分________次进货、每次进__________册,可使所付的手续费与库存费之和最少.
1.书店预计一年内要销售某种书15万册,欲分几次订货,如果每次订货要付手续费30元,每千册书存放一年要耗库存费40元,并假设该书均匀投放市场,问此书店分________次进货、每次进__________册,可使所付的手续费与库存费之和最少.
设每次进书x千册(0<x<150),手续费与库存费之和为y元,由于该书均匀投放市场,则平均库存量为批量一半,即,故有y= ×30+×40,y′=-+20= ,
∴当0<x<15时,y′<0,当15<x<150时,y′>0.
故当x=15时,y取得最小值,此时进货次数为=10(次).
即该书店分10次进货,每次进15000册书,所付手续费与库存费之和最少.
10
15000
2.一艘轮船在航行时的燃料费和它的速度的立方成正比,已知速度为每小时10千米时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每千米的费用总和最小?
设轮船速度为x(x>0)千米/时的燃料费用为Q元,则Q=kx3,
由6=k×103,可得k=. ∴Q= x3.
∴总费用y=(x3+96)· =x2+.
∵y′=-.
∴当x=20时,y取得最小值,
∴此轮船以20千米/时的速度行驶每千米的费用总和最小.
令y′=0,得x=20.
∴当x∈(0,20)时,y′<0,此时函数单调递减,
当x∈(20,+∞)时,y′>0,此时函数单调递增.
第五章 一元函数的导数及其应用
高二选择性必修二
知识体系
导数的概念及其意义
导数的运算
导数在研究函数中的应用
基本初等函数求导
导数的四则运算法则
简单复合函数的导数
函数的单调性
函数的极值与最大(小)值
最优化问题
一元函数的导数及其应用
知识体系
瞬时速度
瞬时变化率
导数的几何意义
导函数
平均速度
平均变化率
曲线的割线斜率
导数的概念及其意义
题型突破
典例深度剖析 重点多维探究
题型一 导数的概念及几何意义的应用
[例1] 已知a∈R,设函数f(x)=ax-ln x的图象在点(1,f(1))处的切线为l,则l在y轴上的截距为________.
由题意可知f ′(x)=a-,
所以f ′(1)=a-1,
因为f(1)=a,所以切点坐标为(1,a),
所以切线l的方程为y-a=(a-1)(x-1),
即y=(a-1)x+1.
令x=0,得y=1,即直线l在y轴上的截距为1.
1
曲线与直线相切并不一定只有一个公共点
利用导数的几何意义解决切线问题的两种情况
①若已知点是切点,则在该点处的切线斜率就是该点处的导数.
②如果已知点不是切点,则应先出切点,再借助两点连线的斜率公式进行求解.
例如,y=x3在(1,1)处的切线l与y=x3的图象还有一个交点(-2,-8).
方法总结
跟踪训练
1.曲线y=在点(-1,-1)处的切线方程为( )
A.y=2x+1 B.y=2x-1
C.y=-2x-3 D.y=-2x-2
y′= =
k=y′|x=-1= =2
切线方程为:y+1=2(x+1),即y=2x+1
A
2.已知曲线y=x3-1与曲线y=3-x2在x=x0处的切线互相垂直,则x0的值为( )
A. B. C. D.
y=x3-1 y′=3x2,
y=3-x2 y′=-x,
由题意得3·(-x0)=-1,
解得=,即x0== ,
D
题型二 导数与函数的单调性
[例2] 已知函数f(x)=ln x+ax2+(2a+1)x.讨论f(x)的单调性.
f(x)的定义域为(0,+∞),f ′(x)=+2ax+2a+1=.
若a≥0,则当x∈(0,+∞)时,f ′(x)>0,
故f(x)在(0,+∞)单调递增.
若a<0,则当x∈时,f ′(x)>0;
当x∈ (,+∞)时,f ′(x)<0,
故f(x)在上单调递增,在(,+∞)上单调递减.
(3)解不等式f ′(x)>0,得到函数f(x)的递增区间;
解不等式f ′(x)<0,得到函数f(x)的递减区间.
求函数的单调区间的方法步骤
求函数单调区间一定要先确定函数定义域,往往因忽视函数定义域而导致错误.
(1)确定函数f(x)的定义域.
(2)计算函数f(x)的导数f ′(x).
方法总结
易错提醒
跟踪训练
1.函数f(x)=2x2-ln x的单调递增区间是( )
A. B. 和
C. D. 和
f ′(x)=4x-= ,且x>0,
由f ′(x)>0,即4x2-1>0,解得x>.
C
2.已知函数f(x)=-x2+2x-aex.
(1)若a=1,求f(x)在x=1处的切线方程;
(2)若f(x)在R上是增函数,求实数a的取值范围.
跟踪训练
2.已知函数f(x)=-x2+2x-aex.
(1)若a=1,求f(x)在x=1处的切线方程;
f ′(x)=-x+2-ex,f ′(1)=-1+2-e=1-e,
当a=1时,f(x)=-x2+2x-ex,
则f(1)=-×12+2×1-e=-e,
故曲线y=f(x)在x=1处的切线方程为y-(-e)=(1-e)(x-1),即y=(1-e)x+.
2.已知函数f(x)=-x2+2x-aex.
(2)若f(x)在R上是增函数,求实数a的取值范围.
∵f(x)在R上是增函数,∴f ′(x)≥0在R上恒成立,
∵f(x)=-x2+2x-aex,
∴f ′(x)=-x+2-aex,
于是有不等式-x+2-aex≥0在R上恒成立,
即a≤ 在R上恒成立,
令g(x)= ,则g′(x)= ,
2.已知函数f(x)=-x2+2x-aex.
(2)若f(x)在R上是增函数,求实数a的取值范围.
令g′(x)=0,解得x=3,列表如下:
x (-∞,3) 3 (3,+∞)
g′(x) - 0 +
g(x)
故函数g(x)在x=3处取得极小值,亦即最小值,
即g(x)min=-,所以a≤- ,
即实数a的取值范围是(-∞, ).
题型三 导数与函数的极值、最值
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间上的最大值和最小值.
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
因为f(x)=excos x-x,
所以f ′(x)=ex(cos x-sin x)-1,f ′(0)=0.
又因为f(0)=1,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
[例3] (北京高考)已知函数f(x)=ex cos x-x.
(2)求函数f(x)在区间上的最大值和最小值.
设h(x)=ex(cos x-sin x)-1,
则h′(x)=ex(cos x-sin x-sin x-cos x)=-2exsin x.
当x∈()时,h′(x)<0,所以h(x)在区间上单调递减.
所以对任意x∈有h(x)<h(0)=0,即f ′(x)<0.
所以函数f(x)在区间上单调递减.
因此f(x)在区间上的最大值为f(0)=1,最小值为f()=-.
(1)确定函数的定义区间,求导数f ′(x).
(2)求方程f ′(x)=0的根.
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f ′(x)在方程根左右的值的符号,
如果左正右负,那么f(x)在这个根处取得极大值;
如果左负右正,那么f(x)在这个根处取得极小值;
如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值.
方法总结
求函数的极值的方法
(1) 求f(x)在(a,b)内的极值.
(2) 将f(x)的各极值与f(a),f(b)比较得出函数f(x)在[a,b]上的最值.
求函数的最值的方法
方法总结
跟踪训练
1.函数f(x)=1+3x-x3( )
A.有极小值,无极大值 B.无极小值,有极大值
C.无极小值,无极大值 D.有极小值,有极大值
f ′(x)=-3x2+3,由f ′(x)=0,得x=±1.
当x∈(-1,1)时,f ′(x)>0,∴f(x)的单调增区间为(-1,1);
同理,f(x)的单调减区间为(-∞,-1)和(1,+∞).
∴当x=-1时,函数有极小值-1,
当x=1时,函数有极大值3.
D
2.已知函数f(x)=(x≥1),
(1)试判断函数f(x)的单调性,并说明理由;
(2)若f(x)≥ 恒成立,求实数k的取值范围.
跟踪训练
2.已知函数f(x)=(x≥1),
(1)试判断函数f(x)的单调性,并说明理由;
f ′(x)=-
x≥1
ln x≥0
f ′(x)≤0
函数f(x)在[1,+∞)上单调递减
2.已知函数f(x)=(x≥1),
(2)若f(x)≥ 恒成立,求实数k的取值范围.
∵x≥1,∴f(x)≥ ≥k,
∵x≥1,则h′(x)≥0,∴h(x)在[1,+∞)上单调递增.
∴[h(x)]min=h(1)=1>0,从而g′(x)>0,故g(x)在[1,+∞)上单调递增,
∴[g(x)]min=g(1)=2,∴k≤2.
故实数k的取值范围为(-∞, 2].
令g(x)=,∴g′(x)= .
再令h(x)=x-ln x,则h′(x)=1- .
题型四 生活中的优化问题
[例4] 某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π 元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域.
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
[例4] (1)将V表示成r的函数V(r),并求该函数的定义域.
因为蓄水池侧面的总成本为100·2πrh=200πrh(元),底面的总成本为160πr2元,
所以蓄水池的总成本为(200πrh+160πr2)元.
又据题意知200πrh+160πr2=12000π,
所以h= (300-4r2),
从而V(r)=πr2h= (300r-4r3).
因为r>0,又由h>0可得r<5,
故函数V(r)的定义域为(0, 5).
[例4] (2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
因为V(r)= (300r-4r3),所以V ′(r)= (300-12r2).
令V ′(r)=0,解得r1=5,r2=-5(因r2=-5不在定义域内,舍去).
当r∈(0,5)时,V′(r)>0,故V(r)在(0,5)上为增函数;
当r∈(5,5)时,V′(r)<0,故V(r)在(5,5)上为减函数.
由此可知,V(r)在r=5处取得最大值,此时h=8.
即当r=5,h=8时,该蓄水池的体积最大.
(1)分析实际问题中各个量之间的关系,正确设定所求最大或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),根据实际问题确定y=f(x)的定义域.
利用导数求实际问题的最大(小)值的一般方法
方法总结
(2)求方程f ′(x)=0的所有实数根.
(3)比较导函数在各个根和区间端点处的函数值的大小,根据实际问题的意义确定函数的最大值或最小值.
跟踪训练
1.书店预计一年内要销售某种书15万册,欲分几次订货,如果每次订货要付手续费30元,每千册书存放一年要耗库存费40元,并假设该书均匀投放市场,问此书店分________次进货、每次进__________册,可使所付的手续费与库存费之和最少.
1.书店预计一年内要销售某种书15万册,欲分几次订货,如果每次订货要付手续费30元,每千册书存放一年要耗库存费40元,并假设该书均匀投放市场,问此书店分________次进货、每次进__________册,可使所付的手续费与库存费之和最少.
设每次进书x千册(0<x<150),手续费与库存费之和为y元,由于该书均匀投放市场,则平均库存量为批量一半,即,故有y= ×30+×40,y′=-+20= ,
∴当0<x<15时,y′<0,当15<x<150时,y′>0.
故当x=15时,y取得最小值,此时进货次数为=10(次).
即该书店分10次进货,每次进15000册书,所付手续费与库存费之和最少.
10
15000
2.一艘轮船在航行时的燃料费和它的速度的立方成正比,已知速度为每小时10千米时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每千米的费用总和最小?
设轮船速度为x(x>0)千米/时的燃料费用为Q元,则Q=kx3,
由6=k×103,可得k=. ∴Q= x3.
∴总费用y=(x3+96)· =x2+.
∵y′=-.
∴当x=20时,y取得最小值,
∴此轮船以20千米/时的速度行驶每千米的费用总和最小.
令y′=0,得x=20.
∴当x∈(0,20)时,y′<0,此时函数单调递减,
当x∈(20,+∞)时,y′>0,此时函数单调递增.
