28.1锐角三角函数(1)[下学期]
文档属性
| 名称 | 28.1锐角三角函数(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-03 00:00:00 | ||
图片预览




文档简介
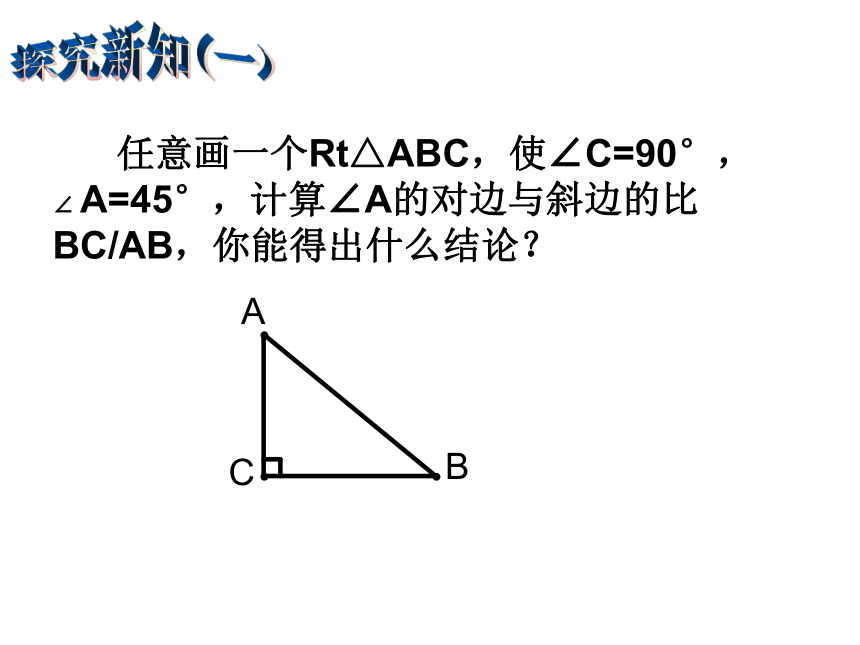
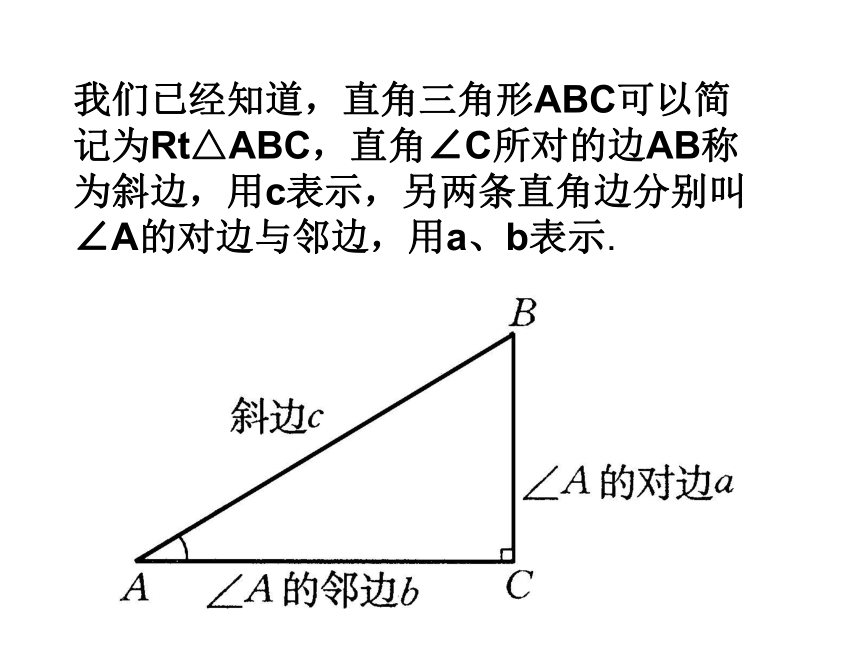
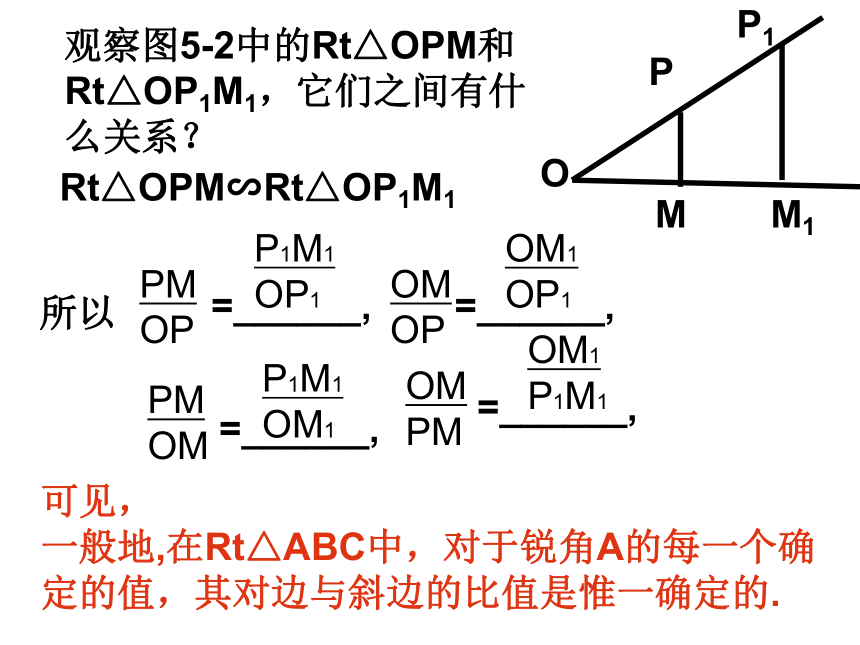
课件17张PPT。28.1 锐角三角函数(1)ABC“斜而未倒”BC=5.2mAB=54.5mα探究新知(一) 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管? 请你用几何图形和数学语言来表示。 在直角三角形中, 30°角所对的直角边等于斜边的一半。这个问题中若高度变为50m,则要多长的水管?探究新知(一) 任意画一个Rt△ABC,使∠C=90°, ∠ A=45°,计算∠A的对边与斜边的比BC/AB,你能得出什么结论?我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示. 观察图5-2中的Rt△OPM和Rt△OP1M1,它们之间有什么关系?Rt△OPM∽Rt△OP1M1P1M1
OP1OM
OPOM1
OP1PM
OMOM
PMP1M1
OM1=______,=______,=______,OM1
P1M1=______,OPM1P1M结论 在Rt△ABC中, ∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine)。记作sinA,即(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积
(3) sinA 是一个比值 (4)sinA 没有单位应用新知例1、如图,在Rt△ABC中, ∠C=90°,求sinA和sinB的值。练习:P79-练习例2、已知锐角α的始边在x轴的正半轴上,
(顶点在原点)终边上一点P的坐标为(2, y),
sinα= 则y的值.(2,y)Msinα= 解:过P作OM⊥x轴于M,则OM=2,PM=y由勾股定理得OP=解得y=±∵y﹥0,∴y=应用新知例3、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。应用新知在平面直角坐标系中,有一条直线l:y=5/12x,l与x轴的正半轴的夹角为α,求sinα的值。成果检测练习:1.下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。2.上题中如果CD=5,AC=10,
则sin∠ACD=________
sin ∠DCB=________ 3. 在Rt△ABC中,∠C=Rt∠,BC:AC=1:2,则sinA= 。4.如图示, 在Rt△ABC中,∠B=Rt∠,b= c= ,则sin(90°-A)= 。5. 在Rt△ABC中,∠C=Rt∠,若sinA= ,则∠A= . ∠B= .
CBAbac中考链接:在△ABC中,∠B=90o ,BC=3,AB=4,则sinA=_____ sinC=______
(2003年北京 ) 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?用一用三角函数符号最早的使用1949年至今,由于受前苏联教材的影响,我国数学书籍中“cot”改为“ctg”,“tan”改为“tg”,其余四个符号均未变。这就是为什么我国市场上流行的进口函数计算器上有“tan”而无“tg”按键的缘故。小资料sine(正弦)一词始于阿拉伯人雷基奥蒙坦。他是十五世纪西欧数学界的领导
人物,他于1464年完成的著作《论各种三角形》,1533年开始发行,这是一
本纯三角学的书,使三角学脱离天文学,独立成为一门数学分科。Cosine(余弦)及cotangent(余切)为英国人根日尔首先使用,最早在1620年伦敦出版的他所著的《炮兵测量学》中出现。Secant(正割)及tangent(正切)为丹麦数学家托马斯·劳克首创,最早见于
他的《圆几何学》一书中。Cosecant(余割)一词为锐梯卡斯所创。最早见于他1596年出版的《宫廷乐章》一书。1626年,阿尔贝特·格洛德最早推出简写的三角符号:“sin” ,“tan” ,“sec”.
1675年,英国人奥屈特最早推出余下的简写三角符号:“cos”,“cot”,“csc”。便直到1748年,经过数学家欧拉的引用后,才逐渐通用起来。再见
OP1OM
OPOM1
OP1PM
OMOM
PMP1M1
OM1=______,=______,=______,OM1
P1M1=______,OPM1P1M结论 在Rt△ABC中, ∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine)。记作sinA,即(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积
(3) sinA 是一个比值 (4)sinA 没有单位应用新知例1、如图,在Rt△ABC中, ∠C=90°,求sinA和sinB的值。练习:P79-练习例2、已知锐角α的始边在x轴的正半轴上,
(顶点在原点)终边上一点P的坐标为(2, y),
sinα= 则y的值.(2,y)Msinα= 解:过P作OM⊥x轴于M,则OM=2,PM=y由勾股定理得OP=解得y=±∵y﹥0,∴y=应用新知例3、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。应用新知在平面直角坐标系中,有一条直线l:y=5/12x,l与x轴的正半轴的夹角为α,求sinα的值。成果检测练习:1.下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。2.上题中如果CD=5,AC=10,
则sin∠ACD=________
sin ∠DCB=________ 3. 在Rt△ABC中,∠C=Rt∠,BC:AC=1:2,则sinA= 。4.如图示, 在Rt△ABC中,∠B=Rt∠,b= c= ,则sin(90°-A)= 。5. 在Rt△ABC中,∠C=Rt∠,若sinA= ,则∠A= . ∠B= .
CBAbac中考链接:在△ABC中,∠B=90o ,BC=3,AB=4,则sinA=_____ sinC=______
(2003年北京 ) 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?用一用三角函数符号最早的使用1949年至今,由于受前苏联教材的影响,我国数学书籍中“cot”改为“ctg”,“tan”改为“tg”,其余四个符号均未变。这就是为什么我国市场上流行的进口函数计算器上有“tan”而无“tg”按键的缘故。小资料sine(正弦)一词始于阿拉伯人雷基奥蒙坦。他是十五世纪西欧数学界的领导
人物,他于1464年完成的著作《论各种三角形》,1533年开始发行,这是一
本纯三角学的书,使三角学脱离天文学,独立成为一门数学分科。Cosine(余弦)及cotangent(余切)为英国人根日尔首先使用,最早在1620年伦敦出版的他所著的《炮兵测量学》中出现。Secant(正割)及tangent(正切)为丹麦数学家托马斯·劳克首创,最早见于
他的《圆几何学》一书中。Cosecant(余割)一词为锐梯卡斯所创。最早见于他1596年出版的《宫廷乐章》一书。1626年,阿尔贝特·格洛德最早推出简写的三角符号:“sin” ,“tan” ,“sec”.
1675年,英国人奥屈特最早推出余下的简写三角符号:“cos”,“cot”,“csc”。便直到1748年,经过数学家欧拉的引用后,才逐渐通用起来。再见
