28.1锐角三角函数(2)[下学期]
文档属性
| 名称 | 28.1锐角三角函数(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-12 11:23:00 | ||
图片预览


文档简介
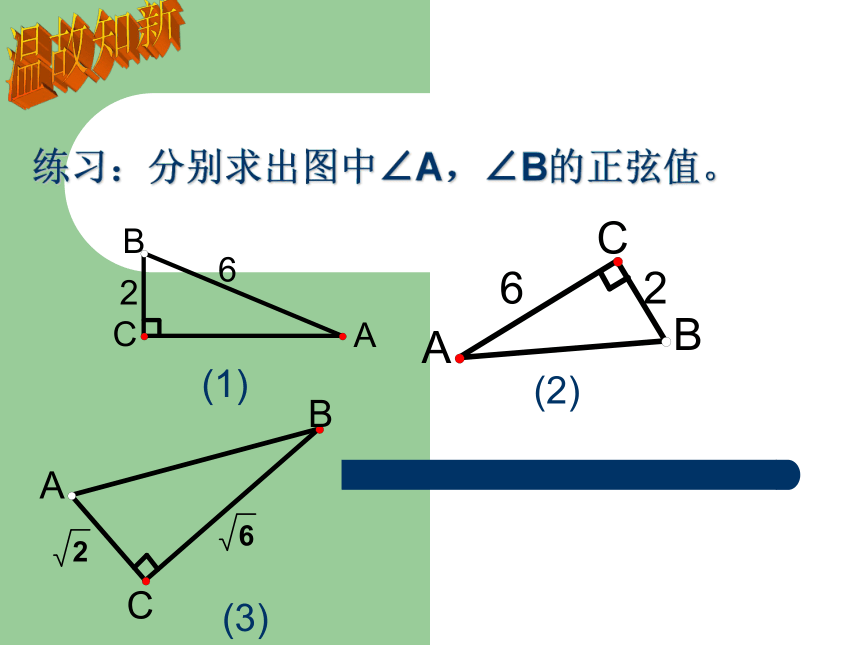
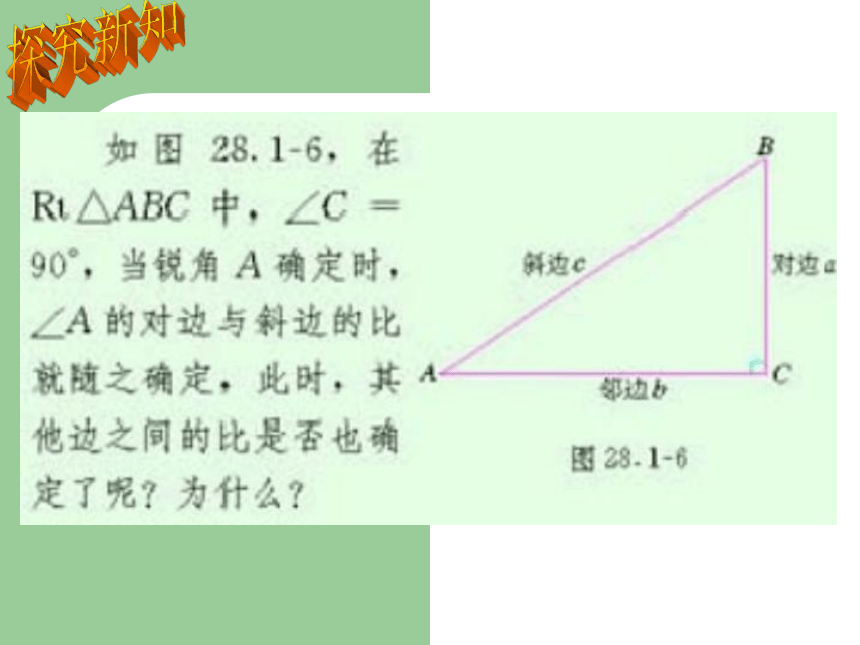
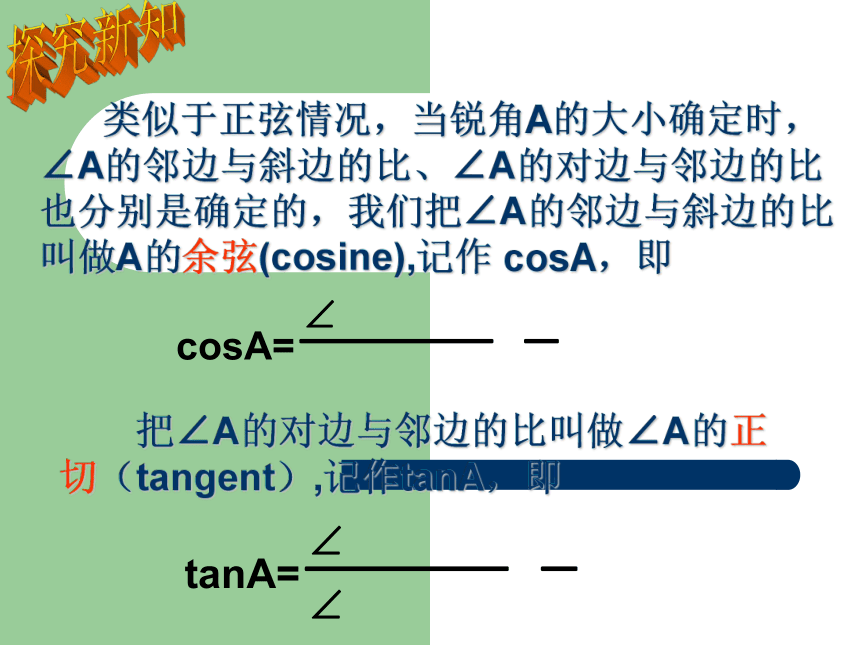
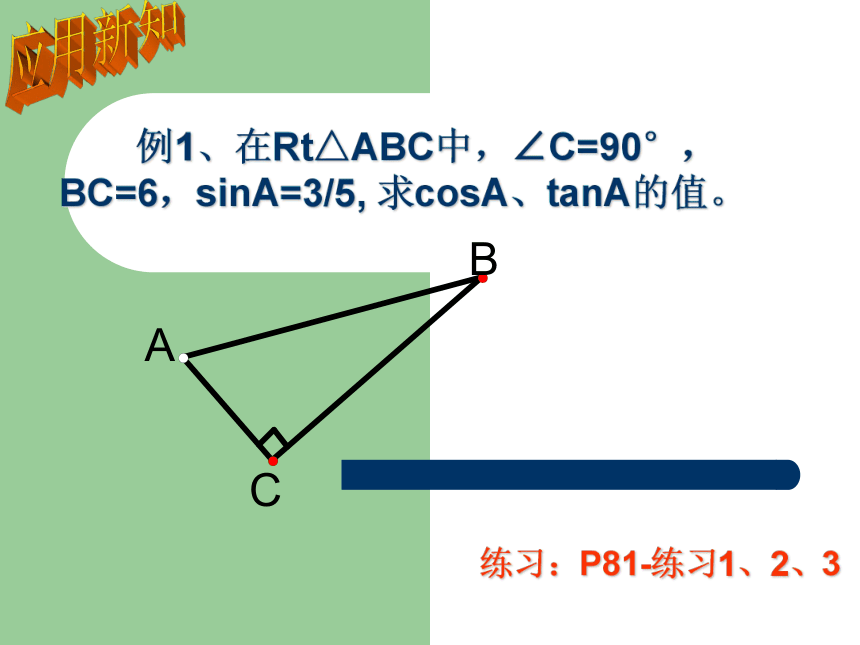
课件12张PPT。28.1锐角三角函数2温故知新练习:分别求出图中∠A,∠B的正弦值。(1)(3)(2)探究新知探究新知 类似于正弦情况,当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的,我们把∠A的邻边与斜边的比叫做A的余弦(cosine),记作 cosA,即 把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即探究新知 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。 对于锐角A的每一个确定的值,sinA有唯一的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。应用新知 例1、在Rt△ABC中,∠C=90°,BC=6,sinA=3/5, 求cosA、tanA的值。练习:P81-练习1、2、3锐角三角函数三、特殊角三角函数值11角度
逐渐
增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大余切值如何变化?余切值逐渐减小锐角A的正弦值、余弦值有无变化范围?0< sinA<1
0终边上一点P的坐标为(x, y),它到原点的距离为r
求角α的四个三角函数值。成果推广sinα= ,
cosα= ,
tanα= ,
cotα= .M 操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗?探索新知30° 利用正弦函数,余弦函数的定义说明: sin2A+cos2A=1思考:再见
逐渐
增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大余切值如何变化?余切值逐渐减小锐角A的正弦值、余弦值有无变化范围?0< sinA<1
0
求角α的四个三角函数值。成果推广sinα= ,
cosα= ,
tanα= ,
cotα= .M 操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗?探索新知30° 利用正弦函数,余弦函数的定义说明: sin2A+cos2A=1思考:再见
