人教A版选择性必修一 1.1.2 空间向量的数量积运算 课件(25张PPT)
文档属性
| 名称 | 人教A版选择性必修一 1.1.2 空间向量的数量积运算 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
1.1.2 空间向量的数量积运算
新知探究
2
新知引入
1
教学目标:
(1)通过类比的思想,理解和掌握空间向量数量积的定义、性质以及运算律;(2)掌握空间向量投影及投影向量,理解空间向量数量积的几何意义;
(3)基本掌握空间向量数量积运算解决空间距离、夹角问题.进一步体会空间向量解决立体几何问题的思想与方法.
教学重点:空间向量的数量积极概念以及空间向量投影
教学难点:空间向量的投影以及数量积的分配律;用空间向量表示所涉及的几何元素.
平面向量及其线性运算
空间向量及其线性运算
推 广
平面向量的数量积运算
空间向量的数量积运算
推 广
新知引入
1
思考 学习平面向量时,是如何研究它的数量积运算的?
夹角
数量积的定义
运算律
应用
新知引入
1
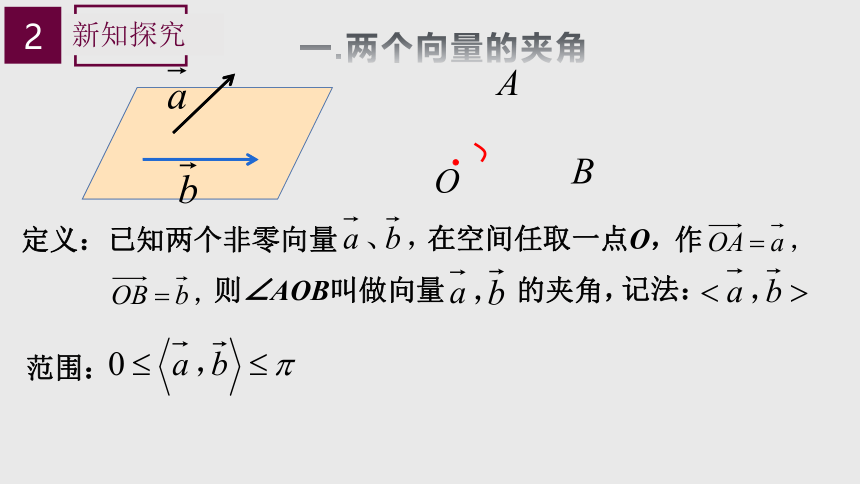
一.两个向量的夹角
定义:已知两个非零向量
在空间任取一点O,
则∠AOB叫做向量
的夹角,
记法:
作
范围:
新知探究
2
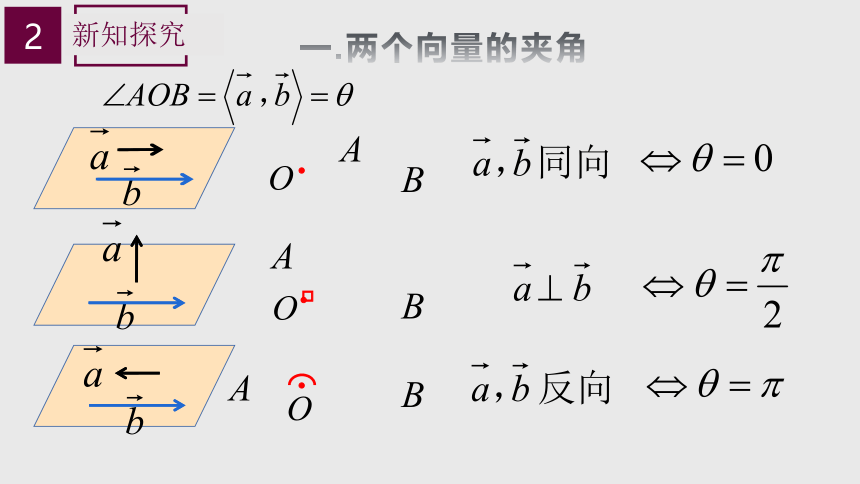
一.两个向量的夹角
新知探究
2
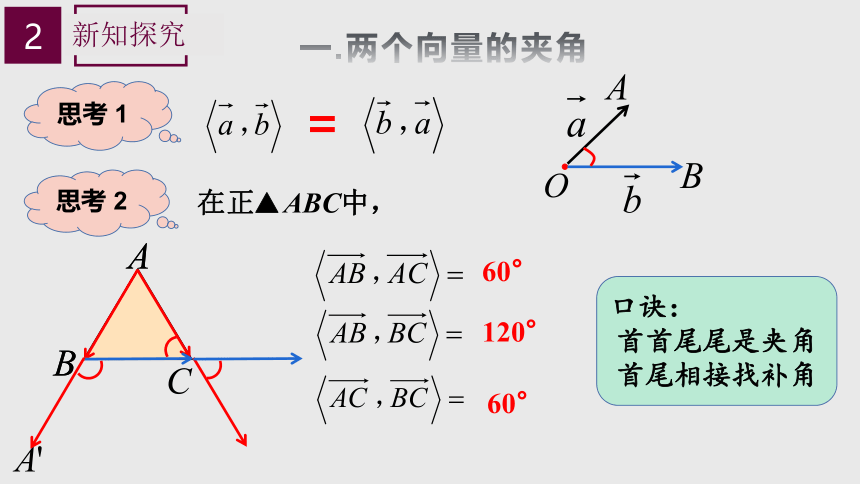
思考 1
=
思考 2
在正 ABC中,
60°
120°
60°
口诀:
首首尾尾是夹角
首尾相接找补角
一.两个向量的夹角
新知探究
2
练习1.判断
(1)在锐角▲ABC中,向量 与 的夹角等于向量 与 的夹角.
(2)对于非零向量a,b,=. ( )
练习2.在如图所示的正方体中,下列各对向量的夹角为45°的是( )
A
√
新知探究
2
零向量与任意向量的数量积为 .
0
实数
二.空间向量的数量积
新知探究
2
投影向量
新知探究
2
二.空间向量的数量积
新知探究
2
二.空间向量的数量积
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
新知探究
2
二.空间向量的数量积
2.如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
请类比平面向量的数量积运算,思考下面两个问题:
问题1.如果空间向量 是两个非零向量,它们的数量积有哪些性质呢?
问题2.空间向量数量积的运算律有哪些?
二.空间向量的数量积
问题1.如果空间向量 是两个非零向量,它们的数量积有哪些性质呢?
>0
<0
问题2.空间向量数量积的运算律有哪些?
数乘向量与向量
数量积的结合律
交换律
分配律
平面向量数量积的运算律
问题2.空间向量数量积的运算律有哪些?
数乘向量与向量
数量积的结合律
交换律
分配律
空间向量数量积的运算律
思考辨析?
非零向量 数量积运算
数量积运算 可约吗?
可除吗?
可结合吗?
不约
不除
不结合
误区
练习3.判断 是锐角的充要条件是
练习4.
①已知i,j,k是两两垂直的单位向量,a=2i-j+k,b=i+j-3k,则a·b=______
②已知|a|=13,|b|=19,|a+b|=24,则|a-b|=____.
③已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
-2
课堂练习
3
22
60。
空间向量数量积的应用
(1)求线段长度(距离):把所求线段看成一个向量的模,并用其它已知向量表示它,再用数量积运算求该向量的模;
(2)求夹角:
cos=
(3)证明垂直:
a⊥b a · b=0.
课堂练习
3
A
B
C
D
练习5.如图,在直三棱柱ABC A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,求 的值.
课堂练习
3
变式.本例中条件不变,N是AA1中点,求 的值.
课堂练习
3
课堂练习
3
l
m
n
g
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
练习6.如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.求证:PA⊥BD.
证:在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
③
课堂练习
3
课堂小结
4
1.1.2 空间向量的数量积运算
新知探究
2
新知引入
1
教学目标:
(1)通过类比的思想,理解和掌握空间向量数量积的定义、性质以及运算律;(2)掌握空间向量投影及投影向量,理解空间向量数量积的几何意义;
(3)基本掌握空间向量数量积运算解决空间距离、夹角问题.进一步体会空间向量解决立体几何问题的思想与方法.
教学重点:空间向量的数量积极概念以及空间向量投影
教学难点:空间向量的投影以及数量积的分配律;用空间向量表示所涉及的几何元素.
平面向量及其线性运算
空间向量及其线性运算
推 广
平面向量的数量积运算
空间向量的数量积运算
推 广
新知引入
1
思考 学习平面向量时,是如何研究它的数量积运算的?
夹角
数量积的定义
运算律
应用
新知引入
1
一.两个向量的夹角
定义:已知两个非零向量
在空间任取一点O,
则∠AOB叫做向量
的夹角,
记法:
作
范围:
新知探究
2
一.两个向量的夹角
新知探究
2
思考 1
=
思考 2
在正 ABC中,
60°
120°
60°
口诀:
首首尾尾是夹角
首尾相接找补角
一.两个向量的夹角
新知探究
2
练习1.判断
(1)在锐角▲ABC中,向量 与 的夹角等于向量 与 的夹角.
(2)对于非零向量a,b,
练习2.在如图所示的正方体中,下列各对向量的夹角为45°的是( )
A
√
新知探究
2
零向量与任意向量的数量积为 .
0
实数
二.空间向量的数量积
新知探究
2
投影向量
新知探究
2
二.空间向量的数量积
新知探究
2
二.空间向量的数量积
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
新知探究
2
二.空间向量的数量积
2.如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
请类比平面向量的数量积运算,思考下面两个问题:
问题1.如果空间向量 是两个非零向量,它们的数量积有哪些性质呢?
问题2.空间向量数量积的运算律有哪些?
二.空间向量的数量积
问题1.如果空间向量 是两个非零向量,它们的数量积有哪些性质呢?
>0
<0
问题2.空间向量数量积的运算律有哪些?
数乘向量与向量
数量积的结合律
交换律
分配律
平面向量数量积的运算律
问题2.空间向量数量积的运算律有哪些?
数乘向量与向量
数量积的结合律
交换律
分配律
空间向量数量积的运算律
思考辨析?
非零向量 数量积运算
数量积运算 可约吗?
可除吗?
可结合吗?
不约
不除
不结合
误区
练习3.判断 是锐角的充要条件是
练习4.
①已知i,j,k是两两垂直的单位向量,a=2i-j+k,b=i+j-3k,则a·b=______
②已知|a|=13,|b|=19,|a+b|=24,则|a-b|=____.
③已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
-2
课堂练习
3
22
60。
空间向量数量积的应用
(1)求线段长度(距离):把所求线段看成一个向量的模,并用其它已知向量表示它,再用数量积运算求该向量的模;
(2)求夹角:
cos
(3)证明垂直:
a⊥b a · b=0.
课堂练习
3
A
B
C
D
练习5.如图,在直三棱柱ABC A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,求 的值.
课堂练习
3
变式.本例中条件不变,N是AA1中点,求 的值.
课堂练习
3
课堂练习
3
l
m
n
g
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
练习6.如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.求证:PA⊥BD.
证:在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
③
课堂练习
3
课堂小结
4
