人教A版选择性必修一 2.2 直线的方程 课件(24张PPT)
文档属性
| 名称 | 人教A版选择性必修一 2.2 直线的方程 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:55:06 | ||
图片预览






文档简介
(共24张PPT)
2.2直线的方程
年 级:高 二
学 科:高中数学(人教版)
目录
一、知识体系
二、知识深度理解
三、求直线的方程
四、直线方程的综合应用
解析几何由17世纪法国数学家笛卡儿和费马创立.笛卡尔对现代数学的发展做出了重要的贡献,他于1637年发明了现代数学的基本工具——坐标系,将几何和代数相结合,创立了解析几何学。
数学从此进入变量数学时期,为微积分的创建奠定了基础.
解析几何学的创立者
法国数学家(1596-1650)
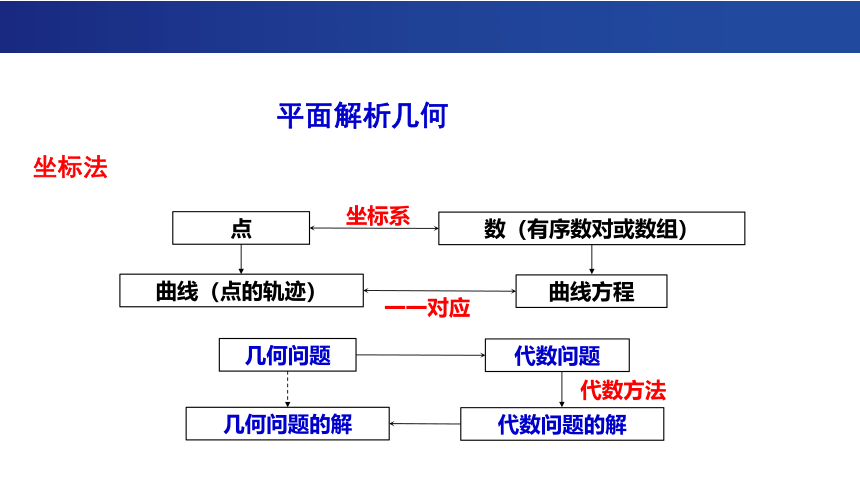
坐标法
点
数(有序数对或数组)
曲线(点的轨迹)
曲线方程
坐标系
一一对应
代数方法
几何问题
代数问题的解
代数问题
几何问题的解
平面解析几何
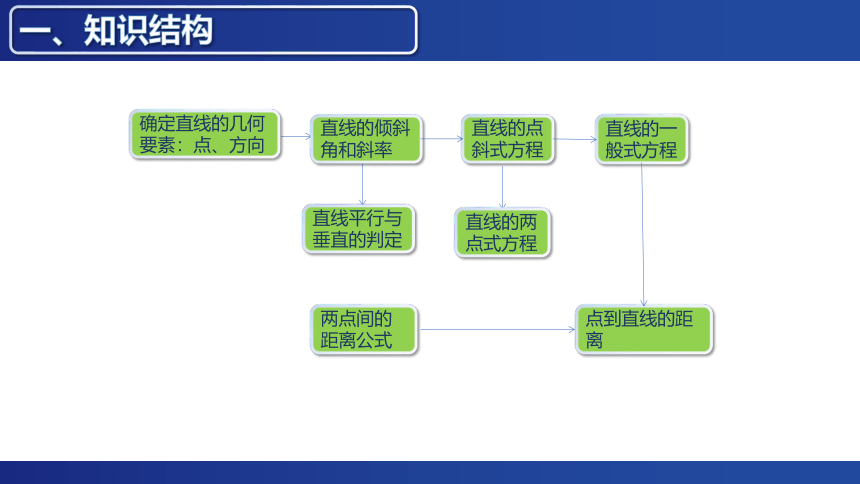
一、知识结构
确定直线的几何
要素:点、方向
直线的倾斜角和斜率
直线的点
斜式方程
直线的一般式方程
直线平行与垂直的判定
直线的两
点式方程
两点间的
距离公式
点到直线的距离
C
二、知识深度理解
直线的倾斜角与斜率
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角.
规定 : 当直线l与x轴平行或重合时,它的倾斜角为 .
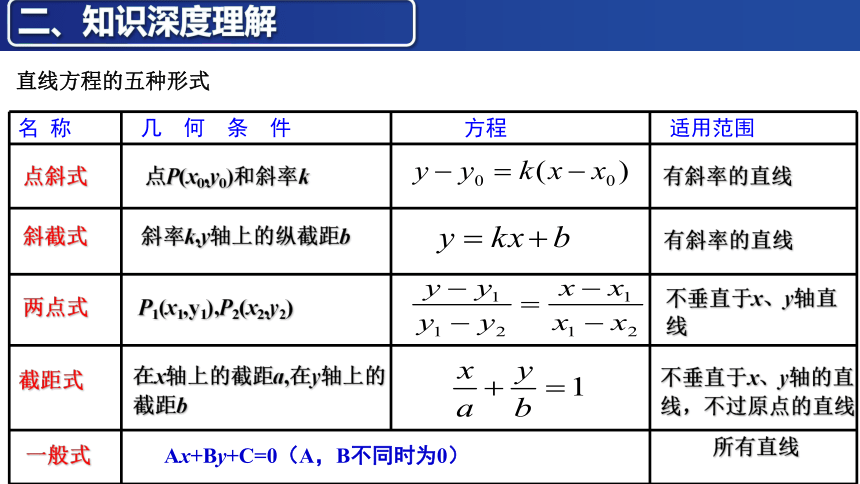
名 称 几 何 条 件 方程 适用范围
点P(x0,y0)和斜率k
点斜式
斜截式
两点式
截距式
斜率k,y轴上的纵截距b
在x轴上的截距a,在y轴上的截距b
P1(x1,y1),P2(x2,y2)
有斜率的直线
有斜率的直线
不垂直于x、y轴直线
不垂直于x、y轴的直线,不过原点的直线
Ax+By+C=0(A,B不同时为0)
所有直线
一般式
二、知识深度理解
直线方程的五种形式
C
二、知识深度理解
两直线的位置关系
直线方程
位置关系
重 合
平 行
垂 直
相 交
二、知识深度理解
C
二、知识深度理解
直线系方程
A1x+B1y+C1+λ( A2x+B2y+C2)=0是过直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程。
不包括A2x+B2y+C2=0这条直线
1)与直线l: 平行的直线系方程为:
(其中m≠C,m为待定系数)
2)与直线l: 垂直的直线系方程为:
(其中m为待定系数)
二、知识深度理解
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(1)求经过点(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍;
(3)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(1)求经过点(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程;
不要忘记过原点
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍;
(2)由已知设直线y=3x的倾斜角为α,则所求直线的倾斜角为2α.
因为tan α=3,
即3x+4y+15=0.
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(3)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.
(3)由题意可知,所求直线的斜率为±1.又过点(3,4),由点斜式得
y-4=±(x-3).
故所求直线的方程为x-y+1=0或x+y-7=0.
解题心得 1.求解直线方程的两种方法
2.谨防三种失误
(1)应用点斜式方程和斜截式方程时,要注意讨论斜率是否存在.
(2)应用截距式方程时,要注意讨论直线是否过原点,即截距是否为0.
(3)应用一般式Ax+By+C=0(A2+B2≠0)确定直线的斜率时,注意讨论B是否
为0.
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程
待定系 数法 ①设所求直线方程的某种形式;
②根据条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(1)若本例条件不变,求|OA|+|OB|的最小值及此时l的方程.
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(1)若本例条件不变,求|OA|+|OB|的最小值及此时l的方程.
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(2)若本例条件不变,求 的最大值及此时直线l的方程.
四、直线方程的综合应用
解题心得
求解与直线方程有关的最值问题.先设出直线方程,建立目标函数,再利用函数的单调性或均值不等式求解.
总结:
本节课你学到了什么?
2.2直线的方程
年 级:高 二
学 科:高中数学(人教版)
目录
一、知识体系
二、知识深度理解
三、求直线的方程
四、直线方程的综合应用
解析几何由17世纪法国数学家笛卡儿和费马创立.笛卡尔对现代数学的发展做出了重要的贡献,他于1637年发明了现代数学的基本工具——坐标系,将几何和代数相结合,创立了解析几何学。
数学从此进入变量数学时期,为微积分的创建奠定了基础.
解析几何学的创立者
法国数学家(1596-1650)
坐标法
点
数(有序数对或数组)
曲线(点的轨迹)
曲线方程
坐标系
一一对应
代数方法
几何问题
代数问题的解
代数问题
几何问题的解
平面解析几何
一、知识结构
确定直线的几何
要素:点、方向
直线的倾斜角和斜率
直线的点
斜式方程
直线的一般式方程
直线平行与垂直的判定
直线的两
点式方程
两点间的
距离公式
点到直线的距离
C
二、知识深度理解
直线的倾斜角与斜率
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角.
规定 : 当直线l与x轴平行或重合时,它的倾斜角为 .
名 称 几 何 条 件 方程 适用范围
点P(x0,y0)和斜率k
点斜式
斜截式
两点式
截距式
斜率k,y轴上的纵截距b
在x轴上的截距a,在y轴上的截距b
P1(x1,y1),P2(x2,y2)
有斜率的直线
有斜率的直线
不垂直于x、y轴直线
不垂直于x、y轴的直线,不过原点的直线
Ax+By+C=0(A,B不同时为0)
所有直线
一般式
二、知识深度理解
直线方程的五种形式
C
二、知识深度理解
两直线的位置关系
直线方程
位置关系
重 合
平 行
垂 直
相 交
二、知识深度理解
C
二、知识深度理解
直线系方程
A1x+B1y+C1+λ( A2x+B2y+C2)=0是过直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程。
不包括A2x+B2y+C2=0这条直线
1)与直线l: 平行的直线系方程为:
(其中m≠C,m为待定系数)
2)与直线l: 垂直的直线系方程为:
(其中m为待定系数)
二、知识深度理解
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(1)求经过点(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍;
(3)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(1)求经过点(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程;
不要忘记过原点
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍;
(2)由已知设直线y=3x的倾斜角为α,则所求直线的倾斜角为2α.
因为tan α=3,
即3x+4y+15=0.
C
三、求直线的方程
【例1】 求适合下列条件的直线方程:
(3)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.
(3)由题意可知,所求直线的斜率为±1.又过点(3,4),由点斜式得
y-4=±(x-3).
故所求直线的方程为x-y+1=0或x+y-7=0.
解题心得 1.求解直线方程的两种方法
2.谨防三种失误
(1)应用点斜式方程和斜截式方程时,要注意讨论斜率是否存在.
(2)应用截距式方程时,要注意讨论直线是否过原点,即截距是否为0.
(3)应用一般式Ax+By+C=0(A2+B2≠0)确定直线的斜率时,注意讨论B是否
为0.
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程
待定系 数法 ①设所求直线方程的某种形式;
②根据条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(1)若本例条件不变,求|OA|+|OB|的最小值及此时l的方程.
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(1)若本例条件不变,求|OA|+|OB|的最小值及此时l的方程.
【例2】 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△AOB的面积的最小值及此时直线l的方程.
四、直线方程的综合应用
变式发散
(2)若本例条件不变,求 的最大值及此时直线l的方程.
四、直线方程的综合应用
解题心得
求解与直线方程有关的最值问题.先设出直线方程,建立目标函数,再利用函数的单调性或均值不等式求解.
总结:
本节课你学到了什么?
