人教A版选择性必修一 3.1.2 椭圆的简单几何性质 课件(21张PPT)
文档属性
| 名称 | 人教A版选择性必修一 3.1.2 椭圆的简单几何性质 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:56:23 | ||
图片预览








文档简介
(共21张PPT)
3.1.2椭圆的简单几何性质2
学习目标:
1.了解椭圆在实际生活中的应用;
2.通过具体例子感受椭圆的另外一种定义方式;
3.认识直线与椭圆的位置关系,更好掌握运用方程研究曲线问题的基本思路和方法,培养学生的直观想象、数学运算、逻辑推理等素养.
重点:直线与椭圆位置关系的判断、弦长、中点弦的有关计算方法.
难点:方程研究曲线问题的基本思路和方法.
和椭圆有关的实际问题
1
例5.如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位于另一个焦点上.由椭圆一个焦点发出的光线,经过旋转椭圆面反射后集中到另一个焦点.已知,,.试建立适当的平面直角坐标系,求截口所在椭圆的方程(精确到).
l
求动点轨迹
2
例6.动点与定点的距离和到定直线的距离的比是常数,求动点的轨迹.
求动点轨迹
2
l
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
O
x
y
M
H
F
l
d
l′
F′
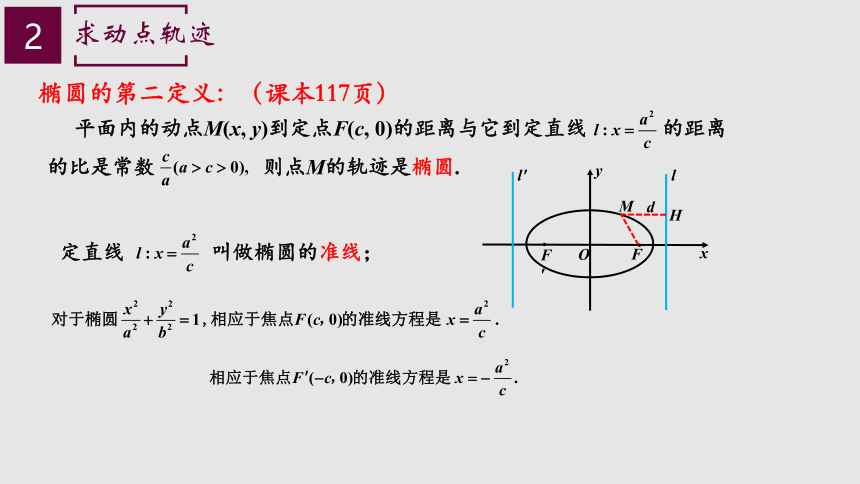
椭圆的第二定义:(课本117页)
求动点轨迹
2
定直线 叫做椭圆的准线;
O
x
y
M
H
F
l
d
l′
F′
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
椭圆的第二定义:(课本117页)
求动点轨迹
2
点与椭圆的位置关系
3
点P(x0,y0)与椭圆(a>b>0)的位置关系:
(1)点P在椭圆上 + 1;
(2)点P在椭圆内部 1;
(3)点P在椭圆外部 1.
直线与椭圆的位置关系
4
例7.如图,已知直线和椭圆.为何值时,直线与椭圆:(1)有两个公共点?(2)有且仅有一个公共点?(3)没有公共点?
直线与椭圆的位置关系
4
总结:判断直线与椭圆位置关系的方法:
弦长问题
5
追问:例7中直线和椭圆有两个公共点时,怎么求弦长?
l
O
x
y
F2
l
F1
A
B
解:设两个交点是A(x1,y1),B(x2,y2)
弦长问题
5
O
x
y
F2
l
F1
A
B
练:1.(课本P114, 2)经过椭圆 的左焦点F1作倾斜角为60°的直线l,直线l与椭圆相交于A,B两点,求AB的长.
弦长问题
5
O
x
y
F2
l
F1
A
B
弦长问题
5
练2.已知椭圆有两个顶点,过其焦点的直线与椭圆交于两点,若,求直线的方程.
由已知得,,所以.
所以椭圆方程为.
解:因为椭圆的焦点在轴上,设椭圆的标准方程为,
故设直线的方程为,联立椭圆方程,化简,
得.
弦长问题
5
练2.已知椭圆有两个顶点,过其焦点的直线与椭圆交于两点,若,求直线的方程.
.
设,则,.
由已知得,解得.
所以直线的方程为或.
中点弦问题
6
例8.已知椭圆的弦的中点P坐标为,求直线的方程.
中点弦问题
6
例8.已知椭圆的弦的中点P坐标为,求直线的方程.
∴,即.
中点弦问题
6
总结:中点弦问题,一般采用两种方法解决
(1)联立方程组,消元,利用根与系数的关系进行设而不求,从而简化运算.
(2)利用“点差法”即若椭圆方程为 ,直线与椭圆交于点A(x1,y1),B(x2,y2),且弦AB的中点为M(x,y),则 ① , ②
①-②:a2(-)+b2(-)=0,
∴==·.
这样就建立了中点坐标与直线的斜率之间的关系,从而使问题得以解决.
中点弦问题
6
练3.已知点是直线被焦点在轴上的椭圆所截得的线段的中点,则该椭圆的离心率为_______.
则 ①②得
即.
解:设椭圆方程为,直线与椭圆交于两点,且.
∵,中点为,∴即,
∴该椭圆的离心率为.
课堂小结
7
1.椭圆的第二定义;
2.点、直线与椭圆位置关系及判断方法;
3.弦长求法及弦长公式;
4.有关中点弦问题方法.
感谢倾听!
3.1.2椭圆的简单几何性质2
学习目标:
1.了解椭圆在实际生活中的应用;
2.通过具体例子感受椭圆的另外一种定义方式;
3.认识直线与椭圆的位置关系,更好掌握运用方程研究曲线问题的基本思路和方法,培养学生的直观想象、数学运算、逻辑推理等素养.
重点:直线与椭圆位置关系的判断、弦长、中点弦的有关计算方法.
难点:方程研究曲线问题的基本思路和方法.
和椭圆有关的实际问题
1
例5.如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位于另一个焦点上.由椭圆一个焦点发出的光线,经过旋转椭圆面反射后集中到另一个焦点.已知,,.试建立适当的平面直角坐标系,求截口所在椭圆的方程(精确到).
l
求动点轨迹
2
例6.动点与定点的距离和到定直线的距离的比是常数,求动点的轨迹.
求动点轨迹
2
l
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
O
x
y
M
H
F
l
d
l′
F′
椭圆的第二定义:(课本117页)
求动点轨迹
2
定直线 叫做椭圆的准线;
O
x
y
M
H
F
l
d
l′
F′
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
椭圆的第二定义:(课本117页)
求动点轨迹
2
点与椭圆的位置关系
3
点P(x0,y0)与椭圆(a>b>0)的位置关系:
(1)点P在椭圆上 + 1;
(2)点P在椭圆内部 1;
(3)点P在椭圆外部 1.
直线与椭圆的位置关系
4
例7.如图,已知直线和椭圆.为何值时,直线与椭圆:(1)有两个公共点?(2)有且仅有一个公共点?(3)没有公共点?
直线与椭圆的位置关系
4
总结:判断直线与椭圆位置关系的方法:
弦长问题
5
追问:例7中直线和椭圆有两个公共点时,怎么求弦长?
l
O
x
y
F2
l
F1
A
B
解:设两个交点是A(x1,y1),B(x2,y2)
弦长问题
5
O
x
y
F2
l
F1
A
B
练:1.(课本P114, 2)经过椭圆 的左焦点F1作倾斜角为60°的直线l,直线l与椭圆相交于A,B两点,求AB的长.
弦长问题
5
O
x
y
F2
l
F1
A
B
弦长问题
5
练2.已知椭圆有两个顶点,过其焦点的直线与椭圆交于两点,若,求直线的方程.
由已知得,,所以.
所以椭圆方程为.
解:因为椭圆的焦点在轴上,设椭圆的标准方程为,
故设直线的方程为,联立椭圆方程,化简,
得.
弦长问题
5
练2.已知椭圆有两个顶点,过其焦点的直线与椭圆交于两点,若,求直线的方程.
.
设,则,.
由已知得,解得.
所以直线的方程为或.
中点弦问题
6
例8.已知椭圆的弦的中点P坐标为,求直线的方程.
中点弦问题
6
例8.已知椭圆的弦的中点P坐标为,求直线的方程.
∴,即.
中点弦问题
6
总结:中点弦问题,一般采用两种方法解决
(1)联立方程组,消元,利用根与系数的关系进行设而不求,从而简化运算.
(2)利用“点差法”即若椭圆方程为 ,直线与椭圆交于点A(x1,y1),B(x2,y2),且弦AB的中点为M(x,y),则 ① , ②
①-②:a2(-)+b2(-)=0,
∴==·.
这样就建立了中点坐标与直线的斜率之间的关系,从而使问题得以解决.
中点弦问题
6
练3.已知点是直线被焦点在轴上的椭圆所截得的线段的中点,则该椭圆的离心率为_______.
则 ①②得
即.
解:设椭圆方程为,直线与椭圆交于两点,且.
∵,中点为,∴即,
∴该椭圆的离心率为.
课堂小结
7
1.椭圆的第二定义;
2.点、直线与椭圆位置关系及判断方法;
3.弦长求法及弦长公式;
4.有关中点弦问题方法.
感谢倾听!
