总复习 图形与几何 课件 六年级上册数学 人教版(共25张PPT)
文档属性
| 名称 | 总复习 图形与几何 课件 六年级上册数学 人教版(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 723.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 08:07:57 | ||
图片预览



文档简介
(共25张PPT)
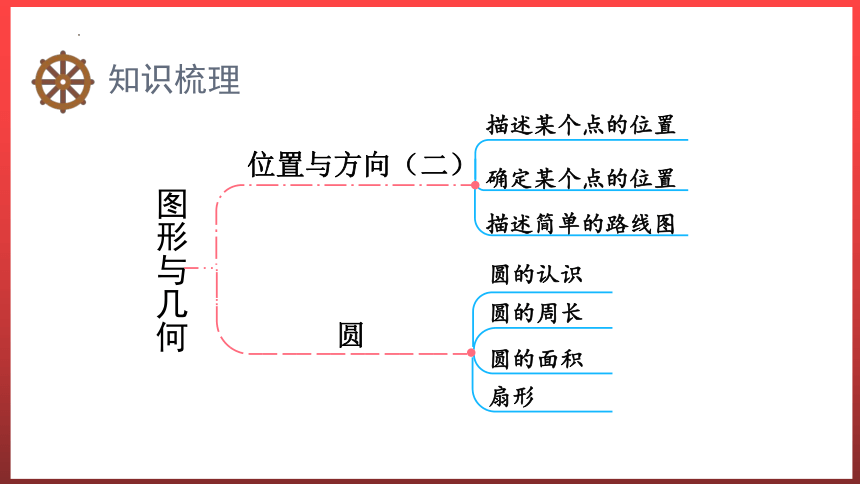
图形与几何
图形与几何
位置与方向(二)
描述某个点的位置
确定某个点的位置
描述简单的路线图
圆
圆的认识
圆的面积
扇形
圆的周长
位置与方向(二)
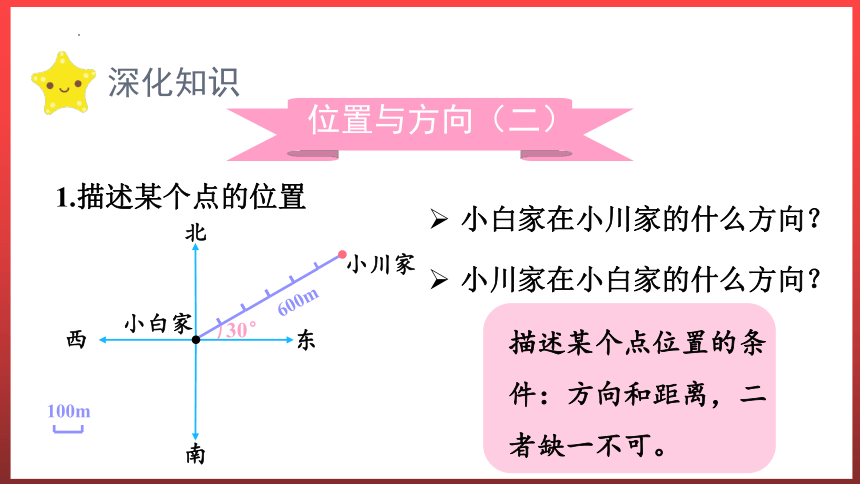
1.描述某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
小白家在小川家的什么方向?
小川家在小白家的什么方向?
描述某个点位置的条件:方向和距离,二者缺一不可。
学校
45°
500m
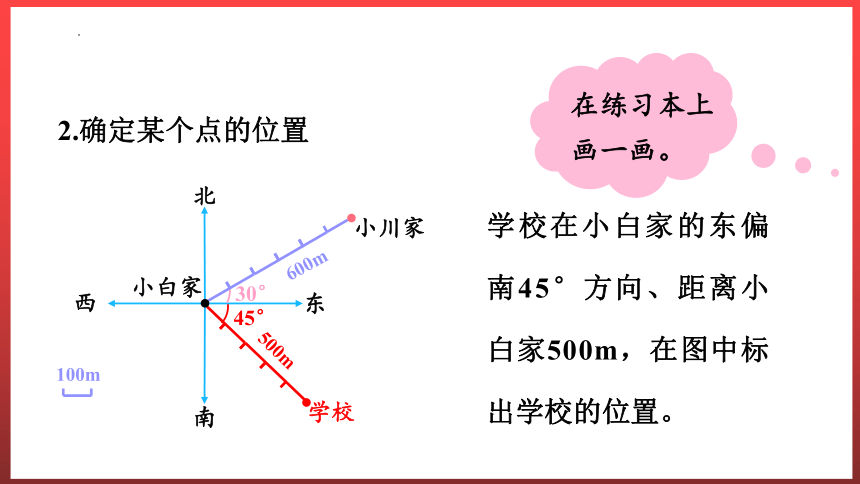
2.确定某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
学校在小白家的东偏南45°方向、距离小白家500m,在图中标出学校的位置。
在练习本上画一画。
学校
45°
500m
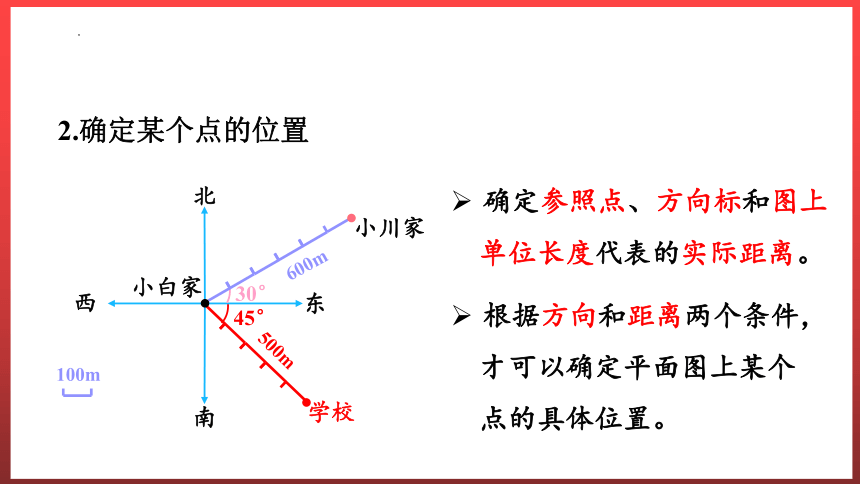
2.确定某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
确定参照点、方向标和图上
单位长度代表的实际距离。
根据方向和距离两个条件,
才可以确定平面图上某个
点的具体位置。
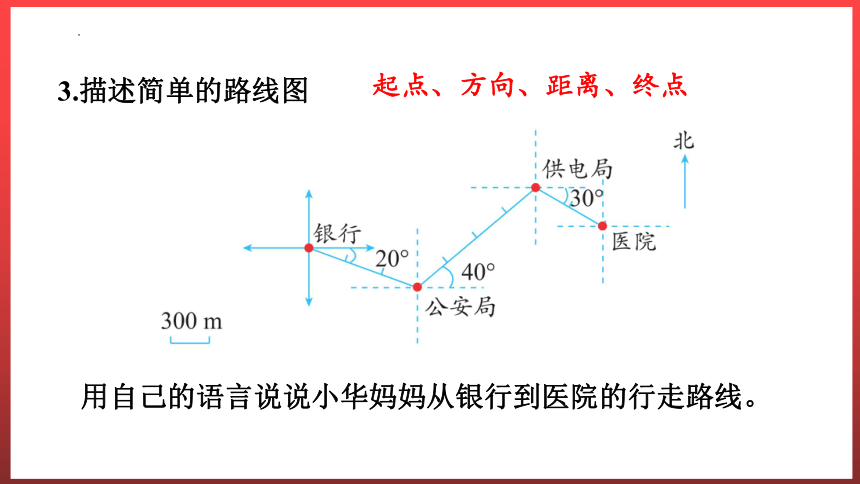
3.描述简单的路线图
用自己的语言说说小华妈妈从银行到医院的行走路线。
起点、方向、距离、终点
1.圆的认识
圆
O
r
d
一个圆心(O)
无数条半径(r)和直径(d)
圆的位置
决定
圆的大小
决定
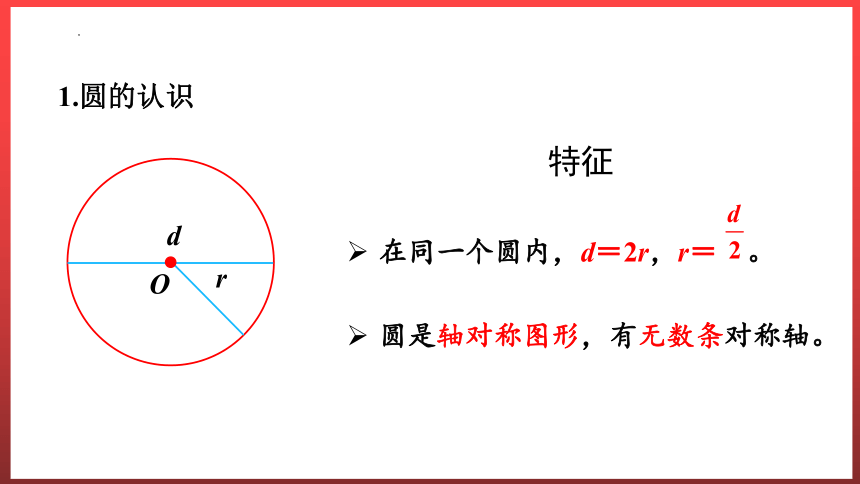
1.圆的认识
O
r
d
特征
在同一个圆内,d=2r,r= 。
圆是轴对称图形,有无数条对称轴。
2.圆的周长
r=4cm
探究活动
1.什么是圆的周长?
2.圆的周长的测量方法有哪些?
运用了什么转化方法?
3.说一说圆周率的意义。
4.写一写圆的周长的计算公式。
5.算一算左边圆的周长。
2.圆的周长
r=4cm
圆的周长的测量方法:
直接测量法
滚动法
绕绳法
化曲为直
2.圆的周长
r=4cm
= 圆周率π
≈ 3.14
无限不循环小数
π ≈ 3.1415926535……
2.圆的周长
r=4cm
计算公式:
C=πd
C=2πr
2×3.14×4
= 6.28×4
= 25.12(cm)
3.圆的面积
r=4cm
探究活动
1.什么是圆的面积?
2.圆的面积计算公式的推导过程是怎样的?运用了什么转化方法?
3.写一写圆的面积的计算公式。
4.算一算左边圆的面积。
三十二等分
3.圆的面积
化曲为直
极限思想
3.圆的面积
r=4cm
计算公式:
S=πr2
3.14×42
= 3.14×16
= 50.24(cm2)
4.圆环的面积
r=3cm
R=5cm
探究活动
1.什么是圆环?它是怎样得到的?
2.写一写圆环的面积的计算公式。
3.算一算左边圆环的面积。
4.圆环的面积
r=3cm
R=5cm
计算公式:
S环=πR2- πr2
3.14×(52-32 )
=3.14×16
=50.24(cm2)
S环=π(R2- r2)
5.扇形
B
A
弧
一条弧和经过这条弧两端的半径所围成的图形叫做扇形。
扇形是轴对称图形,它只有一条对称轴。
在同一个圆中扇形的大小与圆心角的大小有关。
O
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)这个公园的围墙有多长?
2×3.14×1= 6.28(km)
答:这个公园的围墙有6.28km。
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(2)北门在南门的什么方向?
距离南门有多远?
1+1= 2(km)
答:北门在南门的正北方,距
离南门2km。
(3)如果公园里有一个半径为0.2km的圆形小湖,这个
公园的陆地面积是多少平方千米?
3.14×12-3.14×0.22
=3.14×1-3.14×0.04
=3.14-0.1256
=3.0144(平方千米)
答:这个公园的陆地面积是
3.0144平方千米。
1km
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(4)请你再提出一些数学问题
并试着解决。
同桌合作完成。
用三张同样大小的正方形白铁皮(边长是1.8m),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
d=1.8m
第一种圆片:3.14×1.8=5.652(m)
d=(1.8÷2)m
第二种圆片:3.14×(1.8÷2)=2.826(m)
d=(1.8÷3)m
第三种圆片:3.14×(1.8÷3)=1.884(m)
(2)剪完圆后,哪张白铁皮剩下的废料多些?
第一张白铁皮:1.82-3.14×(1.8÷2)2=0.6966(m2)
第二张白铁皮:1.82-3.14×(1.8÷2÷2)2 ×4=0.6966(m2)
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
第三张白铁皮:1.82-3.14×(1.8÷3÷2)2 ×9=0.6966(m2)
答:剪完圆后,剩下的废料同样多。
(3)根据以上的计算,你发现了什么?
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
剪掉16个圆:
按这样的方式剪圆,无论怎么减,剩下的废料总是不变的。
1.82-3.14×(1.8÷4÷2)2 ×16=0.6966(m2)
图形与几何
图形与几何
位置与方向(二)
描述某个点的位置
确定某个点的位置
描述简单的路线图
圆
圆的认识
圆的面积
扇形
圆的周长
位置与方向(二)
1.描述某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
小白家在小川家的什么方向?
小川家在小白家的什么方向?
描述某个点位置的条件:方向和距离,二者缺一不可。
学校
45°
500m
2.确定某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
学校在小白家的东偏南45°方向、距离小白家500m,在图中标出学校的位置。
在练习本上画一画。
学校
45°
500m
2.确定某个点的位置
北
南
西
东
小川家
30°
小白家
100m
600m
确定参照点、方向标和图上
单位长度代表的实际距离。
根据方向和距离两个条件,
才可以确定平面图上某个
点的具体位置。
3.描述简单的路线图
用自己的语言说说小华妈妈从银行到医院的行走路线。
起点、方向、距离、终点
1.圆的认识
圆
O
r
d
一个圆心(O)
无数条半径(r)和直径(d)
圆的位置
决定
圆的大小
决定
1.圆的认识
O
r
d
特征
在同一个圆内,d=2r,r= 。
圆是轴对称图形,有无数条对称轴。
2.圆的周长
r=4cm
探究活动
1.什么是圆的周长?
2.圆的周长的测量方法有哪些?
运用了什么转化方法?
3.说一说圆周率的意义。
4.写一写圆的周长的计算公式。
5.算一算左边圆的周长。
2.圆的周长
r=4cm
圆的周长的测量方法:
直接测量法
滚动法
绕绳法
化曲为直
2.圆的周长
r=4cm
= 圆周率π
≈ 3.14
无限不循环小数
π ≈ 3.1415926535……
2.圆的周长
r=4cm
计算公式:
C=πd
C=2πr
2×3.14×4
= 6.28×4
= 25.12(cm)
3.圆的面积
r=4cm
探究活动
1.什么是圆的面积?
2.圆的面积计算公式的推导过程是怎样的?运用了什么转化方法?
3.写一写圆的面积的计算公式。
4.算一算左边圆的面积。
三十二等分
3.圆的面积
化曲为直
极限思想
3.圆的面积
r=4cm
计算公式:
S=πr2
3.14×42
= 3.14×16
= 50.24(cm2)
4.圆环的面积
r=3cm
R=5cm
探究活动
1.什么是圆环?它是怎样得到的?
2.写一写圆环的面积的计算公式。
3.算一算左边圆环的面积。
4.圆环的面积
r=3cm
R=5cm
计算公式:
S环=πR2- πr2
3.14×(52-32 )
=3.14×16
=50.24(cm2)
S环=π(R2- r2)
5.扇形
B
A
弧
一条弧和经过这条弧两端的半径所围成的图形叫做扇形。
扇形是轴对称图形,它只有一条对称轴。
在同一个圆中扇形的大小与圆心角的大小有关。
O
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)这个公园的围墙有多长?
2×3.14×1= 6.28(km)
答:这个公园的围墙有6.28km。
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(2)北门在南门的什么方向?
距离南门有多远?
1+1= 2(km)
答:北门在南门的正北方,距
离南门2km。
(3)如果公园里有一个半径为0.2km的圆形小湖,这个
公园的陆地面积是多少平方千米?
3.14×12-3.14×0.22
=3.14×1-3.14×0.04
=3.14-0.1256
=3.0144(平方千米)
答:这个公园的陆地面积是
3.0144平方千米。
1km
1.一个公园是圆形布局,半径长 1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(4)请你再提出一些数学问题
并试着解决。
同桌合作完成。
用三张同样大小的正方形白铁皮(边长是1.8m),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
d=1.8m
第一种圆片:3.14×1.8=5.652(m)
d=(1.8÷2)m
第二种圆片:3.14×(1.8÷2)=2.826(m)
d=(1.8÷3)m
第三种圆片:3.14×(1.8÷3)=1.884(m)
(2)剪完圆后,哪张白铁皮剩下的废料多些?
第一张白铁皮:1.82-3.14×(1.8÷2)2=0.6966(m2)
第二张白铁皮:1.82-3.14×(1.8÷2÷2)2 ×4=0.6966(m2)
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
第三张白铁皮:1.82-3.14×(1.8÷3÷2)2 ×9=0.6966(m2)
答:剪完圆后,剩下的废料同样多。
(3)根据以上的计算,你发现了什么?
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
剪掉16个圆:
按这样的方式剪圆,无论怎么减,剩下的废料总是不变的。
1.82-3.14×(1.8÷4÷2)2 ×16=0.6966(m2)
