人教版(2019)数学选择性必修三 6.2排列与组合课件(共43张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三 6.2排列与组合课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:27:14 | ||
图片预览








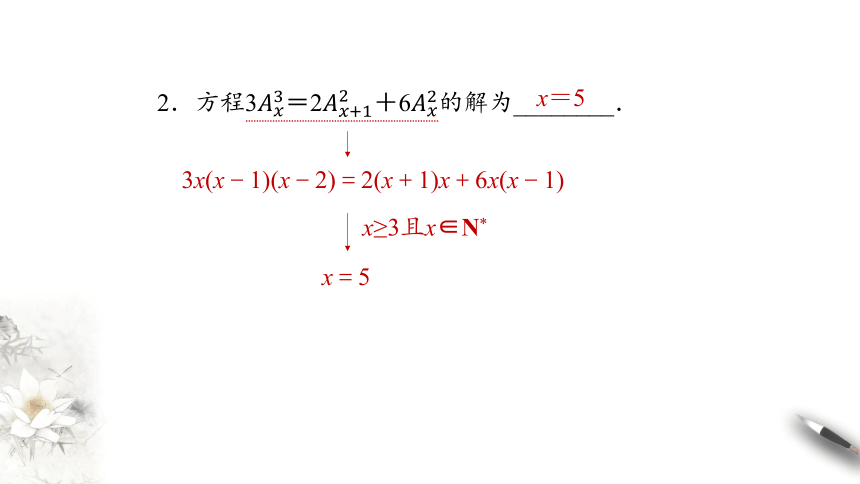



文档简介
(共43张PPT)
高二选择性必修三
排列与组合
新课程标准 考向预测 1.通过实例,理解排列、组合的概念. 2.能利用计数原理推导排列数公式、组合数公式. 命题角度 1.排列问题
2.组合问题
3.排列组合综合问题
核心素养 数学运算、逻辑推理
基础梳理
基础点一 排列与排列数
从n个不同元素中取出m(m≤n)个元素,按照__________排成一列,叫做从n个不同元素中取出m(m≤n)个元素的一个排列.
1.排列的定义
一定顺序
从n个不同元素中取出m(m≤n)个元素的所有__________的个数,叫做从n个不同元素中取出m(m≤n)个元素的排列数.用符号“”表示.
2.排列数的定义
不同排列
=__________________________=
(n,m∈N*,且m≤n).
3.排列数计算公式
n(n-1)(n-2)…(n-m+1)
n个不同元素全部取出的一个排列,叫做n个元素的一个全排列,记为: =n(n-1)(n-2)·…·2·1=______.
规定:0!=_____.
4.全排列
n!
1
1.排列是一个具体的排法,不是数是一件事,而排列数是所有排列的个数,是一个正整数.
易错提醒
2.计算时易错算为n(n-1)(n-2)…(n-m).
基础小测
1.(2020届四川成都经开区实验中学高三开学考试)某学校高三年级有2个文科班,3个理科班,现每个班指定1人对各班的卫生进行检查,若每班只安排一人检查,且文科班学生不检查文科班,理科班学生不检查自己所在的班,则不同安排方法的种数是( )
A.24 B.32 C.48 D.84
A
2.方程3=2+6的解为________.
x=5
3x(x-1)(x-2)=2(x+1)x+6x(x-1)
x≥3且x∈N*
x=5
基础点二 组合与组合数
从n个不同元素中取出m(m≤n)个元素__________,叫做从n个不同元素中取出m(m≤n)个元素的一个组合.
1.组合的定义
合成一组
从n个不同元素中取出m(m≤n)个元素的所有__________的个数,叫做从n个不同元素中取出m(m≤n)个元素的一个组合数,用符号“”表示.
2.组合数定义
不同组合
=__________________________=
(n,m∈N*,且m≤n).
3.组合数计算公式
n(n-1)(n-2)…(n-m+1)
m!
因为0!=1,所以=1.
(1)==________;
(2)________= ;
(3)=__________+.
4.组合数的性质
1
排列与组合最根本的区别在于“有序”和“无序”.取出元素后交换顺序,与顺序有关是排列,与顺序无关是组合.
特别提醒
基础小测
1.(2020届东北育才学校高考模拟)某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有( )
A.8种 B.12种 C.16种 D.20种
C
2.安排A,B,C,D,E,F,共6名义工照顾甲、乙、丙三位老人,每两位义工照顾一位老人,考虑到义工与老人住址距离问题,义工A不安排照顾老人甲,义工B不安排照顾老人乙,则安排方法共有( )
A.30种 B.40种
C.42种 D.48种
C
考点突破
考点一 排列问题(高考热度:★★)
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
从7人中选5人排列,有=7×6×5×4×3=2520(种).
(2)排成前后两排,前排3人,后排4人;
分两步完成,先选3人站前排,有种方法,余下4人站后排,有种方法,共有=5040(种).
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(3)全体排成一排,甲不站排头也不站排尾;
法一:(特殊元素优先法)
先排甲,有5种方法,其余6人有种排列方法,共有5×=3600(种).
首尾位置可安排另6人中的两人,有种排法,其他有种排法,共有=3600(种).
法二:(特殊位置优先法)
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(4)全体排成一排,女生必须站在一起;
将女生看作一个整体与3名男生一起全排列,有种方法,
再将女生全排列,有种方法,
共有· =576(种).
捆绑法
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(5)全体排成一排,男生互不相邻.
先排女生,有种方法,
再在女生之间及首尾5个空位中任选3个空位安排男生,有种方法,
共有· =1440(种).
插空法
求解排列应用问题的6种主要方法
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中
定序问题除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反、等价转化的方法
方法总结
考点微练
1.高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是( )
A.1800 B.3600
C.4320 D.5040
B
2.用数字0,1,2,3,4组成没有重复数字且大于3000的四位数,这样的四位数有( )
A.250个 B.249个
C.48个 D.24个
C
考点二 组合问题(高考热度:★★)
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
从余下的34种商品中,选取2种有=561(种)取法,
所以某一种假货必须在内的不同取法有561种.
(2)其中某一种假货不能在内,不同取法有多少种?
从34种可选商品中,选取3种,有种或者-==5984(种)取法.
所以某一种假货不能在内的不同取法有5984种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(3)恰有2种假货在内,不同取法有多少种?
从20种真货中选取1种,从15种假货中选取2种有=2100(种)取法.
所以恰有2种假货在内的不同的取法有2100种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(4)至少有2种假货在内,不同取法有多少种?
选取2种假货有种,选取3种假货有种,
共有选取方式+ =2100+455=2555(种).
所以至少有2种假货在内的不同的取法有2555种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(5)至多有2种假货在内,不同取法有多少种?
选取3种商品的总数为,因此共有选取方式
- =6545-455=6090(种).
所以至多有2种假货在内的不同的取法有6 090种.
法一:(间接法)
共有选取方式++ =6090(种).
所以至多有2种假货在内的不同的取法有6090种.
法二:(直接法)
组合问题的2类题型及求解方法
2. “至少”或“至多”含有几个元素的组合题型
解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
1. “含有”或“不含有”某些元素的组合题型
“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
方法总结
1.从{1,2,3,…,10}中选取三个不同的数,使得其中至少有两个相邻,则不同的选法种数是( )
A.72 B.70
C.66 D.64
考点微练
D
2.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种.(用数字作答)
16
考点三 排列、组合的综合问题(高考热度:★★★)
[例3] 把四个不同的小球放入三个分别标有1号、2号、3号的盒子中,不允许有空盒子的放法有( )
A.种 B. 种
C. 种 D.18种
BC
考向1 简单的排列、组合的综合问题
(1)根据附加条件将要完成事件先分类.
(2)对每一类型取出符合要求的元素组合,再对取出的元素排列.
(3)由分类加法计数原理计算总数.
解决简单的排列、组合综合问题的思路
解题通法
考向微练
1.习近平总书记在湖南省湘西土家族苗族自治州十八洞村考察时首次提出“精准扶贫”概念,精准扶贫成为我国脱贫攻坚的基本方略.
为配合国家精准扶贫战略,某省示范性高中安排6名高级教师(不同姓)到基础教育薄弱的甲、乙、丙三所中学进行扶贫支教,每所学校至少1人,因工作需要,其中李老师不去甲校,则分配方案种数为________.
360
考向2 分组、分配问题
[例4] 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种
C.24种 D.36种
D
[例5] 将5本不同的书分给甲、乙、丙三人,每人至少一本至多两本,则不同的分法种数是( )
A.60 B.90
C.120 D.180
B
考向2 分组、分配问题
(1)对不同元素的分配问题
①对于整体均分,解题时要注意分组后,不管它们的顺序如何,都是一种情况,所以分组后一定要除以A(n为均分的组数)避免重复计数.
②对于部分均分,解题时注意重复的次数是均匀分组的阶乘数,即若有m组元素个数相等,则分组时应除以m!,分组过程中有几个这样的均匀分组,就要除以几个这样的全排列数.
③对于不等分组,只需先分组,后排列,注意分组时任何组中元素的个数都不相等,所以不需要除以全排列数.
(2)对于相同元素的“分配”问题,常采用的方法是“隔板法”.
分组、分配问题的求解策略
归纳总结
考向微练
1.(2020届云南玉溪第一中学高考模拟)教育部选派3名中文教师到外国任教中文,有4个国家可供选择,每名教师随机选择一个国家,则恰有2名教师选择同一个国家的概率为( )
A . B. C. D.
C
2.(2020届重庆巴蜀中学高三月考)6个高矮互不相同的人站成两排,后排每个人都高于站在他前面的同学的概率为( )
A. B. C. D.
C
3.现有一圆桌,周边有标号为1,2,3,4的四个座位,甲、乙、丙、丁四位同学坐在一起探讨一个数学课题,每人只能坐一个座位,甲先选座位,且甲、乙不能相邻,则所有选座方法有________种(用数字作答).
8
通过本节课,你学会了什么?
高二选择性必修三
排列与组合
新课程标准 考向预测 1.通过实例,理解排列、组合的概念. 2.能利用计数原理推导排列数公式、组合数公式. 命题角度 1.排列问题
2.组合问题
3.排列组合综合问题
核心素养 数学运算、逻辑推理
基础梳理
基础点一 排列与排列数
从n个不同元素中取出m(m≤n)个元素,按照__________排成一列,叫做从n个不同元素中取出m(m≤n)个元素的一个排列.
1.排列的定义
一定顺序
从n个不同元素中取出m(m≤n)个元素的所有__________的个数,叫做从n个不同元素中取出m(m≤n)个元素的排列数.用符号“”表示.
2.排列数的定义
不同排列
=__________________________=
(n,m∈N*,且m≤n).
3.排列数计算公式
n(n-1)(n-2)…(n-m+1)
n个不同元素全部取出的一个排列,叫做n个元素的一个全排列,记为: =n(n-1)(n-2)·…·2·1=______.
规定:0!=_____.
4.全排列
n!
1
1.排列是一个具体的排法,不是数是一件事,而排列数是所有排列的个数,是一个正整数.
易错提醒
2.计算时易错算为n(n-1)(n-2)…(n-m).
基础小测
1.(2020届四川成都经开区实验中学高三开学考试)某学校高三年级有2个文科班,3个理科班,现每个班指定1人对各班的卫生进行检查,若每班只安排一人检查,且文科班学生不检查文科班,理科班学生不检查自己所在的班,则不同安排方法的种数是( )
A.24 B.32 C.48 D.84
A
2.方程3=2+6的解为________.
x=5
3x(x-1)(x-2)=2(x+1)x+6x(x-1)
x≥3且x∈N*
x=5
基础点二 组合与组合数
从n个不同元素中取出m(m≤n)个元素__________,叫做从n个不同元素中取出m(m≤n)个元素的一个组合.
1.组合的定义
合成一组
从n个不同元素中取出m(m≤n)个元素的所有__________的个数,叫做从n个不同元素中取出m(m≤n)个元素的一个组合数,用符号“”表示.
2.组合数定义
不同组合
=__________________________=
(n,m∈N*,且m≤n).
3.组合数计算公式
n(n-1)(n-2)…(n-m+1)
m!
因为0!=1,所以=1.
(1)==________;
(2)________= ;
(3)=__________+.
4.组合数的性质
1
排列与组合最根本的区别在于“有序”和“无序”.取出元素后交换顺序,与顺序有关是排列,与顺序无关是组合.
特别提醒
基础小测
1.(2020届东北育才学校高考模拟)某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有( )
A.8种 B.12种 C.16种 D.20种
C
2.安排A,B,C,D,E,F,共6名义工照顾甲、乙、丙三位老人,每两位义工照顾一位老人,考虑到义工与老人住址距离问题,义工A不安排照顾老人甲,义工B不安排照顾老人乙,则安排方法共有( )
A.30种 B.40种
C.42种 D.48种
C
考点突破
考点一 排列问题(高考热度:★★)
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
从7人中选5人排列,有=7×6×5×4×3=2520(种).
(2)排成前后两排,前排3人,后排4人;
分两步完成,先选3人站前排,有种方法,余下4人站后排,有种方法,共有=5040(种).
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(3)全体排成一排,甲不站排头也不站排尾;
法一:(特殊元素优先法)
先排甲,有5种方法,其余6人有种排列方法,共有5×=3600(种).
首尾位置可安排另6人中的两人,有种排法,其他有种排法,共有=3600(种).
法二:(特殊位置优先法)
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(4)全体排成一排,女生必须站在一起;
将女生看作一个整体与3名男生一起全排列,有种方法,
再将女生全排列,有种方法,
共有· =576(种).
捆绑法
[例1] 有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(5)全体排成一排,男生互不相邻.
先排女生,有种方法,
再在女生之间及首尾5个空位中任选3个空位安排男生,有种方法,
共有· =1440(种).
插空法
求解排列应用问题的6种主要方法
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中
定序问题除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反、等价转化的方法
方法总结
考点微练
1.高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是( )
A.1800 B.3600
C.4320 D.5040
B
2.用数字0,1,2,3,4组成没有重复数字且大于3000的四位数,这样的四位数有( )
A.250个 B.249个
C.48个 D.24个
C
考点二 组合问题(高考热度:★★)
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
从余下的34种商品中,选取2种有=561(种)取法,
所以某一种假货必须在内的不同取法有561种.
(2)其中某一种假货不能在内,不同取法有多少种?
从34种可选商品中,选取3种,有种或者-==5984(种)取法.
所以某一种假货不能在内的不同取法有5984种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(3)恰有2种假货在内,不同取法有多少种?
从20种真货中选取1种,从15种假货中选取2种有=2100(种)取法.
所以恰有2种假货在内的不同的取法有2100种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(4)至少有2种假货在内,不同取法有多少种?
选取2种假货有种,选取3种假货有种,
共有选取方式+ =2100+455=2555(种).
所以至少有2种假货在内的不同的取法有2555种.
[例2] 某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(5)至多有2种假货在内,不同取法有多少种?
选取3种商品的总数为,因此共有选取方式
- =6545-455=6090(种).
所以至多有2种假货在内的不同的取法有6 090种.
法一:(间接法)
共有选取方式++ =6090(种).
所以至多有2种假货在内的不同的取法有6090种.
法二:(直接法)
组合问题的2类题型及求解方法
2. “至少”或“至多”含有几个元素的组合题型
解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
1. “含有”或“不含有”某些元素的组合题型
“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
方法总结
1.从{1,2,3,…,10}中选取三个不同的数,使得其中至少有两个相邻,则不同的选法种数是( )
A.72 B.70
C.66 D.64
考点微练
D
2.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种.(用数字作答)
16
考点三 排列、组合的综合问题(高考热度:★★★)
[例3] 把四个不同的小球放入三个分别标有1号、2号、3号的盒子中,不允许有空盒子的放法有( )
A.种 B. 种
C. 种 D.18种
BC
考向1 简单的排列、组合的综合问题
(1)根据附加条件将要完成事件先分类.
(2)对每一类型取出符合要求的元素组合,再对取出的元素排列.
(3)由分类加法计数原理计算总数.
解决简单的排列、组合综合问题的思路
解题通法
考向微练
1.习近平总书记在湖南省湘西土家族苗族自治州十八洞村考察时首次提出“精准扶贫”概念,精准扶贫成为我国脱贫攻坚的基本方略.
为配合国家精准扶贫战略,某省示范性高中安排6名高级教师(不同姓)到基础教育薄弱的甲、乙、丙三所中学进行扶贫支教,每所学校至少1人,因工作需要,其中李老师不去甲校,则分配方案种数为________.
360
考向2 分组、分配问题
[例4] 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种
C.24种 D.36种
D
[例5] 将5本不同的书分给甲、乙、丙三人,每人至少一本至多两本,则不同的分法种数是( )
A.60 B.90
C.120 D.180
B
考向2 分组、分配问题
(1)对不同元素的分配问题
①对于整体均分,解题时要注意分组后,不管它们的顺序如何,都是一种情况,所以分组后一定要除以A(n为均分的组数)避免重复计数.
②对于部分均分,解题时注意重复的次数是均匀分组的阶乘数,即若有m组元素个数相等,则分组时应除以m!,分组过程中有几个这样的均匀分组,就要除以几个这样的全排列数.
③对于不等分组,只需先分组,后排列,注意分组时任何组中元素的个数都不相等,所以不需要除以全排列数.
(2)对于相同元素的“分配”问题,常采用的方法是“隔板法”.
分组、分配问题的求解策略
归纳总结
考向微练
1.(2020届云南玉溪第一中学高考模拟)教育部选派3名中文教师到外国任教中文,有4个国家可供选择,每名教师随机选择一个国家,则恰有2名教师选择同一个国家的概率为( )
A . B. C. D.
C
2.(2020届重庆巴蜀中学高三月考)6个高矮互不相同的人站成两排,后排每个人都高于站在他前面的同学的概率为( )
A. B. C. D.
C
3.现有一圆桌,周边有标号为1,2,3,4的四个座位,甲、乙、丙、丁四位同学坐在一起探讨一个数学课题,每人只能坐一个座位,甲先选座位,且甲、乙不能相邻,则所有选座方法有________种(用数字作答).
8
通过本节课,你学会了什么?
