人教版(2019)数学选择性必修三 6.3二项式定理课件(共23张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三 6.3二项式定理课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 884.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:27:55 | ||
图片预览








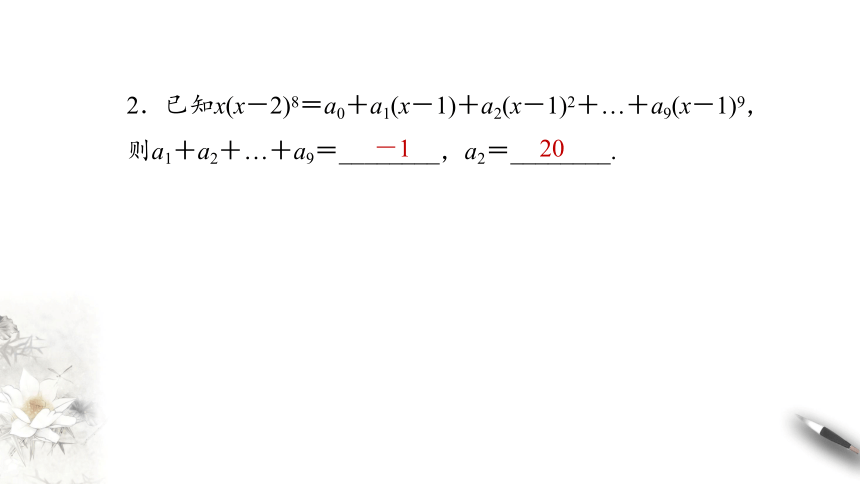
文档简介
(共23张PPT)
高二选择性必修三
二项式定理
新课程标准 考向预测 1.能用多项式运算法则和计数原理证明二项式定理. 2.会用二项式定理解决与二项展开式有关的简单问题. 命题角度 1.求二项展开式的特定项或系数
2.二项式系数与各项系数和问题
3.多项式的展开式问题
核心素养 数学运算、逻辑推理
基础梳理
基础点一 二项式定理
3.二项式系数
二项展开式中各项的系数为____________________.
(a+b)n=_________________________________________.
2.二项展开式的通项
Tr+1=Can-rbr,它表示第__________项.
an+ an-1b+…+ an-rbr+…+ bn
1.二项式定理
r+1
, , , ···,
解题时注意二项式系数中n和r的隐含条件.
使用二项式的通项时要注意:
(1)通项表示的是第r+1项,而不是第r项;
(2)通项中a和b的位置不能颠倒.
易错提醒
基础小测
(2019陕西西安西工大附中第一次月考)若的二项展开式中的x6的系数为9,则a=________.
1
性质 内容
对称性 与首末两端等距离的两个二项式系数相等,即_____________
增减性 当k<时,二项式系数逐渐增大
当k>时,二项式系数逐渐减小
最大值 当n是偶数时,中间一项的二项式系数最大,最大值为________;当n是奇数时,中间两项的二项式系数相等,且同时取得最大值,最大值为_________
二项式 系数的和 ++…++…+= ________;
+++…=+++…=_______
=
或
基础点二 二项式系数的性质
基础小测
1.(2020届山西高三开学考试)若的展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
A.210 B.180 C.160 D.175
B
2.已知x(x-2)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,则a1+a2+…+a9=________,a2=________.
-1
20
考点突破
考点一 二项展开式中的特定项或系数问题(高考热度:★★★★)
[例1] (x2+)5的展开式中x4的系数为( )
A.10 B.20
C.40 D.80
C
将上题改为(x2+ )5的展开式中x4的系数为40,则实数a的值为________.
同源变式
±2
通项公式法即利用二项展开式的通项公式,根据题意,对相应的指数进行赋值,从而解决指定项问题的方法.
此方法适用于已知二项式,求常数项、指定项的系数等问题.
破解此类题的关键点:
(1)求通项,根据二项式(a+b)n的展开式的通项Tk+1=an-kbk(k=
0,1,2,…,n),整理出Tk+1=m·xf(k).
(2)找方程,依题设条件中的指定项的相关信息,寻找关于k的方程.
(3)解方程,通过解方程,求出k的值.
(4)得结论,把k的值代入通项,得结论.
方法总结
考点微练
1.二项式(2x+1)6的展开式中,第5项的系数等于________.
60
2.(2019浙江卷,13)在二项式(+x)9的展开式中,常数项是________,系数为有理数的项的个数是________.
5
考点二 二项式系数的和与性质问题(高考热度:★★)
[例2] 若的展开式中各项系数之和为256,则n的值为________,展开式中的系数是________.
8
252
需要明确二项式系数与项的系数是完全不同的两个概念.
易错辨析
1.“赋值法”普遍运用于恒等式,是一种处理二项式相关问题比较常用的方法.对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R)的式子求其展开式各项系数之和,只需令x=1即可.
2.若f(x)=a0+a1x+a2x2+…+anxn,则f(x)的展开式中各项系数之和为f(1),奇数项系数之和为,偶数项系数之和为 .
归纳总结
1.(2019北京首都师范大学附属中学高三一模)若(x2+)n展开式中的二项式系数和为64,则n等于________,该展开式中的常数项为________.
6
15
考点微练
2.二项式(ax+ )n(a>0,b>0)的展开式中,设“所有二项式系数和”为A,“所有项的系数和”为B,“常数项”值为C,若A=B=256,C=70,则含x6的项为________.
8x6
考点三 多项式展开式中的特定项或系数问题(高考热度:★★★)
[例3] (2019全国卷Ⅲ,4) (1+2x2)(1+x)4的展开式中x3的系数为( )
A.12 B.16
C.20 D.24
A
1.几个多项式积的展开式中的特定项(系数)问题的处理方法:可先分别化简或展开为多项式和的形式,再分类考虑特定项产生的每一种情形,求出相应的特定项,最后进行合并即可.
归纳点拨
2.几个多项式和的展开式中特定项只需要先分别求出每一个多项式中的特定项,再合并即可.通常要用到方程或不等式的知识求解.
1.(2019广东深圳高级中学高三适应性考试)已知(1+)(2x-)5的展开式中各项系数的和为2,则该展开式中的常数项为( )
A.-80 B.-40 C.40 D.80
D
考点微练
根据题意给字母赋值是求解二项展开式各项系数和的一种重要方法.赋值法求展开式中的系数和或部分系数和,常赋的值为0,±1.
方法点拨
2.(1+)(1+x)6展开式中x2的系数为________.
30
通过本节课,你学会了什么?
高二选择性必修三
二项式定理
新课程标准 考向预测 1.能用多项式运算法则和计数原理证明二项式定理. 2.会用二项式定理解决与二项展开式有关的简单问题. 命题角度 1.求二项展开式的特定项或系数
2.二项式系数与各项系数和问题
3.多项式的展开式问题
核心素养 数学运算、逻辑推理
基础梳理
基础点一 二项式定理
3.二项式系数
二项展开式中各项的系数为____________________.
(a+b)n=_________________________________________.
2.二项展开式的通项
Tr+1=Can-rbr,它表示第__________项.
an+ an-1b+…+ an-rbr+…+ bn
1.二项式定理
r+1
, , , ···,
解题时注意二项式系数中n和r的隐含条件.
使用二项式的通项时要注意:
(1)通项表示的是第r+1项,而不是第r项;
(2)通项中a和b的位置不能颠倒.
易错提醒
基础小测
(2019陕西西安西工大附中第一次月考)若的二项展开式中的x6的系数为9,则a=________.
1
性质 内容
对称性 与首末两端等距离的两个二项式系数相等,即_____________
增减性 当k<时,二项式系数逐渐增大
当k>时,二项式系数逐渐减小
最大值 当n是偶数时,中间一项的二项式系数最大,最大值为________;当n是奇数时,中间两项的二项式系数相等,且同时取得最大值,最大值为_________
二项式 系数的和 ++…++…+= ________;
+++…=+++…=_______
=
或
基础点二 二项式系数的性质
基础小测
1.(2020届山西高三开学考试)若的展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
A.210 B.180 C.160 D.175
B
2.已知x(x-2)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,则a1+a2+…+a9=________,a2=________.
-1
20
考点突破
考点一 二项展开式中的特定项或系数问题(高考热度:★★★★)
[例1] (x2+)5的展开式中x4的系数为( )
A.10 B.20
C.40 D.80
C
将上题改为(x2+ )5的展开式中x4的系数为40,则实数a的值为________.
同源变式
±2
通项公式法即利用二项展开式的通项公式,根据题意,对相应的指数进行赋值,从而解决指定项问题的方法.
此方法适用于已知二项式,求常数项、指定项的系数等问题.
破解此类题的关键点:
(1)求通项,根据二项式(a+b)n的展开式的通项Tk+1=an-kbk(k=
0,1,2,…,n),整理出Tk+1=m·xf(k).
(2)找方程,依题设条件中的指定项的相关信息,寻找关于k的方程.
(3)解方程,通过解方程,求出k的值.
(4)得结论,把k的值代入通项,得结论.
方法总结
考点微练
1.二项式(2x+1)6的展开式中,第5项的系数等于________.
60
2.(2019浙江卷,13)在二项式(+x)9的展开式中,常数项是________,系数为有理数的项的个数是________.
5
考点二 二项式系数的和与性质问题(高考热度:★★)
[例2] 若的展开式中各项系数之和为256,则n的值为________,展开式中的系数是________.
8
252
需要明确二项式系数与项的系数是完全不同的两个概念.
易错辨析
1.“赋值法”普遍运用于恒等式,是一种处理二项式相关问题比较常用的方法.对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R)的式子求其展开式各项系数之和,只需令x=1即可.
2.若f(x)=a0+a1x+a2x2+…+anxn,则f(x)的展开式中各项系数之和为f(1),奇数项系数之和为,偶数项系数之和为 .
归纳总结
1.(2019北京首都师范大学附属中学高三一模)若(x2+)n展开式中的二项式系数和为64,则n等于________,该展开式中的常数项为________.
6
15
考点微练
2.二项式(ax+ )n(a>0,b>0)的展开式中,设“所有二项式系数和”为A,“所有项的系数和”为B,“常数项”值为C,若A=B=256,C=70,则含x6的项为________.
8x6
考点三 多项式展开式中的特定项或系数问题(高考热度:★★★)
[例3] (2019全国卷Ⅲ,4) (1+2x2)(1+x)4的展开式中x3的系数为( )
A.12 B.16
C.20 D.24
A
1.几个多项式积的展开式中的特定项(系数)问题的处理方法:可先分别化简或展开为多项式和的形式,再分类考虑特定项产生的每一种情形,求出相应的特定项,最后进行合并即可.
归纳点拨
2.几个多项式和的展开式中特定项只需要先分别求出每一个多项式中的特定项,再合并即可.通常要用到方程或不等式的知识求解.
1.(2019广东深圳高级中学高三适应性考试)已知(1+)(2x-)5的展开式中各项系数的和为2,则该展开式中的常数项为( )
A.-80 B.-40 C.40 D.80
D
考点微练
根据题意给字母赋值是求解二项展开式各项系数和的一种重要方法.赋值法求展开式中的系数和或部分系数和,常赋的值为0,±1.
方法点拨
2.(1+)(1+x)6展开式中x2的系数为________.
30
通过本节课,你学会了什么?
