人教版(2019)数学选择性必修三 7.2离散型随机变量及其分布列课件(共26张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三 7.2离散型随机变量及其分布列课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 652.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
高二选择性必修三
离散型随机变量及其分布列
新课程标准 考向预测 1.通过具体案例,了解离散型随机变量的概念,理解随机变量的分布列. 2.通过具体案例,了解超几何分布及其均值,并能解决简单的实际问题. 命题角度 1.求离散型的随机变量的分布列
2.超几何分布
核心素养 逻辑推理、数学运算
基础梳理
基础点一 离散型随机变量的概念与分布列
1.随机变量的有关概念
所有取值可以__________的随机变量.
随着试验结果变化而变化的变量,常用字母X,Y,ξ,η,…表示.
随机变量
离散型随机变量
一一列出
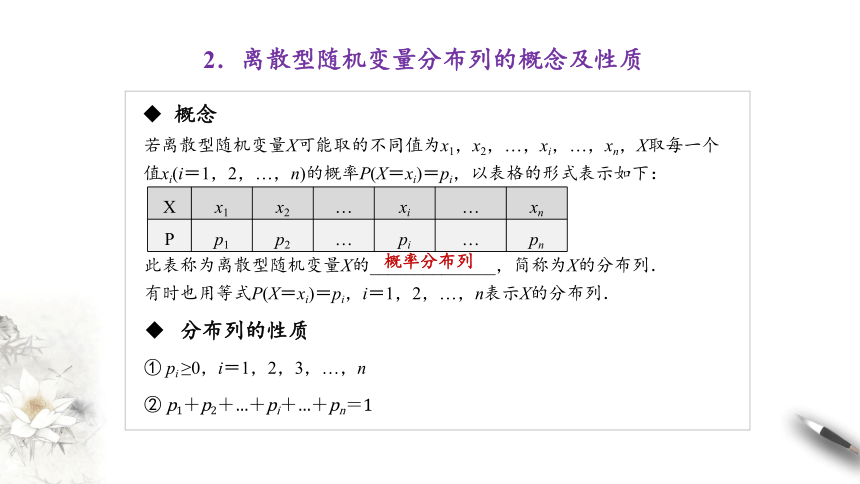
2.离散型随机变量分布列的概念及性质
若离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,以表格的形式表示如下:
概念
X x1 x2 … xi … xn
P p1 p2 … pi … pn
此表称为离散型随机变量X的______________,简称为X的分布列.
有时也用等式P(X=xi)=pi,i=1,2,…,n表示X的分布列.
概率分布列
分布列的性质
②
① pi ≥0,i=1,2,3,…,n
(1)对于分布列,易忽视其性质p1+p2+…+pn=1及pi≥0(i=1,2,…,n),其作用可用于检验所求离散型随机变量的分布列是否正确.
(2)确定离散型随机变量的取值时,易忽视各个可能取值表示的事件是彼此互斥的.
易错提醒
基础小测
1.抛掷甲、乙两枚骰子,所得点数之和为X,那么X=4表示的基本事件是( )
A.一枚是3点,一枚是1点
B.两枚都是2点
C.一枚是3点,一枚是1点或两枚都是2点
D.甲是3点,乙是1点或甲是1点,乙是3点或两枚都是2点
D
2.已知随机变量X的分布列为P(X=i)=(i=1,2,3),则P(X=2)=________.
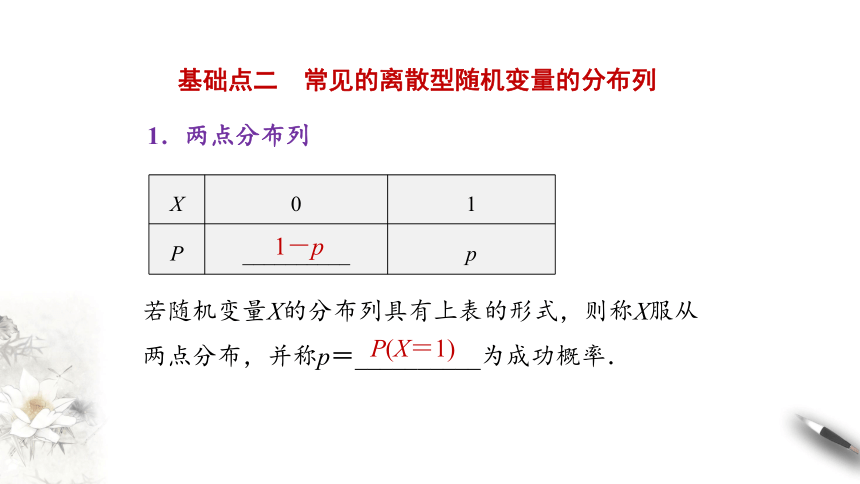
基础点二 常见的离散型随机变量的分布列
1.两点分布列
X 0 1
P __________ p
1-p
若随机变量X的分布列具有上表的形式,则称X服从两点分布,并称p=__________为成功概率.
P(X=1)
2.超几何分布列
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=,k=0,1,2,…,m,
其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*.
X 0 1 … m
P …
如果随机变量X的分布列具有上表的形式,那么称随机变量X服从____________.
超几何分布
基础小测
一盒中有12个乒乓球,其中9个新的、3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,则P(X=4)的值为( )
A. B. C. D.
C
考点突破
考点一 离散型随机变量分布列的性质(高考热度:★★)
[例1] 设随机变量ξ的概率分布列为P(ξ=k)=a ,其中k=0,1,2,则a=( )
A. B. C. D.
D
[例2] 设随机变量X的概率分布列为
X 1 2 3 4
P m
则P(|X-3|=1)=________.
(1)利用“总概率之和为1”可以求相关参数的取值范围或值;
(2)利用“离散型随机变量在一范围内的概率等于它取这个范围内各个值的概率之和”求某些特定事件的概率;
(3)可以根据性质判断所得分布列结果是否正确.
离散型随机变量的分布列的性质的应用
方法总结
考点二 离散型随机变量分布列的求法(高考热度:★★)
[例3] (2019广东高三3月一模)随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 男学员 女学员
第1次考科目二人数 1200 800
第1次通过科目二人数 960 600
第1次未通过科目二人数 240 200
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为X元,求X的分布列.
离散型随机变量分布列的求解步骤
方法总结
考点微练
(2019河南长垣一中高三检测)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为,,.
(1)设X表示一辆车从甲地到乙地遇到红灯的个数, 求随机变量X的分布列和数学期望;
(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
考点三 超几何分布(高考热度:★★)
[例4] 在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列.
变式1 用X表示接受乙种心理暗示的男志愿者人数,求X的分布列.
同源变式
变式2 用X表示接受乙种心理暗示的女志愿者人数与男志愿者人数之差,求X的分布列.
1.随机变量是否服从超几何分布的判断
若随机变量X服从超几何分布,则满足如下条件:
(1)该试验是不放回地抽取n次;
(2)随机变量X表示抽取到的次品件数(或类似事件),反之亦然.
解题技法
第一步,验证随机变量服从超几何分布,并确定参数N,M,n的值;
第二步,根据超几何分布的概率计算公式计算出随机变量取每一个值时的概率;
第三步,用表格的形式列出分布列.
2.求超几何分布的分布列的步骤
解题技法
考点微练
2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年~2016年中,我区城镇和农村人均住房建筑面积统计数据(单位:平方米).
2007年 2008年 2009年 2010年 2011年
城镇 18.66 20.25 22.79 25 27.1
农村 23.3 24.8 26.5 27.9 30.7
2012年 2013年 2014年 2015年 2016年
城镇 28.3 31.6 32.9 34.6 36.6
农村 32.4 34.1 37.1 41.2 45.8
(1)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2 平方米的概率;
(2)在给出的10年数据中,随机抽取三年,记X为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求X的分布列.
通过本节课,你学会了什么?
高二选择性必修三
离散型随机变量及其分布列
新课程标准 考向预测 1.通过具体案例,了解离散型随机变量的概念,理解随机变量的分布列. 2.通过具体案例,了解超几何分布及其均值,并能解决简单的实际问题. 命题角度 1.求离散型的随机变量的分布列
2.超几何分布
核心素养 逻辑推理、数学运算
基础梳理
基础点一 离散型随机变量的概念与分布列
1.随机变量的有关概念
所有取值可以__________的随机变量.
随着试验结果变化而变化的变量,常用字母X,Y,ξ,η,…表示.
随机变量
离散型随机变量
一一列出
2.离散型随机变量分布列的概念及性质
若离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,以表格的形式表示如下:
概念
X x1 x2 … xi … xn
P p1 p2 … pi … pn
此表称为离散型随机变量X的______________,简称为X的分布列.
有时也用等式P(X=xi)=pi,i=1,2,…,n表示X的分布列.
概率分布列
分布列的性质
②
① pi ≥0,i=1,2,3,…,n
(1)对于分布列,易忽视其性质p1+p2+…+pn=1及pi≥0(i=1,2,…,n),其作用可用于检验所求离散型随机变量的分布列是否正确.
(2)确定离散型随机变量的取值时,易忽视各个可能取值表示的事件是彼此互斥的.
易错提醒
基础小测
1.抛掷甲、乙两枚骰子,所得点数之和为X,那么X=4表示的基本事件是( )
A.一枚是3点,一枚是1点
B.两枚都是2点
C.一枚是3点,一枚是1点或两枚都是2点
D.甲是3点,乙是1点或甲是1点,乙是3点或两枚都是2点
D
2.已知随机变量X的分布列为P(X=i)=(i=1,2,3),则P(X=2)=________.
基础点二 常见的离散型随机变量的分布列
1.两点分布列
X 0 1
P __________ p
1-p
若随机变量X的分布列具有上表的形式,则称X服从两点分布,并称p=__________为成功概率.
P(X=1)
2.超几何分布列
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=,k=0,1,2,…,m,
其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*.
X 0 1 … m
P …
如果随机变量X的分布列具有上表的形式,那么称随机变量X服从____________.
超几何分布
基础小测
一盒中有12个乒乓球,其中9个新的、3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,则P(X=4)的值为( )
A. B. C. D.
C
考点突破
考点一 离散型随机变量分布列的性质(高考热度:★★)
[例1] 设随机变量ξ的概率分布列为P(ξ=k)=a ,其中k=0,1,2,则a=( )
A. B. C. D.
D
[例2] 设随机变量X的概率分布列为
X 1 2 3 4
P m
则P(|X-3|=1)=________.
(1)利用“总概率之和为1”可以求相关参数的取值范围或值;
(2)利用“离散型随机变量在一范围内的概率等于它取这个范围内各个值的概率之和”求某些特定事件的概率;
(3)可以根据性质判断所得分布列结果是否正确.
离散型随机变量的分布列的性质的应用
方法总结
考点二 离散型随机变量分布列的求法(高考热度:★★)
[例3] (2019广东高三3月一模)随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 男学员 女学员
第1次考科目二人数 1200 800
第1次通过科目二人数 960 600
第1次未通过科目二人数 240 200
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为X元,求X的分布列.
离散型随机变量分布列的求解步骤
方法总结
考点微练
(2019河南长垣一中高三检测)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为,,.
(1)设X表示一辆车从甲地到乙地遇到红灯的个数, 求随机变量X的分布列和数学期望;
(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
考点三 超几何分布(高考热度:★★)
[例4] 在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列.
变式1 用X表示接受乙种心理暗示的男志愿者人数,求X的分布列.
同源变式
变式2 用X表示接受乙种心理暗示的女志愿者人数与男志愿者人数之差,求X的分布列.
1.随机变量是否服从超几何分布的判断
若随机变量X服从超几何分布,则满足如下条件:
(1)该试验是不放回地抽取n次;
(2)随机变量X表示抽取到的次品件数(或类似事件),反之亦然.
解题技法
第一步,验证随机变量服从超几何分布,并确定参数N,M,n的值;
第二步,根据超几何分布的概率计算公式计算出随机变量取每一个值时的概率;
第三步,用表格的形式列出分布列.
2.求超几何分布的分布列的步骤
解题技法
考点微练
2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年~2016年中,我区城镇和农村人均住房建筑面积统计数据(单位:平方米).
2007年 2008年 2009年 2010年 2011年
城镇 18.66 20.25 22.79 25 27.1
农村 23.3 24.8 26.5 27.9 30.7
2012年 2013年 2014年 2015年 2016年
城镇 28.3 31.6 32.9 34.6 36.6
农村 32.4 34.1 37.1 41.2 45.8
(1)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2 平方米的概率;
(2)在给出的10年数据中,随机抽取三年,记X为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求X的分布列.
通过本节课,你学会了什么?
