人教版(2019)数学选择性必修三 7.3.2离散型随机变量的方差课件(共24张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三 7.3.2离散型随机变量的方差课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 685.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
7.3.2 离散型随机变量的方差
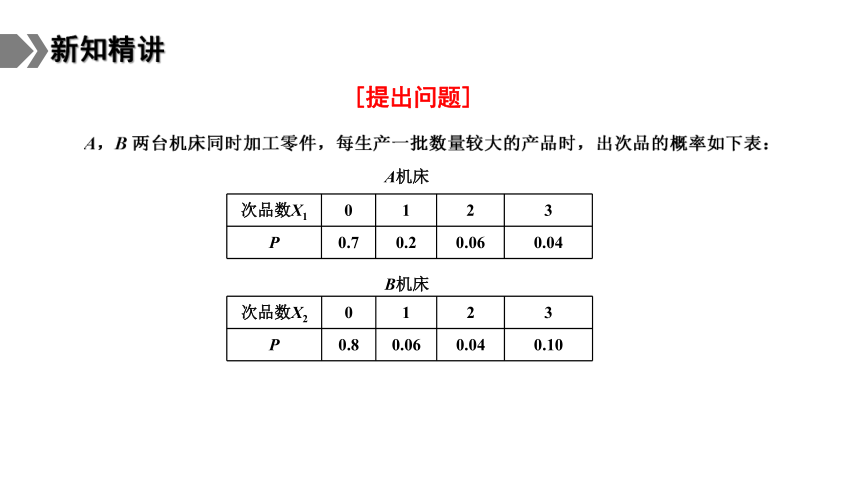
[提出问题]
A机床
次品数X1 0 1 2 3
P 0.7 0.2 0.06 0.04
B机床
次品数X2 0 1 2 3
P 0.8 0.06 0.04 0.10
新知精讲
新知精讲
[导入新知]
新知精讲
越小
越小
新知精讲
新知精讲
新知精讲
[化解疑难]
典例剖析
题型一 求离散型随机变量的方差
[例1] 袋中有大小相同的小球6个,其中红球2个、黄球4个,规定取1个红球得2分,1个黄球得1分.从袋中任取3个小球,记所取3个小球的分数之和为X,求随机变量X的分布列、均值和方差.
典例剖析
[类题通法]
1.离散型随机变量的分布列、均值和方差是三个紧密联系的有机统一体,一般在试题中综合在一起考查,其关键是求出分布列.
2.在求分布列时,要注意利用等可能事件、互斥事件,相互独立事件的概率公式计算概率,并注意结合分布列的性质,简化概率计算.
活学活用
典例剖析
题型二 求两点分布、二项分布的方差、标准差
典例剖析
[类题通法]
解此类问题,首先要确定正确的离散型随机变量,然后确定它是否服从特殊分布,若它服从两点分布,则其方差为p(1-p);若其服从二项分布,则其方差为np(1-p)(其中p为成功概率).
活学活用
典例剖析
题型三 离散型随机变量的均值、方差的实际应用
ξ 10 9 8 7
P 0.5 0.3 0.1 0.1
η 10 9 8 7
P 0.3 0.3 0.2 0.2
典例剖析
题型三 离散型随机变量的均值、方差的实际应用
典例剖析
[类题通法]
数学期望体现了随机变量取值的平均大小,但有时仅知道均值大小是不够的,比如:两个随机变量的均值相等(即数学期望相等),这时还需要知道随机变量的取值如何在均值附近变化,即计算其方差,方差大说明随机变量取值比较分散;方差小说明随机变量的取值比较集中、稳定.
X 0 1 2 3
P 0.3 0.3 0.2 0.2
乙保护区:
Y 0 1 2
P 0.1 0.5 0.4
试评定这两个保护区的管理水平.
活学活用
因为E(X)=E(Y),D(X)>D(Y),所以两个保护区内每季度发生的平均违规次数是相同的,但乙保护区内的违规事件次数更集中和稳定,而甲保护区的违规事件次数相对分散,故乙保护区的管理水平较高.
A
随堂检测
D
随堂检测
随堂检测
在均值相等的情况下,方差越小,说明包装的质量越稳定,所以自动包装机乙的质量较好.
乙
随堂检测
随堂检测
5.已知某运动员投篮命中率p=0.6,
(1)求一次投篮命中次数ξ的均值与方差;
(2)求重复5次投篮时,命中次数η的均值与方差.
随堂检测
5.已知某运动员投篮命中率p=0.6,
(1)求一次投篮命中次数ξ的均值与方差;
(2)求重复5次投篮时,命中次数η的均值与方差.
再见
7.3.2 离散型随机变量的方差
[提出问题]
A机床
次品数X1 0 1 2 3
P 0.7 0.2 0.06 0.04
B机床
次品数X2 0 1 2 3
P 0.8 0.06 0.04 0.10
新知精讲
新知精讲
[导入新知]
新知精讲
越小
越小
新知精讲
新知精讲
新知精讲
[化解疑难]
典例剖析
题型一 求离散型随机变量的方差
[例1] 袋中有大小相同的小球6个,其中红球2个、黄球4个,规定取1个红球得2分,1个黄球得1分.从袋中任取3个小球,记所取3个小球的分数之和为X,求随机变量X的分布列、均值和方差.
典例剖析
[类题通法]
1.离散型随机变量的分布列、均值和方差是三个紧密联系的有机统一体,一般在试题中综合在一起考查,其关键是求出分布列.
2.在求分布列时,要注意利用等可能事件、互斥事件,相互独立事件的概率公式计算概率,并注意结合分布列的性质,简化概率计算.
活学活用
典例剖析
题型二 求两点分布、二项分布的方差、标准差
典例剖析
[类题通法]
解此类问题,首先要确定正确的离散型随机变量,然后确定它是否服从特殊分布,若它服从两点分布,则其方差为p(1-p);若其服从二项分布,则其方差为np(1-p)(其中p为成功概率).
活学活用
典例剖析
题型三 离散型随机变量的均值、方差的实际应用
ξ 10 9 8 7
P 0.5 0.3 0.1 0.1
η 10 9 8 7
P 0.3 0.3 0.2 0.2
典例剖析
题型三 离散型随机变量的均值、方差的实际应用
典例剖析
[类题通法]
数学期望体现了随机变量取值的平均大小,但有时仅知道均值大小是不够的,比如:两个随机变量的均值相等(即数学期望相等),这时还需要知道随机变量的取值如何在均值附近变化,即计算其方差,方差大说明随机变量取值比较分散;方差小说明随机变量的取值比较集中、稳定.
X 0 1 2 3
P 0.3 0.3 0.2 0.2
乙保护区:
Y 0 1 2
P 0.1 0.5 0.4
试评定这两个保护区的管理水平.
活学活用
因为E(X)=E(Y),D(X)>D(Y),所以两个保护区内每季度发生的平均违规次数是相同的,但乙保护区内的违规事件次数更集中和稳定,而甲保护区的违规事件次数相对分散,故乙保护区的管理水平较高.
A
随堂检测
D
随堂检测
随堂检测
在均值相等的情况下,方差越小,说明包装的质量越稳定,所以自动包装机乙的质量较好.
乙
随堂检测
随堂检测
5.已知某运动员投篮命中率p=0.6,
(1)求一次投篮命中次数ξ的均值与方差;
(2)求重复5次投篮时,命中次数η的均值与方差.
随堂检测
5.已知某运动员投篮命中率p=0.6,
(1)求一次投篮命中次数ξ的均值与方差;
(2)求重复5次投篮时,命中次数η的均值与方差.
再见
