人教版(2019)数学选择性必修三 第六章计数原理章末复习课件(共42张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三 第六章计数原理章末复习课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:38:29 | ||
图片预览











文档简介
(共42张PPT)
计数原理 章末复习
高二
选择性必修三
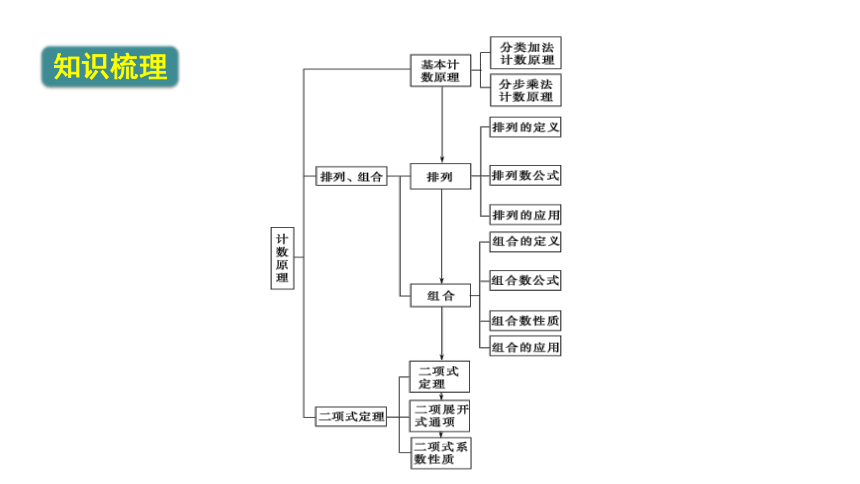
知识梳理
完成一件事可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,…,在第n类办法中有mn种不同的方法,那么完成这件事共有N=_________________种不同的方法.
m1+m2+…+mn
完成一件事需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事有N=___________________种不同的方法.
m1×m2×…×mn
1.分类加法计数原理
2.分步乘法计数原理
考点复习
3.排列数与组合数公式及性质
4. 二项式定理
(1)二项式定理的内容
(2)通项公式
4. 二项式定理
专题探究一 两个计数原理
分类加法计数原理和分步乘法计数原理是本部分内容的基础,经常要对问题进行分类或者分步进行分析求解.
(1)“分类”表现为其中任何一类均可独立完成所给事情.“分步”表现为必须把各步骤均完成,才能完成所给事情.
(2)分类加法计数原理强调完成一件事情的几类办法互不干扰,不论哪一类办法中的哪一种方法都能够独立完成事件.
分步乘法计数原理强调各步骤缺一不可,需要依次完成所有步骤才能完成事件,步与步之间互不影响,即前一步用什么方法不影响后一步采取什么方法.
例1 (1)方程=1表示焦点在y轴上的椭圆,其中m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},那么这样的椭圆的个数是________.
20
以m的值为标准分类,分五类:
第一类:m=1时,使n>m,n有6种选择;
第二类:m=2时,使n>m,n有5种选择;
第三类:n=3时,使n>m,n有4种选择;
第四类:n=4时,使n>m,n有3种选择;
第五类:n=5时,使n>m,n有2种选择;
所以共有6+5+4+3+2=20种方法.
(2)某电视台连续播放6个广告,其中有3个不同的商业广告、两个不同的宣传广告、一个公益广告,要求最后播放的不能是商业广告,且宣传广告与公益广告不能连续播放,两个宣传广告也不能连续播放,则有多少种不同的播放方式?
用1,2,3,4,5,6表示广告的播放顺序,则完成这件事有三类方法.
第一类:宣传广告与公益广告的播放顺序是2,4,6.
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
第二类:宣传广告与公益广告的播放顺序是1,4,6,
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
第三类:宣传广告与公益广告的播放顺序是1,3,6,
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
由分类加法计数原理得:6个广告不同的播放方式有36+36+36=108种.
方程=1表示焦点在x轴上的椭圆,其中m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},那么这样的椭圆的个数是________.
延伸探究
10
由题意知m>n>0,以m的取值进行分类.
当m=1时,n值不存在;
当m=2时,n可取1,只有1种选择;
当m=3时,n可取1,2,有2种选择;
当m=4时,n可取1,2,3,有3种选择;
当m=5时,n可取1,2,3,4,有4种选择;
由分类加法计数原理可知,符合条件的椭圆共有10个.
规律方法
1.使用两个原理解决问题的思路
(1) 根据完成某件事情的方式,确定是分类还是分步,要抓住两个原理的本质.
(2)分类加法计数原理的关键是“类”,分类时,首先要根据问题的特点确定一个合适的分类标准,然后在这个标准下进行分类;其次分类时要注意,完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法.
(3)分步乘法计数原理的关键是“步”,分步时首先要根据问题的特点确定一个分步的标准;其次,分步时还要注意满足完成一件事必须并且只有连续完成这n个步骤后,这件事才算完成,只有满足了上述条件,才能用分步乘法计数原理.
规律方法
2.使用两个原理解决问题时应注意的问题
对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(1)每人恰好参加一项,每项人数不限;
每人都可以从这三个比赛项目中选报一项,各有3种不同选法,由分步乘法计数原理,知共有选法36=729(种).
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(2)每项限报一人,且每人至多参加一项;
每项限报一人,且每人至多参加一项,因此可由项目选人,
第一个项目有6种选法,
第二个项目有5种选法,
第三个项目只有4种选法,
由分步乘法计数原理,得共有报名方法6×5×4=120(种).
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(3)每项限报一人,但每人参加的项目不限.
由于每人参加的项目不限,因此每一个项目都可以从这六人中选出一人参赛,由分步乘法计数原理,得共有不同的报名方法63=216(种).
专题探究二 排列、组合的应用
例2 (1)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员且1、2号中至少有1名新队员的排法有________种.(用数字作答)
48
①只有1名老队员的排法有=36种.
②有2名老队员的排法有=12种.
所以共有36+12=48种.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
①当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
根据分步乘法计数原理,一共有5040×24=120960种.
捆绑法
第一步,先将4个舞蹈节目捆绑起来,看成1个节目,
与6个演唱节目一起排,有=5040种方法;
第二步,再松绑,给4个节目排序,有=24种方法.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
②当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
第一步,将6个演唱节目排成一列(如下图中的“□”),一共有=720种方法.
×□×□×□×□×□×□×
第二步,再将4个舞蹈节目排在一头一尾或两个节目中间(即图中“×”的位置),
这样相当于7个“×”选4个来排,一共有=7×6×5×4=840种.
根据分步乘法计数原理,一共有720×840=604800种.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
③若已定好节目单,后来情况有变,需加上诗朗诵和快板2个栏目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
若所有节目没有顺序要求,全部排列,则有种排法,
但原来的节目已定好顺序,需要消除,
所以节目演出的方式有= =132种排法.
规律方法
1.处理排列组合应用题的一般步骤
(1)认真审题,弄清楚是排列(有序)还是组合(无序),还是排列与组合混合问题.
(2)抓住问题的本质特征,准确合理地利用两个基本原理进行“分类与分步”.
规律方法
2.处理排列组合应用题的规律
(1)两种思路:直接法,间接法.
(2)两种途径:元素分析法,位置分析法.
规律方法
3.排列组合应用题的常见类型和解决方法
(1)特殊元素、特殊位置优先安排的策略.
(2)合理分类与准确分步的策略.
(3)正难则反,等价转化的策略.
(4)相邻问题捆绑法,不相邻问题插空法的策略.
(5)元素定序,先排后除的策略.
(6)排列、组合混合题先选后排策略.
(7)复杂问题构造模型策略.
跟踪训练
2.(1)我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
A.12种 B.18种 C.24种 D.48种
C
法一
将甲、乙两机“捆绑”看作一个元素,与除去丙、丁两机外的另一架飞机进行全排列,再将丙、丁两机“插空”排入,
共有· · =24种不同着舰方法.
跟踪训练
2.(1)我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
A.12种 B.18种 C.24种 D.48种
C
法二
先对甲、乙两机“捆绑”在一起看作整体,该整体有两种着舰方法,此时相当于只有4架舰载机,这4架舰载机有种着舰方法,其中有· 种方法丙丁两机相邻着舰,利用分步乘法计数原理得2×()=24种.
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
①3名教师必须排在一起的不同排法有多少种?
3名教师的排法有,把3名教师作为一个整体与4个学生共5个元素的全排列共有种,则共有=720(种).
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
②3名教师必须在中间(在3,4,5位置上)的不同排法有多少种?
3名教师的排法有,
4个学生在4个位子上的全排列共有种,
则共有=144(种).
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
③3名教师不能相邻的不同排法有多少种?
先4个学生全排列,
再在五个空位中任选3个排3名教师,
共=1440(种).
专题探究三 二项式定理的应用
通项公式Tr+1= an-rbr(r=0,1,2,…,n)集中体现了二项展开式中的指数、项数、系数的变化,是二项式定理的核心,它在求展开式的某些特定项(如含指定幂的项、常数项、中间项、有理项、系数最大的项等)及其系数等方面有着广泛的应用.
例3 (1)已知(1+kx2)6(k是正整数)的展开式中x8的系数小于120,则k=________.
专题探究三 二项式定理的应用
1
(1+kx2)6的展开式的通项为Tr+1= (kx2)r= krx2r,
令2r=8得r=4,
∴x8的系数为·k4=15k4
∴15k4<120.也即k4<8,
又k是正整数.故k只能取1.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
①求n;
令x=1得二项式展开式中各项系数之和为(5-1)n=4n,
各项二项式系数之和为2n,
由题意得,4n=16·2n,
所以2n=16,n=4.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
②求展开式中二项式系数最大的项;
通项Tr+1= (5x)4-r =(-1)r 54-r .
展开式中二项式系数最大的项是第3项:
T3=(-1)2 52x=150x.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
③求展开式中所有x的有理项.
由②得:4- r∈Z.(r=0,1,2,3,4),即r=0,2,4,
所以展开式中所有x的有理项为
T1=(-1)0 54x4=625x4,
T3=(-1)2 52x=150x,
T5=(-1)4 50x-2=x-2.
规律方法
应用二项式定理解题要注意的问题
(1)通项公式表示的是第“r+1”项,而不是第“r”项.
(2)展开式中第r+1项的二项式系数与第r+1项的系数,在一般情况下是不相同的,在具体求各项的系数时,一般先处理符号,对根式和指数的运算要细心,以防出差错.
(3)它表示二项展开式中的任意项,只要n与r确定,该项也随之确定.对于一个具体的二项式,它的展开式中的项Tr+1依赖于r.
3.(1)若二项式的展开式中的系数是84,则实数a=( )
A.2 B. C.1 D.
跟踪训练
C
二项式的展开式的通项公式为
Tr+1= (2x)7-r = 27-rarx7-2r,
令7-2r=-3,得r=5.
故展开式中的系数是22a5=84,解得a=1.
(2)已知(n∈N*)的展开式中没有常数项,且2≤n≤8,
则n=________.
跟踪训练
5
展开式的通项是Tr+1= xn-r = xn-4r,r=0,1,2,…,n,
由于的展开式中没有常数项,
所以xn-4r,x xn-4r= xn-4r+1和x2xn-4r=xn-4r+2都不是常数,
则n-4r≠0,n-4r+1≠0,n-4r+2≠0,
又因为2≤n≤8,所以n≠2,3,4,6,7,8,故取n=5.
专题探究四 二项式定理中的“赋值” 问题
例4 (1)若(x2+1)(x-3)9=a0+a1(x-2)+a2(x-2)2+a3(x-2)3+…+a11(x-2)11,则a1+a2+a3+…+a11的值为________.
5
对已知条件式中令x=2,
得a0=(4+1)×(-1)=-5;
令x=3得a0+a1+a2+…+a11=(9+1)×0=0;
∴a1+a2+a3+…+a11=5.
专题探究四 二项式定理中的“赋值” 问题
①a0.
②a1+a2+a3+a4+…+a100.
令x=0,则展开式为a0=2100.
③a1+a3+a5+…+a99.
所以a1+a2+…+a100=(2- )100-2100.
令x=1,可得a0+a1+a2+…+a100=(2- )100
(*)
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
令x=-1,可得a0-a1+a2-a3+…+a100=(2+ )100.
与②中(*)式联立相减得
a1+a3+…+a99= .
专题探究四 二项式定理中的“赋值” 问题
④(a0+a2+…+a100)2-(a1+a3+…+a99)2.
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
原式=[(a0+a2+…+a100)+(a1+a3+…+a99)][(a0+a2+…+a100)-(a1+a3+…+a99)]
=(a0+a1+a2+…+a100)·(a0-a1+a2-a3+…+a98-a99+a100)
=[(2-)(2+)]100
=1100
=1.
专题探究四 二项式定理中的“赋值” 问题
⑤|a0|+|a1|+…+|a100|.
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
因为Tr+1=(-1)r2100-r()rxr,
所以a2k-1<0(k∈N+).
所以|a0|+|a1|+|a2|+…+|a100|
=a0-a1+a2-a3+…+a100
=(2+ )100.
规律方法
赋值法的应用规律
与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和,主要方法是赋值法,通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
提醒:求各项系数的绝对值的和时,要先根据绝对值里面数的符号赋值求解.
跟踪训练
4.(1)已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn.若a1+a2+…+an-1=29-n,那么自然数n的值为( )
A.6 B.5 C.4 D.3
C
令x=1得2+22+23+…+2n=a0+a1+a2+…+an
即=a0+a1+a2+…+an,
即2n+1-2=a0+a1+a2+…+an
令x=0得a0=1+1+1+…+1=n,
∵an=1,∴a1+a2+…+an-1=2n+1-n-3,
∴2n+1-n-3=29-n,解得n=4.
跟踪训练
(2)若(1+x+x2)6=a0+a1x+a2x2+…+a12x12,则a2+a4+…+a12=________.
令x=0得,a0=1.
∴当x=1时,a0+a1+a2+…+a11+a12=36;①
当x=-1时,a0-a1+a2+…-a11+a12=1;②
①+②得2(a0+a2+a4+…+a12)=730,
∴a2+a4+a6+…+a12=364.
364
计数原理 章末复习
高二
选择性必修三
知识梳理
完成一件事可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,…,在第n类办法中有mn种不同的方法,那么完成这件事共有N=_________________种不同的方法.
m1+m2+…+mn
完成一件事需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事有N=___________________种不同的方法.
m1×m2×…×mn
1.分类加法计数原理
2.分步乘法计数原理
考点复习
3.排列数与组合数公式及性质
4. 二项式定理
(1)二项式定理的内容
(2)通项公式
4. 二项式定理
专题探究一 两个计数原理
分类加法计数原理和分步乘法计数原理是本部分内容的基础,经常要对问题进行分类或者分步进行分析求解.
(1)“分类”表现为其中任何一类均可独立完成所给事情.“分步”表现为必须把各步骤均完成,才能完成所给事情.
(2)分类加法计数原理强调完成一件事情的几类办法互不干扰,不论哪一类办法中的哪一种方法都能够独立完成事件.
分步乘法计数原理强调各步骤缺一不可,需要依次完成所有步骤才能完成事件,步与步之间互不影响,即前一步用什么方法不影响后一步采取什么方法.
例1 (1)方程=1表示焦点在y轴上的椭圆,其中m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},那么这样的椭圆的个数是________.
20
以m的值为标准分类,分五类:
第一类:m=1时,使n>m,n有6种选择;
第二类:m=2时,使n>m,n有5种选择;
第三类:n=3时,使n>m,n有4种选择;
第四类:n=4时,使n>m,n有3种选择;
第五类:n=5时,使n>m,n有2种选择;
所以共有6+5+4+3+2=20种方法.
(2)某电视台连续播放6个广告,其中有3个不同的商业广告、两个不同的宣传广告、一个公益广告,要求最后播放的不能是商业广告,且宣传广告与公益广告不能连续播放,两个宣传广告也不能连续播放,则有多少种不同的播放方式?
用1,2,3,4,5,6表示广告的播放顺序,则完成这件事有三类方法.
第一类:宣传广告与公益广告的播放顺序是2,4,6.
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
第二类:宣传广告与公益广告的播放顺序是1,4,6,
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
第三类:宣传广告与公益广告的播放顺序是1,3,6,
分6步完成这件事,共有3×3×2×2×1×1=36种不同的播放方式.
由分类加法计数原理得:6个广告不同的播放方式有36+36+36=108种.
方程=1表示焦点在x轴上的椭圆,其中m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},那么这样的椭圆的个数是________.
延伸探究
10
由题意知m>n>0,以m的取值进行分类.
当m=1时,n值不存在;
当m=2时,n可取1,只有1种选择;
当m=3时,n可取1,2,有2种选择;
当m=4时,n可取1,2,3,有3种选择;
当m=5时,n可取1,2,3,4,有4种选择;
由分类加法计数原理可知,符合条件的椭圆共有10个.
规律方法
1.使用两个原理解决问题的思路
(1) 根据完成某件事情的方式,确定是分类还是分步,要抓住两个原理的本质.
(2)分类加法计数原理的关键是“类”,分类时,首先要根据问题的特点确定一个合适的分类标准,然后在这个标准下进行分类;其次分类时要注意,完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法.
(3)分步乘法计数原理的关键是“步”,分步时首先要根据问题的特点确定一个分步的标准;其次,分步时还要注意满足完成一件事必须并且只有连续完成这n个步骤后,这件事才算完成,只有满足了上述条件,才能用分步乘法计数原理.
规律方法
2.使用两个原理解决问题时应注意的问题
对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(1)每人恰好参加一项,每项人数不限;
每人都可以从这三个比赛项目中选报一项,各有3种不同选法,由分步乘法计数原理,知共有选法36=729(种).
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(2)每项限报一人,且每人至多参加一项;
每项限报一人,且每人至多参加一项,因此可由项目选人,
第一个项目有6种选法,
第二个项目有5种选法,
第三个项目只有4种选法,
由分步乘法计数原理,得共有报名方法6×5×4=120(种).
跟踪训练
1.有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(3)每项限报一人,但每人参加的项目不限.
由于每人参加的项目不限,因此每一个项目都可以从这六人中选出一人参赛,由分步乘法计数原理,得共有不同的报名方法63=216(种).
专题探究二 排列、组合的应用
例2 (1)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员且1、2号中至少有1名新队员的排法有________种.(用数字作答)
48
①只有1名老队员的排法有=36种.
②有2名老队员的排法有=12种.
所以共有36+12=48种.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
①当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
根据分步乘法计数原理,一共有5040×24=120960种.
捆绑法
第一步,先将4个舞蹈节目捆绑起来,看成1个节目,
与6个演唱节目一起排,有=5040种方法;
第二步,再松绑,给4个节目排序,有=24种方法.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
②当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
第一步,将6个演唱节目排成一列(如下图中的“□”),一共有=720种方法.
×□×□×□×□×□×□×
第二步,再将4个舞蹈节目排在一头一尾或两个节目中间(即图中“×”的位置),
这样相当于7个“×”选4个来排,一共有=7×6×5×4=840种.
根据分步乘法计数原理,一共有720×840=604800种.
专题探究二 排列、组合的应用
(2)在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
③若已定好节目单,后来情况有变,需加上诗朗诵和快板2个栏目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
若所有节目没有顺序要求,全部排列,则有种排法,
但原来的节目已定好顺序,需要消除,
所以节目演出的方式有= =132种排法.
规律方法
1.处理排列组合应用题的一般步骤
(1)认真审题,弄清楚是排列(有序)还是组合(无序),还是排列与组合混合问题.
(2)抓住问题的本质特征,准确合理地利用两个基本原理进行“分类与分步”.
规律方法
2.处理排列组合应用题的规律
(1)两种思路:直接法,间接法.
(2)两种途径:元素分析法,位置分析法.
规律方法
3.排列组合应用题的常见类型和解决方法
(1)特殊元素、特殊位置优先安排的策略.
(2)合理分类与准确分步的策略.
(3)正难则反,等价转化的策略.
(4)相邻问题捆绑法,不相邻问题插空法的策略.
(5)元素定序,先排后除的策略.
(6)排列、组合混合题先选后排策略.
(7)复杂问题构造模型策略.
跟踪训练
2.(1)我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
A.12种 B.18种 C.24种 D.48种
C
法一
将甲、乙两机“捆绑”看作一个元素,与除去丙、丁两机外的另一架飞机进行全排列,再将丙、丁两机“插空”排入,
共有· · =24种不同着舰方法.
跟踪训练
2.(1)我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
A.12种 B.18种 C.24种 D.48种
C
法二
先对甲、乙两机“捆绑”在一起看作整体,该整体有两种着舰方法,此时相当于只有4架舰载机,这4架舰载机有种着舰方法,其中有· 种方法丙丁两机相邻着舰,利用分步乘法计数原理得2×()=24种.
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
①3名教师必须排在一起的不同排法有多少种?
3名教师的排法有,把3名教师作为一个整体与4个学生共5个元素的全排列共有种,则共有=720(种).
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
②3名教师必须在中间(在3,4,5位置上)的不同排法有多少种?
3名教师的排法有,
4个学生在4个位子上的全排列共有种,
则共有=144(种).
跟踪训练
(2)3名教师与4名学生排成一横排照相,求
③3名教师不能相邻的不同排法有多少种?
先4个学生全排列,
再在五个空位中任选3个排3名教师,
共=1440(种).
专题探究三 二项式定理的应用
通项公式Tr+1= an-rbr(r=0,1,2,…,n)集中体现了二项展开式中的指数、项数、系数的变化,是二项式定理的核心,它在求展开式的某些特定项(如含指定幂的项、常数项、中间项、有理项、系数最大的项等)及其系数等方面有着广泛的应用.
例3 (1)已知(1+kx2)6(k是正整数)的展开式中x8的系数小于120,则k=________.
专题探究三 二项式定理的应用
1
(1+kx2)6的展开式的通项为Tr+1= (kx2)r= krx2r,
令2r=8得r=4,
∴x8的系数为·k4=15k4
∴15k4<120.也即k4<8,
又k是正整数.故k只能取1.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
①求n;
令x=1得二项式展开式中各项系数之和为(5-1)n=4n,
各项二项式系数之和为2n,
由题意得,4n=16·2n,
所以2n=16,n=4.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
②求展开式中二项式系数最大的项;
通项Tr+1= (5x)4-r =(-1)r 54-r .
展开式中二项式系数最大的项是第3项:
T3=(-1)2 52x=150x.
专题探究三 二项式定理的应用
例3 (2)已知二项式展开式中各项系数之和是各项二项式系数之和的16倍.
③求展开式中所有x的有理项.
由②得:4- r∈Z.(r=0,1,2,3,4),即r=0,2,4,
所以展开式中所有x的有理项为
T1=(-1)0 54x4=625x4,
T3=(-1)2 52x=150x,
T5=(-1)4 50x-2=x-2.
规律方法
应用二项式定理解题要注意的问题
(1)通项公式表示的是第“r+1”项,而不是第“r”项.
(2)展开式中第r+1项的二项式系数与第r+1项的系数,在一般情况下是不相同的,在具体求各项的系数时,一般先处理符号,对根式和指数的运算要细心,以防出差错.
(3)它表示二项展开式中的任意项,只要n与r确定,该项也随之确定.对于一个具体的二项式,它的展开式中的项Tr+1依赖于r.
3.(1)若二项式的展开式中的系数是84,则实数a=( )
A.2 B. C.1 D.
跟踪训练
C
二项式的展开式的通项公式为
Tr+1= (2x)7-r = 27-rarx7-2r,
令7-2r=-3,得r=5.
故展开式中的系数是22a5=84,解得a=1.
(2)已知(n∈N*)的展开式中没有常数项,且2≤n≤8,
则n=________.
跟踪训练
5
展开式的通项是Tr+1= xn-r = xn-4r,r=0,1,2,…,n,
由于的展开式中没有常数项,
所以xn-4r,x xn-4r= xn-4r+1和x2xn-4r=xn-4r+2都不是常数,
则n-4r≠0,n-4r+1≠0,n-4r+2≠0,
又因为2≤n≤8,所以n≠2,3,4,6,7,8,故取n=5.
专题探究四 二项式定理中的“赋值” 问题
例4 (1)若(x2+1)(x-3)9=a0+a1(x-2)+a2(x-2)2+a3(x-2)3+…+a11(x-2)11,则a1+a2+a3+…+a11的值为________.
5
对已知条件式中令x=2,
得a0=(4+1)×(-1)=-5;
令x=3得a0+a1+a2+…+a11=(9+1)×0=0;
∴a1+a2+a3+…+a11=5.
专题探究四 二项式定理中的“赋值” 问题
①a0.
②a1+a2+a3+a4+…+a100.
令x=0,则展开式为a0=2100.
③a1+a3+a5+…+a99.
所以a1+a2+…+a100=(2- )100-2100.
令x=1,可得a0+a1+a2+…+a100=(2- )100
(*)
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
令x=-1,可得a0-a1+a2-a3+…+a100=(2+ )100.
与②中(*)式联立相减得
a1+a3+…+a99= .
专题探究四 二项式定理中的“赋值” 问题
④(a0+a2+…+a100)2-(a1+a3+…+a99)2.
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
原式=[(a0+a2+…+a100)+(a1+a3+…+a99)][(a0+a2+…+a100)-(a1+a3+…+a99)]
=(a0+a1+a2+…+a100)·(a0-a1+a2-a3+…+a98-a99+a100)
=[(2-)(2+)]100
=1100
=1.
专题探究四 二项式定理中的“赋值” 问题
⑤|a0|+|a1|+…+|a100|.
例4 (2)设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值.
因为Tr+1=(-1)r2100-r()rxr,
所以a2k-1<0(k∈N+).
所以|a0|+|a1|+|a2|+…+|a100|
=a0-a1+a2-a3+…+a100
=(2+ )100.
规律方法
赋值法的应用规律
与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和,主要方法是赋值法,通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
提醒:求各项系数的绝对值的和时,要先根据绝对值里面数的符号赋值求解.
跟踪训练
4.(1)已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn.若a1+a2+…+an-1=29-n,那么自然数n的值为( )
A.6 B.5 C.4 D.3
C
令x=1得2+22+23+…+2n=a0+a1+a2+…+an
即=a0+a1+a2+…+an,
即2n+1-2=a0+a1+a2+…+an
令x=0得a0=1+1+1+…+1=n,
∵an=1,∴a1+a2+…+an-1=2n+1-n-3,
∴2n+1-n-3=29-n,解得n=4.
跟踪训练
(2)若(1+x+x2)6=a0+a1x+a2x2+…+a12x12,则a2+a4+…+a12=________.
令x=0得,a0=1.
∴当x=1时,a0+a1+a2+…+a11+a12=36;①
当x=-1时,a0-a1+a2+…-a11+a12=1;②
①+②得2(a0+a2+a4+…+a12)=730,
∴a2+a4+a6+…+a12=364.
364
