人教版(2019)数学选择性必修三6.2.1-6.2.2排列与排列数课件(共36张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三6.2.1-6.2.2排列与排列数课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 507.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:35:23 | ||
图片预览








文档简介
(共36张PPT)
6.2.1-6.2.2 排列与排列数
高二
选择性必修三
1.了解排列、排列数的定义.
2.掌握排列数公式的推导方法.
3.能用排列数公式解决简单的排列问题.
本节目标
知识点一 排列的定义
1.在学校奖学金发放仪式上,校长和两位获得特等奖学金的男女同学合影留念.师生三人站成一排,校长站在中间.
问题1:男生在左边和女生在左边是相同的排法吗?
提示:不是.
问题2:有几种排法?
提示:2种,男—师—女,女—师—男.
提
出
问
题
新知探究
2.从甲、乙、丙三名同学中选出2人参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动.
问题1:让你安排这项活动需分几步?它们是什么?
提示:分两步:第1步,确定上午的同学;第2步,确定下午的同学.
问题2:有几种排法?
提示:上午有3种,下午有2种,因此共有3×2=6种排法.
问题3:甲乙和乙甲是相同的排法吗?
提示:不是.甲乙是甲上午、乙下午;乙甲是乙上午、甲下午.
提
出
问
题
导
入
新
知
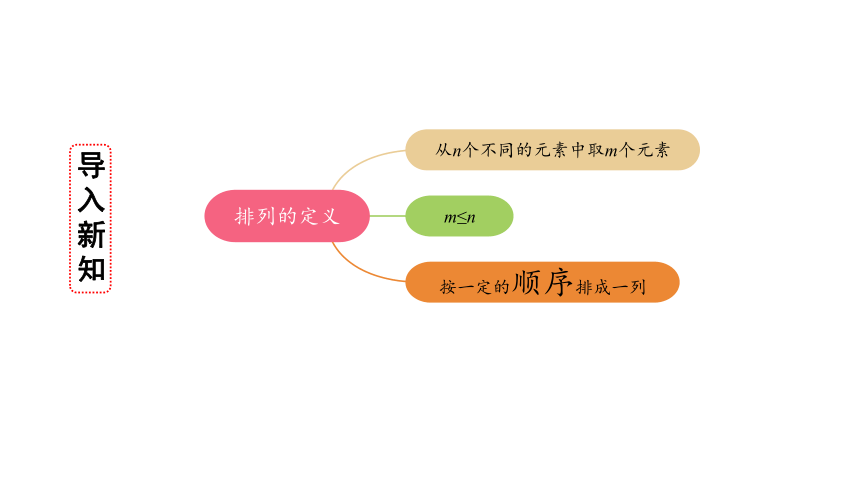
排列的定义
从n个不同的元素中取m个元素
m≤n
按一定的顺序排成一列
化解疑难
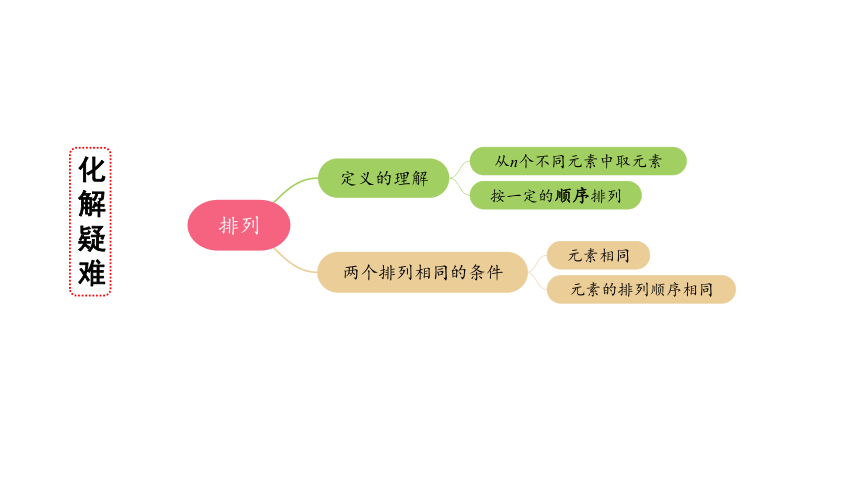
排列
定义的理解
两个排列相同的条件
从n个不同元素中取元素
按一定的顺序排列
元素相同
元素的排列顺序相同
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题1:从这4个数字中选出2个能构成多少个无重复数字的两位数?
提
出
问
题
无重复数字的两位数
第1步:确定个位
第2步:确定十位
4种选择
3种选择
4×3=12(个)
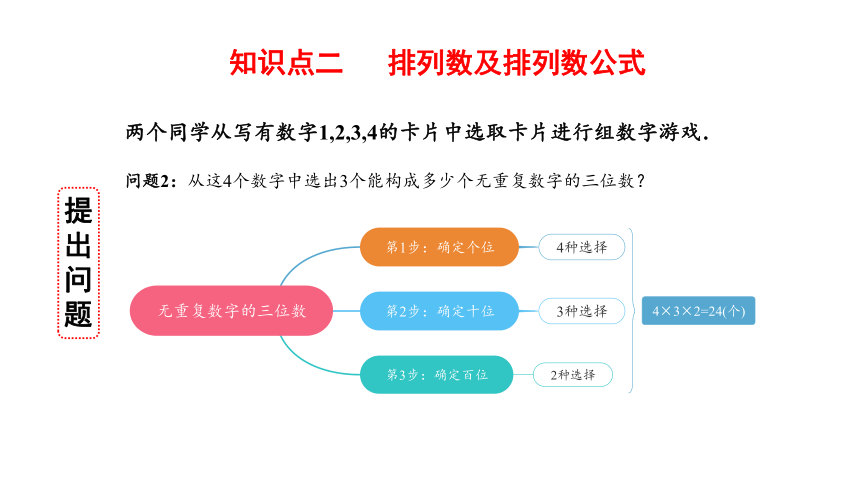
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题2:从这4个数字中选出3个能构成多少个无重复数字的三位数?
提
出
问
题
无重复数字的三位数
第1步:确定个位
第2步:确定十位
4种选择
3种选择
第3步:确定百位
2种选择
4×3×2=24(个)
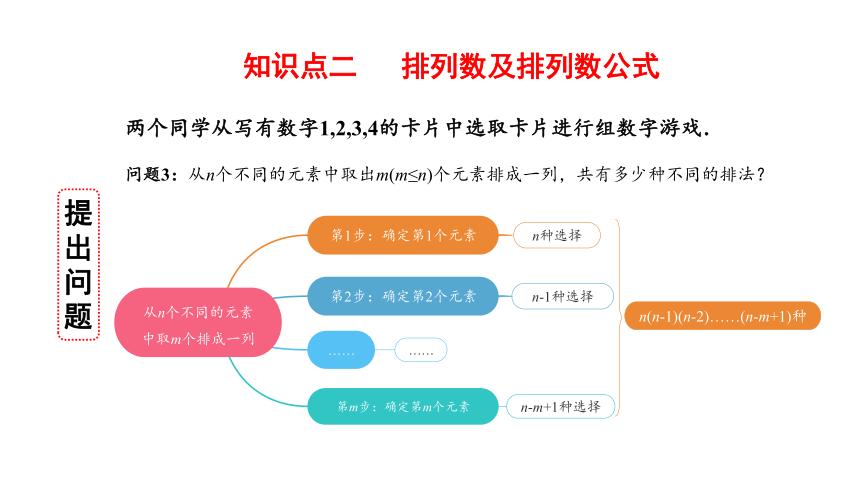
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题3:从n个不同的元素中取出m(m≤n)个元素排成一列,共有多少种不同的排法?
提
出
问
题
从n个不同的元素中取m个排成一列
第1步:确定第1个元素
第2步:确定第2个元素
n种选择
n-1种选择
……
……
第m步:确定第m个元素
n-m+1种选择
n(n-1)(n-2)……(n-m+1)种
排列数定义 及表示 从n个不同元素中取出m(m≤n)个元素的所有___________,叫做从n个不同元素中取出m个元素的排列数,用符号表示
排列数公式 =__________________________
阶乘式= (n,m∈N*,m≤n)
特殊情况 =_____,=____, 0!=1
排列的个数
n(n-1)(n-2)…(n-m+1)
n!
1
导
入
新
知
化解疑难
排列与排列数的区别
不是数
排列:完成一件事的方法
排列数:所有排列的个数
是数
符号中,m,n均为正整数,
且m≤n,是一个整体.
例1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其结果有多少种不同的可能?
(2)从1,2,3,4四个数字中,任选两个做除法有多少种不同的可能?
(3)会场有50个座位,要求选出3个座位有多少种方法?若选出3个座位安排3位客人入座,又有多少种方法?
题
型
一
排列的有关概念
典例精析
例1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其结果有多少种不同的可能?
不是
加法满足交换律,所以选出的两个元素做加法求结果时,与两个元素的位置无关。
例1 下列问题是排列问题吗?
(2)从1,2,3,4四个数字中,任选两个做除法有多少种不同的可能?
是
选出的数谁做除数,谁做被除数,结果不一样,此时与位置有关.
例1 下列问题是排列问题吗?
(3)会场有50个座位,要求选出3个座位有多少种方法?若选出3个座位安排3位客人入座,又有多少种方法?
1.不是
第1问:选出3个座位,与位置无关
2.是
第2问:安排3位客人入座,与位置有关
元素有序还是无序是判断是否是排列问题的关键
排列问题的
本质特征
取出的元素
无重复
取出的元素
必须按顺序排列
类题通法
判断下列问题是否为排列问题.
(1)北京、上海、天津三个民航站之间的直达航线的飞机票价格
(假设来回的票价相同);
不是
票价只有三种,不存在顺序问题,所以不是排列问题.
活学活用
判断下列问题是否为排列问题.
(2)选3个人分别担任班长、学习委员、生活委员;
是
每个人职务不同,事件结果就不同,如甲当班长或当学习委员是不同的,存在顺序问题,是排列问题.
判断下列问题是否为排列问题.
(3)某班40名学生在假期相互通信.
是
A给B写信与B给A写信是不同的,所以存在着顺序问题,是排列问题.
题
型
二
用列举法解决
排列问题
例2 写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
典例精析
例2 写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
1
2
3
4
12
13
14
2
1
3
4
21
23
24
3
1
2
4
31
32
34
4
1
2
3
41
42
43
3个
3个
3个
3个
3+3+3+3=12(个)
例2 写出下列问题的所有排列:
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
1
2
3
4
3
4
2
4
2
3
4
3
4
2
3
2
2
1
3
4
3
4
1
4
1
3
4
3
4
1
3
1
4
1
2
3
2
3
1
3
1
2
3
2
3
1
2
1
3
1
2
4
2
4
1
4
1
2
4
2
4
1
2
1
6个
6个
6个
6个
6+6+6+6=24(个)
将元素排序
以先安排哪个元素为分类标准进行分类
按此标准依次确定后边的元素
排列个数不多时使用
何时用?
怎么用?
为什么用?
可以做到不重不漏
类题通法
树形图
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
法一:卡选人
法二:人选卡
活学活用
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
B
A
C
D
D
D
C
A
A
C
法一:
设四张贺卡分别为A,B,C,D.
C
A
D
D
D
A
B
B
B
A
D
A
C
C
B
A
C
B
B
A
B
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
法二:
设A,B,C,D四人拿卡.
B
3种取法
3种取法
第一步:A取
第二步:被A取走的贺卡的主人拿
第三步:剩下的两人拿
各1种取法
3×3×1×1=9(种)
四人取卡
题
型
三 排列数公式的应用
例3 计算下列各题:
(2) ;
(3)若,求x.
(1);
典例精析
例3 计算下列各题:
(2) ;
(1) ;
(1) =6!=6×5×4×3×2×1=720.
(2)
例3 计算下列各题:
(3)若, 求x.
3x(x-1)(x-2)=2(x+1)x+6x(x-1)
3x2-17x+10=0
x=5 或 x= (舍去)
x≥3且x∈N+
最大的数是n,因式的个数是m
排列数的计算
先化简,再计算
连续正整数(因式)
的乘积可写成
类题通法
计算:
(1) ; (2) .
(1)
(2)原式=
活学活用
1.89×90×91×…×100可表示为( )
A. B. C. D.
=100×99×…×(100-12+1)=100×99×…×89.
C
随堂检测
2.A,B,C三名同学照相留念,呈“一”字形排队,所有排列的方法种数为( )
A.3 B.4 C.6 D.12
列举如下:A—B—C,A—C—B,B—A—C,
B—C—A,C—A—B,C—B—A.
C
3.满足不等式的n的最小值为________.
由排列数公式得,即(n-5)(n-6)>12,
解得n>9或n<2.
又n≥7,所以n>9,又n∈N*,
所以n的最小值为10.
10
4.一次演出,因临时有变化,拟在已安排好的4个节目的基础上再添加2个小品节目,且2个小品节目不相邻,则不同的添加方法共有________种.
从原来4个节目形成的5个空中选2个空排列,共有=20种添加方法.
20
5.写出从a,b,c,d这4个字母中,每次取出2个字母的所有排列.
a
b
c
d
b
a
c
d
c
a
b
d
d
a
b
c
因此,共计有12个不同的排列,它们是ab,ac,ad,ba,bc,bd,ca,cb,cd,da,db,dc.
6.2.1-6.2.2 排列与排列数
高二
选择性必修三
1.了解排列、排列数的定义.
2.掌握排列数公式的推导方法.
3.能用排列数公式解决简单的排列问题.
本节目标
知识点一 排列的定义
1.在学校奖学金发放仪式上,校长和两位获得特等奖学金的男女同学合影留念.师生三人站成一排,校长站在中间.
问题1:男生在左边和女生在左边是相同的排法吗?
提示:不是.
问题2:有几种排法?
提示:2种,男—师—女,女—师—男.
提
出
问
题
新知探究
2.从甲、乙、丙三名同学中选出2人参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动.
问题1:让你安排这项活动需分几步?它们是什么?
提示:分两步:第1步,确定上午的同学;第2步,确定下午的同学.
问题2:有几种排法?
提示:上午有3种,下午有2种,因此共有3×2=6种排法.
问题3:甲乙和乙甲是相同的排法吗?
提示:不是.甲乙是甲上午、乙下午;乙甲是乙上午、甲下午.
提
出
问
题
导
入
新
知
排列的定义
从n个不同的元素中取m个元素
m≤n
按一定的顺序排成一列
化解疑难
排列
定义的理解
两个排列相同的条件
从n个不同元素中取元素
按一定的顺序排列
元素相同
元素的排列顺序相同
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题1:从这4个数字中选出2个能构成多少个无重复数字的两位数?
提
出
问
题
无重复数字的两位数
第1步:确定个位
第2步:确定十位
4种选择
3种选择
4×3=12(个)
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题2:从这4个数字中选出3个能构成多少个无重复数字的三位数?
提
出
问
题
无重复数字的三位数
第1步:确定个位
第2步:确定十位
4种选择
3种选择
第3步:确定百位
2种选择
4×3×2=24(个)
知识点二 排列数及排列数公式
两个同学从写有数字1,2,3,4的卡片中选取卡片进行组数字游戏.
问题3:从n个不同的元素中取出m(m≤n)个元素排成一列,共有多少种不同的排法?
提
出
问
题
从n个不同的元素中取m个排成一列
第1步:确定第1个元素
第2步:确定第2个元素
n种选择
n-1种选择
……
……
第m步:确定第m个元素
n-m+1种选择
n(n-1)(n-2)……(n-m+1)种
排列数定义 及表示 从n个不同元素中取出m(m≤n)个元素的所有___________,叫做从n个不同元素中取出m个元素的排列数,用符号表示
排列数公式 =__________________________
阶乘式= (n,m∈N*,m≤n)
特殊情况 =_____,=____, 0!=1
排列的个数
n(n-1)(n-2)…(n-m+1)
n!
1
导
入
新
知
化解疑难
排列与排列数的区别
不是数
排列:完成一件事的方法
排列数:所有排列的个数
是数
符号中,m,n均为正整数,
且m≤n,是一个整体.
例1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其结果有多少种不同的可能?
(2)从1,2,3,4四个数字中,任选两个做除法有多少种不同的可能?
(3)会场有50个座位,要求选出3个座位有多少种方法?若选出3个座位安排3位客人入座,又有多少种方法?
题
型
一
排列的有关概念
典例精析
例1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其结果有多少种不同的可能?
不是
加法满足交换律,所以选出的两个元素做加法求结果时,与两个元素的位置无关。
例1 下列问题是排列问题吗?
(2)从1,2,3,4四个数字中,任选两个做除法有多少种不同的可能?
是
选出的数谁做除数,谁做被除数,结果不一样,此时与位置有关.
例1 下列问题是排列问题吗?
(3)会场有50个座位,要求选出3个座位有多少种方法?若选出3个座位安排3位客人入座,又有多少种方法?
1.不是
第1问:选出3个座位,与位置无关
2.是
第2问:安排3位客人入座,与位置有关
元素有序还是无序是判断是否是排列问题的关键
排列问题的
本质特征
取出的元素
无重复
取出的元素
必须按顺序排列
类题通法
判断下列问题是否为排列问题.
(1)北京、上海、天津三个民航站之间的直达航线的飞机票价格
(假设来回的票价相同);
不是
票价只有三种,不存在顺序问题,所以不是排列问题.
活学活用
判断下列问题是否为排列问题.
(2)选3个人分别担任班长、学习委员、生活委员;
是
每个人职务不同,事件结果就不同,如甲当班长或当学习委员是不同的,存在顺序问题,是排列问题.
判断下列问题是否为排列问题.
(3)某班40名学生在假期相互通信.
是
A给B写信与B给A写信是不同的,所以存在着顺序问题,是排列问题.
题
型
二
用列举法解决
排列问题
例2 写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
典例精析
例2 写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
1
2
3
4
12
13
14
2
1
3
4
21
23
24
3
1
2
4
31
32
34
4
1
2
3
41
42
43
3个
3个
3个
3个
3+3+3+3=12(个)
例2 写出下列问题的所有排列:
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
1
2
3
4
3
4
2
4
2
3
4
3
4
2
3
2
2
1
3
4
3
4
1
4
1
3
4
3
4
1
3
1
4
1
2
3
2
3
1
3
1
2
3
2
3
1
2
1
3
1
2
4
2
4
1
4
1
2
4
2
4
1
2
1
6个
6个
6个
6个
6+6+6+6=24(个)
将元素排序
以先安排哪个元素为分类标准进行分类
按此标准依次确定后边的元素
排列个数不多时使用
何时用?
怎么用?
为什么用?
可以做到不重不漏
类题通法
树形图
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
法一:卡选人
法二:人选卡
活学活用
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
B
A
C
D
D
D
C
A
A
C
法一:
设四张贺卡分别为A,B,C,D.
C
A
D
D
D
A
B
B
B
A
D
A
C
C
B
A
C
B
B
A
B
同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
法二:
设A,B,C,D四人拿卡.
B
3种取法
3种取法
第一步:A取
第二步:被A取走的贺卡的主人拿
第三步:剩下的两人拿
各1种取法
3×3×1×1=9(种)
四人取卡
题
型
三 排列数公式的应用
例3 计算下列各题:
(2) ;
(3)若,求x.
(1);
典例精析
例3 计算下列各题:
(2) ;
(1) ;
(1) =6!=6×5×4×3×2×1=720.
(2)
例3 计算下列各题:
(3)若, 求x.
3x(x-1)(x-2)=2(x+1)x+6x(x-1)
3x2-17x+10=0
x=5 或 x= (舍去)
x≥3且x∈N+
最大的数是n,因式的个数是m
排列数的计算
先化简,再计算
连续正整数(因式)
的乘积可写成
类题通法
计算:
(1) ; (2) .
(1)
(2)原式=
活学活用
1.89×90×91×…×100可表示为( )
A. B. C. D.
=100×99×…×(100-12+1)=100×99×…×89.
C
随堂检测
2.A,B,C三名同学照相留念,呈“一”字形排队,所有排列的方法种数为( )
A.3 B.4 C.6 D.12
列举如下:A—B—C,A—C—B,B—A—C,
B—C—A,C—A—B,C—B—A.
C
3.满足不等式的n的最小值为________.
由排列数公式得,即(n-5)(n-6)>12,
解得n>9或n<2.
又n≥7,所以n>9,又n∈N*,
所以n的最小值为10.
10
4.一次演出,因临时有变化,拟在已安排好的4个节目的基础上再添加2个小品节目,且2个小品节目不相邻,则不同的添加方法共有________种.
从原来4个节目形成的5个空中选2个空排列,共有=20种添加方法.
20
5.写出从a,b,c,d这4个字母中,每次取出2个字母的所有排列.
a
b
c
d
b
a
c
d
c
a
b
d
d
a
b
c
因此,共计有12个不同的排列,它们是ab,ac,ad,ba,bc,bd,ca,cb,cd,da,db,dc.
