人教版(2019)数学选择性必修三6.2.2排列的综合应用课件(共28张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三6.2.2排列的综合应用课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 502.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
6.2.2 排列的综合应用
高二
选择性必修三
1.进一步理解排列的意义,并能用排列数公式进行运算.
2.能用所学的排列知识解决简单的实际问题,掌握常用方法:直接法(如特殊元素处理法、特殊位置处理法、捆绑法、插空法等)、间接法.
3.通过实例分析过程,体验知识的形成和发展,总结规律,培养兴趣.
本节目标
考点回顾
两个计数原理有何区别?
排列与排列数有何不同?
知识点拨
题
型
一
无限制条件的排列问题
例1 有5个不同的科研小课题,从中选3个由高二(4)班的3个学习兴趣小组进行研究,每组一个课题,共有多少种不同的安排方法?
典例精析
例1 有5个不同的科研小课题,从中选3个由高二(4)班的3个学习兴趣小组进行研究,每组一个课题,共有多少种不同的安排方法?
有=5×4×3=60种不同的安排方法.
5个中选3个
分给3个小组
难易度:相对简单
策略:分清元素和位置即可
没有限制的
排列问题
对元素和位置没有特别的限制
类题通法
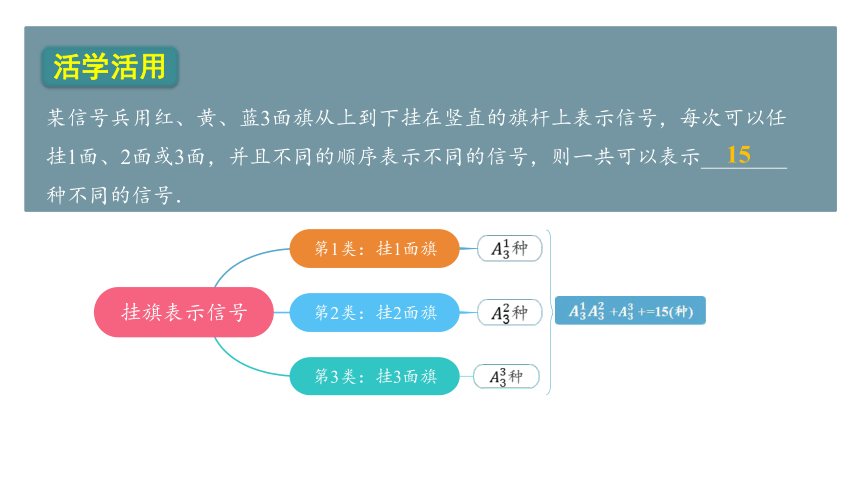
某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,则一共可以表示________种不同的信号.
挂旗表示信号
第1类:挂1面旗
第2类:挂2面旗
种
种
第3类:挂3面旗
种
+ + =15(种)
活学活用
15
题
型
二
在
与不在
的问题
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(1)甲不站中间,也不站两端;
(2)甲、乙两人必须站两端.
典例精析
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(1)甲不站中间,也不站两端;
甲不站中间
也不站两端
第1步:排两端及
中间的位置
第2步:排剩余的
4个位置
种
种
× =2880(种)
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(2)甲、乙两人必须站两端.
甲、乙两人
必须站两端
第1步:排甲乙
第2步:其余5人全排列
种
种
×=240(种)
从元素入手
从位置入手
先排特殊元素
再排其它元素
先排特殊位置
再排其它位置
“在”与“不在”有限制条件的排列问题
谁特殊,谁优先
类题通法
乒乓球队的10名队员中有3名主力队员,派5名参加比赛,3名主力队员安排在第一、三、五位置,其余7名队员中选2名安排在第二、四位置上,那么不同的出场安排有________种.
出场安排有多少种?
第1步:安排3名主力队员
第2步:安排另两名队员
种
种
×=252(种)
252
活学活用
题
型
三
相邻与不相邻问题
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例精析
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
男生站在一起:是男生的全排列,有种排法;
女生站在一起:是女生的全排列,有种排法;
全体男生、女生各视为一个元素:有种排法.
由分步计数原理知,共有· · =288种排队方法.
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(2)全体站成一排,男生必须站在一起;
①三个男生全排列:有种方法,
②把所有男生视为一个元素,与4名女生组成5个元素全排列:有种排法.
故有· =720种排队方法.
捆绑法
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(3)全体站成一排,男生不能站在一起;
先安排女生,共有种排法;
男生在4个女生隔成的5个空中安排,共有种排法,故共有· =1440种排法.
插空法
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(4)全体站成一排,男、女各不相邻.
排好男生后让女生插空,共有· =144种排法.
插空法
捆绑法
插空法
排列问题的
解题方法
相邻问题
不相邻问题
类题通法
7人站成一排.求:
(1)甲、乙两人相邻的排法有多少种?
捆绑法
将甲、乙两人“捆绑”为一个元素,与其余5人全排列,共有种排法.
甲、乙两人可交换位置,有种排法.
故共有·=1440种排法.
活学活用
7人站成一排.求:
(2)甲、乙两人不相邻的排法有多少种?
插空法
将其余5人排列,有种排法,
5人之间及两端共有6个位置,任选2个排甲、乙两人,有种排法.
故共有·=3600种排法.
7人站成一排.求:
(3)甲、乙、丙三人必相邻的排法有多少种?
捆绑法
将甲、乙、丙三人捆绑在一起与其余4人全排列,有种排法,
甲、乙、丙三人有种排法,共有·=720种排法.
7人站成一排.求:
(4)甲、乙、丙三人两两不相邻的排法有多少种?
插空法
将其余4人排好,有种排法.
将甲、乙、丙插入5个空中,有种排法.
故共有·=1440种排法.
1.6名学生排成两排,每排3人,则不同的排法种数为( )
A.36 B.120 C.720 D.240
6人排两排,没有特殊要求的元素,故排法种数为=720.
C
随堂检测
2.要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
A.1440种 B.960种 C.720种 D.480种
从5名志愿者中选2人排在两端有种排法,
2位老人的排法有种,
其余3人和老人排有种排法,
共有 =960种不同的排法.
B
3.若把英语单词“good”的字母顺序写错了,则可能出现的错误共有________种.
因为good有两个相同字母,
所以可能出现-1=11种错误.
11
4.从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有________种(用数字作答).
解题策略
第1步:选文娱委员
第2步:选学习委员和
体育委员
3种选法
种选法
3× =36(种)
36
5.喜羊羊家族的四位成员与灰太狼,红太狼进行谈判,通过谈判他们握手言和,准备一起照合影像(排成一排).
(1)要求喜羊羊家族的四位成员必须相邻,有多少种排法?
捆绑法
把喜羊羊家族的四位成员看成一个元素,排法为.
又因为四位成员交换顺序产生不同排列,所以共有·=144种排法.
5.喜羊羊家族的四位成员与灰太狼,红太狼进行谈判,通过谈判他们握手言和,准备一起照合影像(排成一排).
(2)要求灰太狼、红太狼不相邻,有多少种排法?
插空法
解题策略
第1步:排喜羊羊家族
的4位成员
第2步:灰太狼、红太狼插空
种选法
种选法
×=480(种)
6.2.2 排列的综合应用
高二
选择性必修三
1.进一步理解排列的意义,并能用排列数公式进行运算.
2.能用所学的排列知识解决简单的实际问题,掌握常用方法:直接法(如特殊元素处理法、特殊位置处理法、捆绑法、插空法等)、间接法.
3.通过实例分析过程,体验知识的形成和发展,总结规律,培养兴趣.
本节目标
考点回顾
两个计数原理有何区别?
排列与排列数有何不同?
知识点拨
题
型
一
无限制条件的排列问题
例1 有5个不同的科研小课题,从中选3个由高二(4)班的3个学习兴趣小组进行研究,每组一个课题,共有多少种不同的安排方法?
典例精析
例1 有5个不同的科研小课题,从中选3个由高二(4)班的3个学习兴趣小组进行研究,每组一个课题,共有多少种不同的安排方法?
有=5×4×3=60种不同的安排方法.
5个中选3个
分给3个小组
难易度:相对简单
策略:分清元素和位置即可
没有限制的
排列问题
对元素和位置没有特别的限制
类题通法
某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,则一共可以表示________种不同的信号.
挂旗表示信号
第1类:挂1面旗
第2类:挂2面旗
种
种
第3类:挂3面旗
种
+ + =15(种)
活学活用
15
题
型
二
在
与不在
的问题
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(1)甲不站中间,也不站两端;
(2)甲、乙两人必须站两端.
典例精析
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(1)甲不站中间,也不站两端;
甲不站中间
也不站两端
第1步:排两端及
中间的位置
第2步:排剩余的
4个位置
种
种
× =2880(种)
例2 3名男生、4名女生,按照不同的要求站成一排,求不同的排队方案有多少种.
(2)甲、乙两人必须站两端.
甲、乙两人
必须站两端
第1步:排甲乙
第2步:其余5人全排列
种
种
×=240(种)
从元素入手
从位置入手
先排特殊元素
再排其它元素
先排特殊位置
再排其它位置
“在”与“不在”有限制条件的排列问题
谁特殊,谁优先
类题通法
乒乓球队的10名队员中有3名主力队员,派5名参加比赛,3名主力队员安排在第一、三、五位置,其余7名队员中选2名安排在第二、四位置上,那么不同的出场安排有________种.
出场安排有多少种?
第1步:安排3名主力队员
第2步:安排另两名队员
种
种
×=252(种)
252
活学活用
题
型
三
相邻与不相邻问题
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例精析
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
男生站在一起:是男生的全排列,有种排法;
女生站在一起:是女生的全排列,有种排法;
全体男生、女生各视为一个元素:有种排法.
由分步计数原理知,共有· · =288种排队方法.
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(2)全体站成一排,男生必须站在一起;
①三个男生全排列:有种方法,
②把所有男生视为一个元素,与4名女生组成5个元素全排列:有种排法.
故有· =720种排队方法.
捆绑法
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(3)全体站成一排,男生不能站在一起;
先安排女生,共有种排法;
男生在4个女生隔成的5个空中安排,共有种排法,故共有· =1440种排法.
插空法
例3 3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(4)全体站成一排,男、女各不相邻.
排好男生后让女生插空,共有· =144种排法.
插空法
捆绑法
插空法
排列问题的
解题方法
相邻问题
不相邻问题
类题通法
7人站成一排.求:
(1)甲、乙两人相邻的排法有多少种?
捆绑法
将甲、乙两人“捆绑”为一个元素,与其余5人全排列,共有种排法.
甲、乙两人可交换位置,有种排法.
故共有·=1440种排法.
活学活用
7人站成一排.求:
(2)甲、乙两人不相邻的排法有多少种?
插空法
将其余5人排列,有种排法,
5人之间及两端共有6个位置,任选2个排甲、乙两人,有种排法.
故共有·=3600种排法.
7人站成一排.求:
(3)甲、乙、丙三人必相邻的排法有多少种?
捆绑法
将甲、乙、丙三人捆绑在一起与其余4人全排列,有种排法,
甲、乙、丙三人有种排法,共有·=720种排法.
7人站成一排.求:
(4)甲、乙、丙三人两两不相邻的排法有多少种?
插空法
将其余4人排好,有种排法.
将甲、乙、丙插入5个空中,有种排法.
故共有·=1440种排法.
1.6名学生排成两排,每排3人,则不同的排法种数为( )
A.36 B.120 C.720 D.240
6人排两排,没有特殊要求的元素,故排法种数为=720.
C
随堂检测
2.要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
A.1440种 B.960种 C.720种 D.480种
从5名志愿者中选2人排在两端有种排法,
2位老人的排法有种,
其余3人和老人排有种排法,
共有 =960种不同的排法.
B
3.若把英语单词“good”的字母顺序写错了,则可能出现的错误共有________种.
因为good有两个相同字母,
所以可能出现-1=11种错误.
11
4.从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有________种(用数字作答).
解题策略
第1步:选文娱委员
第2步:选学习委员和
体育委员
3种选法
种选法
3× =36(种)
36
5.喜羊羊家族的四位成员与灰太狼,红太狼进行谈判,通过谈判他们握手言和,准备一起照合影像(排成一排).
(1)要求喜羊羊家族的四位成员必须相邻,有多少种排法?
捆绑法
把喜羊羊家族的四位成员看成一个元素,排法为.
又因为四位成员交换顺序产生不同排列,所以共有·=144种排法.
5.喜羊羊家族的四位成员与灰太狼,红太狼进行谈判,通过谈判他们握手言和,准备一起照合影像(排成一排).
(2)要求灰太狼、红太狼不相邻,有多少种排法?
插空法
解题策略
第1步:排喜羊羊家族
的4位成员
第2步:灰太狼、红太狼插空
种选法
种选法
×=480(种)
