人教版(2019)数学选择性必修三6.2.3-6.2.4组合与组合数课件(共37张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三6.2.3-6.2.4组合与组合数课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 639.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:36:17 | ||
图片预览








文档简介
(共37张PPT)
6.2.3-6.2.4 组合与组合数
高二
选择性必修三
1.理解组合的定义,正确认识组合与排列的区别与联系.
2.理解排列数与组合数的联系,掌握组合数公式,能用组合数公式进行计算.
3.会解决一些简单的组合问题.
本节目标
知识点一 组合与组合数
提
出
问
题
从1,3,5,7中任取两个数相除或相乘.
问题1:所得商和积的个数相同吗?
提示:不相同.
问题2:它们是排列吗?
提示:从1,3,5,7中任取两个数相除是排列,而相乘不是排列.
两数相乘,交换位置,积不变,但商变.
新知探究
导
入
新
知
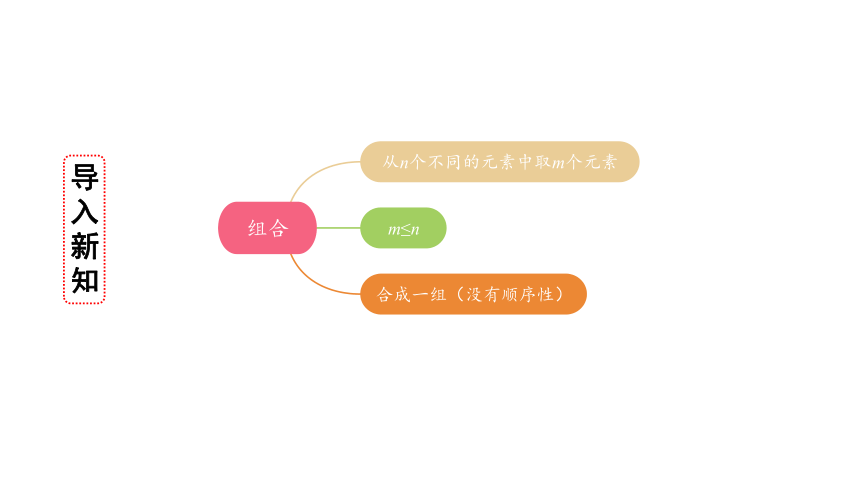
组合
从n个不同的元素中取m个元素
m≤n
合成一组(没有顺序性)
导
入
新
知
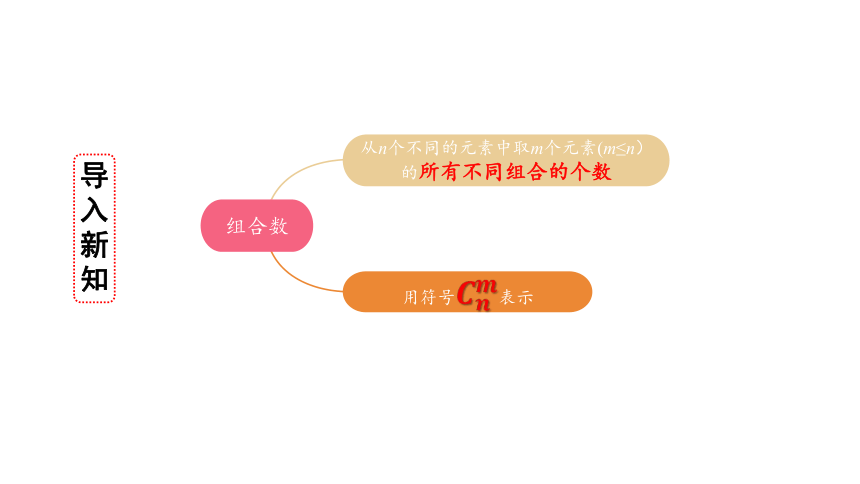
组合数
从n个不同的元素中取m个元素(m≤n)的所有不同组合的个数
用符号表示
化解疑难
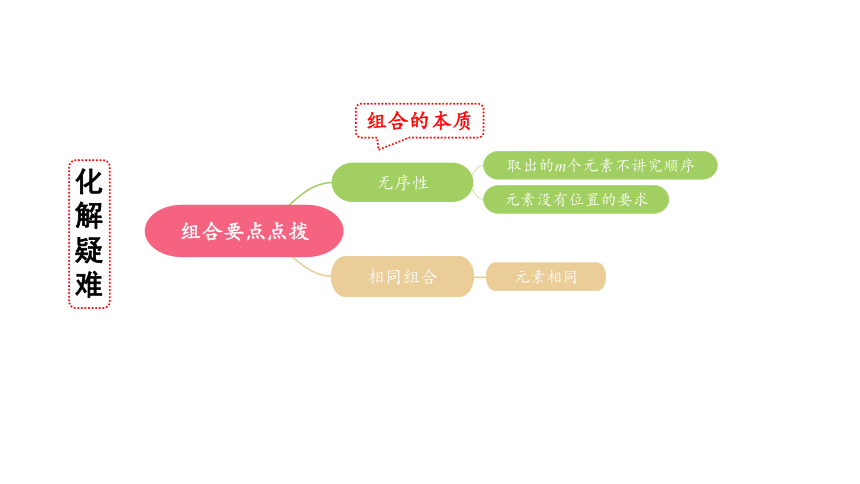
无序性
相同组合
取出的m个元素不讲究顺序
元素没有位置的要求
元素相同
组合要点点拨
组合的本质
知识点二 组合数公式
提
出
问
题
从1,3,5,7中任取两个数相除.
问题1:可以得到多少个不同的商?
提示:=4×3=12个不同的商.
问题2:如何用分步法求商的个数?
提示:第1步,从这四个数中任取两个数,有种方法;
第2步,将每个组合中的两个数排列,有种排法.
由分步乘法计数原理,可得商的个数为.
问题3:由问题1,2你能得出计算的公式吗?
提示:能.因为= ,所以==6.
问题4:你能把问题3的结论推广到一般吗?
提示:
知识点二 组合数公式
提
出
问
题
从1,3,5,7中任取两个数相除.
第一步:从n个元素中取m个元素
第二步:对m个元素全排列
种取法
种排法
= ·
=.
导
入
新
知
组合数公式 乘积形式
阶乘形式
性质 ①;②
备注 ①n,m∈N*,m≤n;②规定,
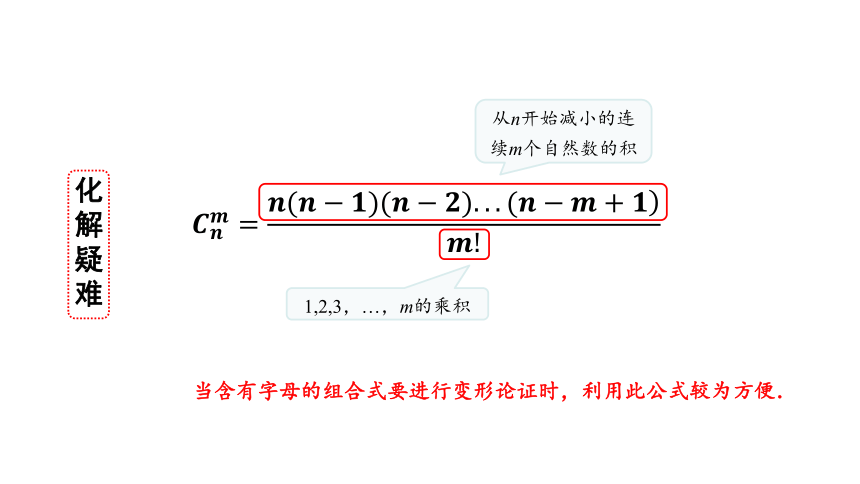
化解疑难
从n开始减小的连续m个自然数的积
1,2,3,…,m的乘积
当含有字母的组合式要进行变形论证时,利用此公式较为方便.
题
型
一
组合的有关概念
例1 判断下列各事件是排列问题,还是组合问题.
(1)10个人相互各写一封信,共写多少封信?
(2)10个人相互通一次电话,共通了多少次电话?
(3)从10个人中选3个代表去开会,有多少种选法?
(4)从10个人里选出3个不同学科的代表,有多少种选法?
典例精析
例1 判断下列各事件是排列问题,还是组合问题.
(1)10个人相互各写一封信,共写多少封信?
排列
因为发信人与收信人是有区别的.
例1 判断下列各事件是排列问题,还是组合问题.
(2)10个人相互通一次电话,共通了多少次电话?
组合
甲与乙通了一次电话,也就是乙与甲通了一次电话,没有顺序的区别.
例1 判断下列各事件是排列问题,还是组合问题.
(3)从10个人中选3个代表去开会,有多少种选法?
组合
3个代表之间没有顺序的区别.
例1 判断下列各事件是排列问题,还是组合问题.
(4)从10个人里选出3个不同学科的代表,有多少种选法?
排列
3个人中,担任哪一科的代表是有顺序区别的.
排列与组合问题区分方法
先确定事件
然后看是否与顺序
有关
有关是排列
无关是组合
类题通法
从5个不同的元素a,b,c,d,e中取出2个,写出所有不同的组合.
由此可得所有的组合为
ab,ac,ad,ae,bc,bd,be,cd,ce,de.
活学活用
题
型
二
与组合数有关的计算
(1)计算:;
(2)已知,求.
典例精析
(1)计算:
原式=
=
(2)已知 ,
求.
即
即m2-23m+42=0,解得m=2或21.
而0≤m≤5,∴m=2.
∴.
组合数
计算技巧
m较大时,利用性质①
计算组合数之和时,
常用性质②
类题通法
2. (1)计算:;
原式=
56+4 950
=5006
活学活用
2. (2)求等式中的n值.
化简原方程:,
解方程:n=9或n=-6(不合题意,舍去)
化简整理:n2-3n-54=0
n=9
题
型
三
简单的组合问题
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
(2)甲、乙、丙三人必需参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
典例精析
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
组合
共有=792种不同的选法.
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(2)甲、乙、丙三人必需参加;
组合
共有=36种不同的选法.
只需要从另外9人中选2人
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(3)甲、乙、丙三人不能参加;
组合
共有=126种不同的选法.
只需要从另外9人中选5人
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(4)甲、乙、丙三人只能有1人参加.
分两步
第1步:甲乙丙中选1人
第2步:另外9人中选4人
甲乙丙只能1人参加
种选法
种选法
× =378(种)
弄清事件本身
思考选出的元素是否与顺序有关
结合计数原理,运用组合公式求结果
解答简单组合问题的技巧
类题通法
3. 现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名教师去参加会议,有多少种不同的选法?
有45种不同的选法
活学活用
3. 现有10名教师,其中男教师6名,女教师4名.
(2)选出2名男教师或2名女教师去外地学习的选法有多少种?
选2名男教师或2名女教师
第1类:选2名男教师
第2类:选2名女教师
种选法
种选法
(种)
分类
3. 现有10名教师,其中男教师6名,女教师4名.
(3)现要从中选出男、女教师各2名去参加会议,有多少种不同的选法?
选男、女教师各2名
第1步:选2名男教师
第2步:选2名女教师
种选法
种选法
(种)
分步
1.方程的解为( )
A.4或9 B.4 C.9 D.其他
A
当x=3x-8时,解得x=4;
当28-x=3x-8时,解得x=9.
随堂检测
2.某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )
A.14 B.24 C.28 D.48
从6人中任选4人的选法为:=15
其中没有女生的选法有1种
故至少有1名女生的选法种数为15-1=14
A
排除法
3.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有________种.
父母应为A或B或O,共有·=9种情况
父母血型一定不是AB
9
4.10个人分成甲、乙两组,甲组4人、乙组6人,则不同的分组种数为________(用数字作答).
故共有不同的分组种数为=210.
210
先给甲组选4人,余下的6人为乙组
方法
5.某科技小组有女同学2名、男同学x名,现从中选出3人去参观展览.若恰有1名女生入选时的不同选法有20种,求该科技小组中男生的人数.
女同学选1人,男同学选2人
x=5
6.2.3-6.2.4 组合与组合数
高二
选择性必修三
1.理解组合的定义,正确认识组合与排列的区别与联系.
2.理解排列数与组合数的联系,掌握组合数公式,能用组合数公式进行计算.
3.会解决一些简单的组合问题.
本节目标
知识点一 组合与组合数
提
出
问
题
从1,3,5,7中任取两个数相除或相乘.
问题1:所得商和积的个数相同吗?
提示:不相同.
问题2:它们是排列吗?
提示:从1,3,5,7中任取两个数相除是排列,而相乘不是排列.
两数相乘,交换位置,积不变,但商变.
新知探究
导
入
新
知
组合
从n个不同的元素中取m个元素
m≤n
合成一组(没有顺序性)
导
入
新
知
组合数
从n个不同的元素中取m个元素(m≤n)的所有不同组合的个数
用符号表示
化解疑难
无序性
相同组合
取出的m个元素不讲究顺序
元素没有位置的要求
元素相同
组合要点点拨
组合的本质
知识点二 组合数公式
提
出
问
题
从1,3,5,7中任取两个数相除.
问题1:可以得到多少个不同的商?
提示:=4×3=12个不同的商.
问题2:如何用分步法求商的个数?
提示:第1步,从这四个数中任取两个数,有种方法;
第2步,将每个组合中的两个数排列,有种排法.
由分步乘法计数原理,可得商的个数为.
问题3:由问题1,2你能得出计算的公式吗?
提示:能.因为= ,所以==6.
问题4:你能把问题3的结论推广到一般吗?
提示:
知识点二 组合数公式
提
出
问
题
从1,3,5,7中任取两个数相除.
第一步:从n个元素中取m个元素
第二步:对m个元素全排列
种取法
种排法
= ·
=.
导
入
新
知
组合数公式 乘积形式
阶乘形式
性质 ①;②
备注 ①n,m∈N*,m≤n;②规定,
化解疑难
从n开始减小的连续m个自然数的积
1,2,3,…,m的乘积
当含有字母的组合式要进行变形论证时,利用此公式较为方便.
题
型
一
组合的有关概念
例1 判断下列各事件是排列问题,还是组合问题.
(1)10个人相互各写一封信,共写多少封信?
(2)10个人相互通一次电话,共通了多少次电话?
(3)从10个人中选3个代表去开会,有多少种选法?
(4)从10个人里选出3个不同学科的代表,有多少种选法?
典例精析
例1 判断下列各事件是排列问题,还是组合问题.
(1)10个人相互各写一封信,共写多少封信?
排列
因为发信人与收信人是有区别的.
例1 判断下列各事件是排列问题,还是组合问题.
(2)10个人相互通一次电话,共通了多少次电话?
组合
甲与乙通了一次电话,也就是乙与甲通了一次电话,没有顺序的区别.
例1 判断下列各事件是排列问题,还是组合问题.
(3)从10个人中选3个代表去开会,有多少种选法?
组合
3个代表之间没有顺序的区别.
例1 判断下列各事件是排列问题,还是组合问题.
(4)从10个人里选出3个不同学科的代表,有多少种选法?
排列
3个人中,担任哪一科的代表是有顺序区别的.
排列与组合问题区分方法
先确定事件
然后看是否与顺序
有关
有关是排列
无关是组合
类题通法
从5个不同的元素a,b,c,d,e中取出2个,写出所有不同的组合.
由此可得所有的组合为
ab,ac,ad,ae,bc,bd,be,cd,ce,de.
活学活用
题
型
二
与组合数有关的计算
(1)计算:;
(2)已知,求.
典例精析
(1)计算:
原式=
=
(2)已知 ,
求.
即
即m2-23m+42=0,解得m=2或21.
而0≤m≤5,∴m=2.
∴.
组合数
计算技巧
m较大时,利用性质①
计算组合数之和时,
常用性质②
类题通法
2. (1)计算:;
原式=
56+4 950
=5006
活学活用
2. (2)求等式中的n值.
化简原方程:,
解方程:n=9或n=-6(不合题意,舍去)
化简整理:n2-3n-54=0
n=9
题
型
三
简单的组合问题
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
(2)甲、乙、丙三人必需参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
典例精析
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
组合
共有=792种不同的选法.
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(2)甲、乙、丙三人必需参加;
组合
共有=36种不同的选法.
只需要从另外9人中选2人
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(3)甲、乙、丙三人不能参加;
组合
共有=126种不同的选法.
只需要从另外9人中选5人
例3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(4)甲、乙、丙三人只能有1人参加.
分两步
第1步:甲乙丙中选1人
第2步:另外9人中选4人
甲乙丙只能1人参加
种选法
种选法
× =378(种)
弄清事件本身
思考选出的元素是否与顺序有关
结合计数原理,运用组合公式求结果
解答简单组合问题的技巧
类题通法
3. 现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名教师去参加会议,有多少种不同的选法?
有45种不同的选法
活学活用
3. 现有10名教师,其中男教师6名,女教师4名.
(2)选出2名男教师或2名女教师去外地学习的选法有多少种?
选2名男教师或2名女教师
第1类:选2名男教师
第2类:选2名女教师
种选法
种选法
(种)
分类
3. 现有10名教师,其中男教师6名,女教师4名.
(3)现要从中选出男、女教师各2名去参加会议,有多少种不同的选法?
选男、女教师各2名
第1步:选2名男教师
第2步:选2名女教师
种选法
种选法
(种)
分步
1.方程的解为( )
A.4或9 B.4 C.9 D.其他
A
当x=3x-8时,解得x=4;
当28-x=3x-8时,解得x=9.
随堂检测
2.某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )
A.14 B.24 C.28 D.48
从6人中任选4人的选法为:=15
其中没有女生的选法有1种
故至少有1名女生的选法种数为15-1=14
A
排除法
3.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有________种.
父母应为A或B或O,共有·=9种情况
父母血型一定不是AB
9
4.10个人分成甲、乙两组,甲组4人、乙组6人,则不同的分组种数为________(用数字作答).
故共有不同的分组种数为=210.
210
先给甲组选4人,余下的6人为乙组
方法
5.某科技小组有女同学2名、男同学x名,现从中选出3人去参观展览.若恰有1名女生入选时的不同选法有20种,求该科技小组中男生的人数.
女同学选1人,男同学选2人
x=5
