人教版(2019)数学选择性必修三6.2.4组合的应用课件(共26张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三6.2.4组合的应用课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 451.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:52:19 | ||
图片预览



文档简介
(共26张PPT)
6.2.4 组合的应用
高二
选择性必修三
1.进一步理解组合的定义,熟练掌握组合数公式的应用.
2.能解决含有限制条件的组合问题,掌握常见的类型及解决策略.
3.体会简单的排列组合综合问题.
本节目标
考点回顾
排列与组合的
不同点是什么?
利用组合数的性质
应注意什么?
思考总结
题
型
一
组合问题的简单应用
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(1)如果小组中至少有3名女生,可有多少种不同的选法?
(2)如果小组中至少有5名男生,可有多少种不同的选法?
(3)如果小组中至多有3名女生,可有多少种不同的选法?
典例精析
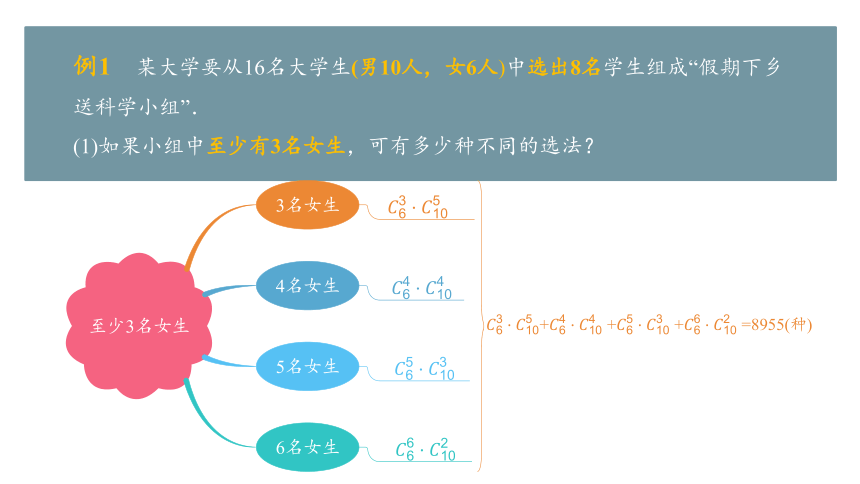
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(1)如果小组中至少有3名女生,可有多少种不同的选法?
至少3名女生
3名女生
4名女生
5名女生
6名女生
+ + + =8955(种)
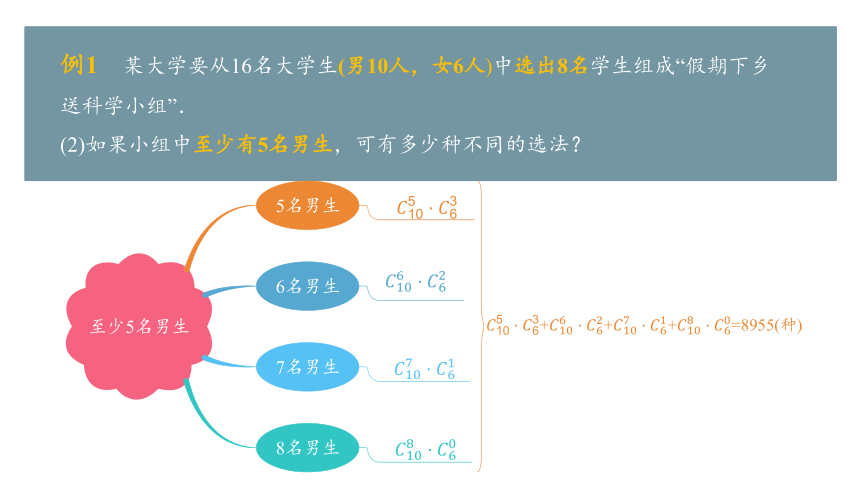
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(2)如果小组中至少有5名男生,可有多少种不同的选法?
至少5名男生
5名男生
6名男生
7名男生
8名男生
+++=8955(种)
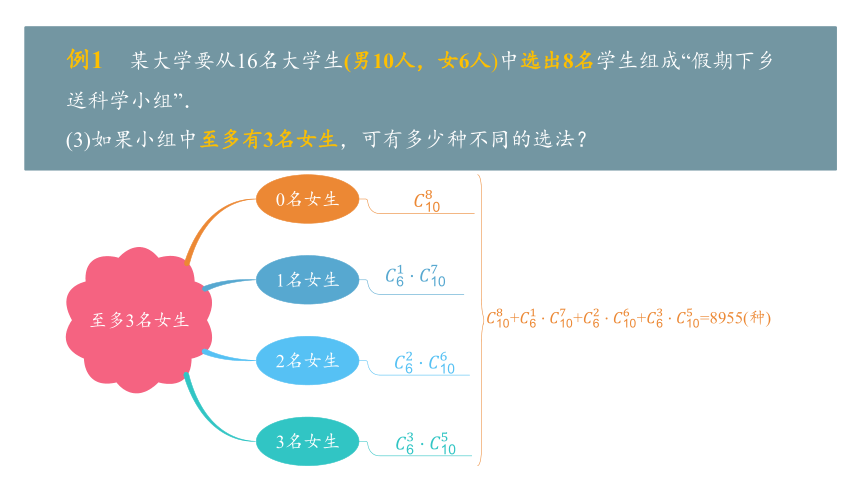
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(3)如果小组中至多有3名女生,可有多少种不同的选法?
至多3名女生
0名女生
1名女生
2名女生
3名女生
+++=8955(种)
特殊元素优先选取
直接法
间接法
正难则反
排除法
类题通法
解答有限制条件
组合问题的
基本方法
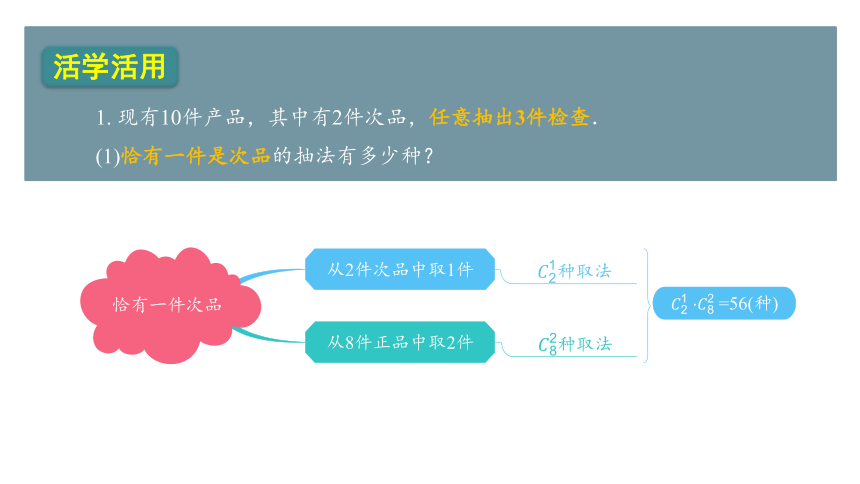
1. 现有10件产品,其中有2件次品,任意抽出3件检查.
(1)恰有一件是次品的抽法有多少种?
从2件次品中取1件
从8件正品中取2件
种取法
种取法
=56(种)
恰有一件次品
活学活用
1. 现有10件产品,其中有2件次品,任意抽出3件检查.
(2)至少有一件是次品的抽法有多少种?
有1件次品
有2件次品
种取法
种取法
+ =64(种)
至少有一件
次品
法一
1、现有10件产品,其中有2件次品,任意抽出3件检查.
(2)至少有一件是次品的抽法有多少种?
10件中任取3件
不含次品
种取法
种取法
- =64(种)
至少有一件
次品
法二
题
型
二
与几何有关的组合问题
例2 平面内有12个点,其中有4个点共线,此外再无任何3点共线.以这些点为顶点,可构成多少个不同的三角形?
典例精析
例2 平面内有12个点,其中有4个点共线,此外再无任何3点共线.以这些点为顶点,可构成多少个不同的三角形?
间接法
12个点中任取3点
共线的4个点中任取3点
种取法
种取法
- =216(个)
选三角形顶点
应掌握处理组合问题的常规方法
要从几何问题中抽象出组合问题
图形多少的问题通常是组合问题
直接法
间接法
解与几何有关
的组合问题
类题通法
2. 四面体的一个顶点为A,从其他顶点和各棱中点中取3个点,
使它们与点A在同一面上,有多少种不同的取法?
如图所示,含顶点A的四面体的3个面上,除点A外每个面都有5个点
从含A的面上取3个点
取含A的棱上的3点与对棱的中点
3 种取法
3种取法
3 =33(种)
活学活用
题
型
三
排列与组合的综合运用
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
典例精析
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
第1类:取出的4张卡片分别标有数字1,2,3,4
第2类:取出的4张卡片分别标有数字1,1,4,4
第3类:取出的4张卡片分别标有数字2,2,3,3
384
24
24
384+24+24=432(种)
取卡片
一般思路:先选后排
是否有序是区分排列组合的基本方法
有限制条件的综合问题
先分析限制条件
然后考虑分类还是分步
解排列、组合
综合问题
注意事项
类题通法
3. 有6名男医生、4名女医生,从中选3名男医生、2名女医生到5个不同的地区巡回医疗,但规定男医生甲不能到地区A,则共有多少种不同的分派方案?
第一类:甲被选中
第二类:甲不被选中
5760+7200=12960(种)
5760
7200
选男女医生
活学活用
1.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有( )
A.140种 B.120种 C.35种 D.34种
选男生女生
1男3女
种
2男2女
种
3男1女
种
+ + =34(种)
D
随堂检测
2.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
A.60种 B.63种 C.65种 D.66种
分3种情况
取4个偶数
=1种
取2奇2偶
=60种
取4个奇数
=5种
1+60+5=66(种)
D
3.7名志愿者中安排6人在周六、周日两天参加社区公益活动,若每天安排3人,则不同的安排方案有________种(用数字作答).
第2步:6人中选3人
=140 (种)
第1步:7人中选6人
140
选志愿者
4.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有________种(用数字作答).
从3个乡镇中任选定
1个乡镇的放法数
任选2名到上一步选定
的乡镇的方法数
剩下的2名大学生分配到
另两个乡镇去的方法数
36
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有1名女生当选;
1名女生,4名男生
×
=350(种)
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(2)两名队长当选;
故共有种选法.
两名队长作为一类,其他11人作为一类
方法
所有选法数量 - 没有队长当选的选法数量
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(3)至少有1名队长当选.
- =825(种)
间接法
6.2.4 组合的应用
高二
选择性必修三
1.进一步理解组合的定义,熟练掌握组合数公式的应用.
2.能解决含有限制条件的组合问题,掌握常见的类型及解决策略.
3.体会简单的排列组合综合问题.
本节目标
考点回顾
排列与组合的
不同点是什么?
利用组合数的性质
应注意什么?
思考总结
题
型
一
组合问题的简单应用
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(1)如果小组中至少有3名女生,可有多少种不同的选法?
(2)如果小组中至少有5名男生,可有多少种不同的选法?
(3)如果小组中至多有3名女生,可有多少种不同的选法?
典例精析
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(1)如果小组中至少有3名女生,可有多少种不同的选法?
至少3名女生
3名女生
4名女生
5名女生
6名女生
+ + + =8955(种)
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(2)如果小组中至少有5名男生,可有多少种不同的选法?
至少5名男生
5名男生
6名男生
7名男生
8名男生
+++=8955(种)
例1 某大学要从16名大学生(男10人,女6人)中选出8名学生组成“假期下乡送科学小组”.
(3)如果小组中至多有3名女生,可有多少种不同的选法?
至多3名女生
0名女生
1名女生
2名女生
3名女生
+++=8955(种)
特殊元素优先选取
直接法
间接法
正难则反
排除法
类题通法
解答有限制条件
组合问题的
基本方法
1. 现有10件产品,其中有2件次品,任意抽出3件检查.
(1)恰有一件是次品的抽法有多少种?
从2件次品中取1件
从8件正品中取2件
种取法
种取法
=56(种)
恰有一件次品
活学活用
1. 现有10件产品,其中有2件次品,任意抽出3件检查.
(2)至少有一件是次品的抽法有多少种?
有1件次品
有2件次品
种取法
种取法
+ =64(种)
至少有一件
次品
法一
1、现有10件产品,其中有2件次品,任意抽出3件检查.
(2)至少有一件是次品的抽法有多少种?
10件中任取3件
不含次品
种取法
种取法
- =64(种)
至少有一件
次品
法二
题
型
二
与几何有关的组合问题
例2 平面内有12个点,其中有4个点共线,此外再无任何3点共线.以这些点为顶点,可构成多少个不同的三角形?
典例精析
例2 平面内有12个点,其中有4个点共线,此外再无任何3点共线.以这些点为顶点,可构成多少个不同的三角形?
间接法
12个点中任取3点
共线的4个点中任取3点
种取法
种取法
- =216(个)
选三角形顶点
应掌握处理组合问题的常规方法
要从几何问题中抽象出组合问题
图形多少的问题通常是组合问题
直接法
间接法
解与几何有关
的组合问题
类题通法
2. 四面体的一个顶点为A,从其他顶点和各棱中点中取3个点,
使它们与点A在同一面上,有多少种不同的取法?
如图所示,含顶点A的四面体的3个面上,除点A外每个面都有5个点
从含A的面上取3个点
取含A的棱上的3点与对棱的中点
3 种取法
3种取法
3 =33(种)
活学活用
题
型
三
排列与组合的综合运用
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
典例精析
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
第1类:取出的4张卡片分别标有数字1,2,3,4
第2类:取出的4张卡片分别标有数字1,1,4,4
第3类:取出的4张卡片分别标有数字2,2,3,3
384
24
24
384+24+24=432(种)
取卡片
一般思路:先选后排
是否有序是区分排列组合的基本方法
有限制条件的综合问题
先分析限制条件
然后考虑分类还是分步
解排列、组合
综合问题
注意事项
类题通法
3. 有6名男医生、4名女医生,从中选3名男医生、2名女医生到5个不同的地区巡回医疗,但规定男医生甲不能到地区A,则共有多少种不同的分派方案?
第一类:甲被选中
第二类:甲不被选中
5760+7200=12960(种)
5760
7200
选男女医生
活学活用
1.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有( )
A.140种 B.120种 C.35种 D.34种
选男生女生
1男3女
种
2男2女
种
3男1女
种
+ + =34(种)
D
随堂检测
2.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
A.60种 B.63种 C.65种 D.66种
分3种情况
取4个偶数
=1种
取2奇2偶
=60种
取4个奇数
=5种
1+60+5=66(种)
D
3.7名志愿者中安排6人在周六、周日两天参加社区公益活动,若每天安排3人,则不同的安排方案有________种(用数字作答).
第2步:6人中选3人
=140 (种)
第1步:7人中选6人
140
选志愿者
4.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有________种(用数字作答).
从3个乡镇中任选定
1个乡镇的放法数
任选2名到上一步选定
的乡镇的方法数
剩下的2名大学生分配到
另两个乡镇去的方法数
36
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有1名女生当选;
1名女生,4名男生
×
=350(种)
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(2)两名队长当选;
故共有种选法.
两名队长作为一类,其他11人作为一类
方法
所有选法数量 - 没有队长当选的选法数量
5.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(3)至少有1名队长当选.
- =825(种)
间接法
