人教版(2019)数学选择性必修三6.3.1二项式定理课件(共30张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三6.3.1二项式定理课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 867.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:40:48 | ||
图片预览







文档简介
(共30张PPT)
6.3.1 二项式定理
高二
选择性必修三
1.能用计数原理证明二项式定理.
2.识记二项式定理及其特征,能用通项公式解决与二项展开式有关的简单问题.
3.通过对二项式定理的研究,体会特殊到一般的规律.
本节目标
提示:(a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
提
出
问
题
问题1:我们在初中学习了(a+b)2=a2+2ab+b2,试用多项式的乘法推导(a+b)3,(a+b)4的展开式.
问题2:上述两个等式的右侧有何特点?
提示:(a+b)3的展开式有4项,每项的次数是3;
(a+b)4的展开式有5项,每一项的次数为4.
新知探究
提
出
问
题
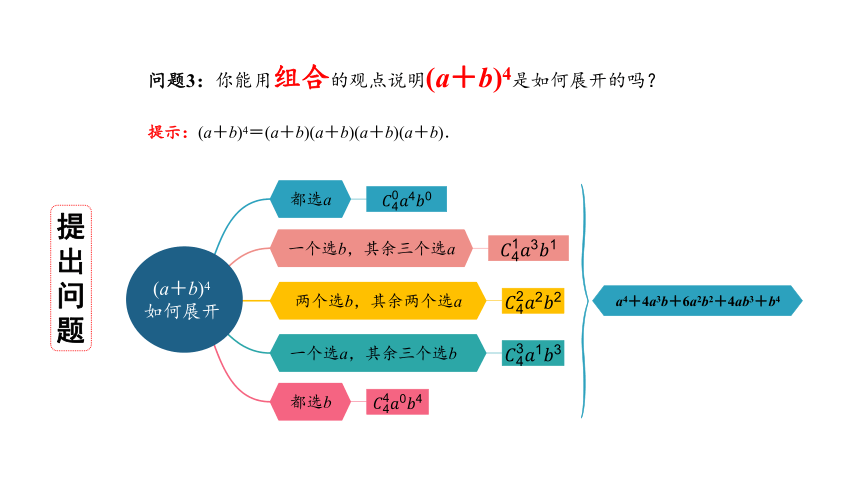
问题3:你能用组合的观点说明(a+b)4是如何展开的吗?
提示:(a+b)4=(a+b)(a+b)(a+b)(a+b).
都选a
一个选b,其余三个选a
两个选b,其余两个选a
一个选a,其余三个选b
都选b
a4+4a3b+6a2b2+4ab3+b4
(a+b)4
如何展开
提
出
问
题
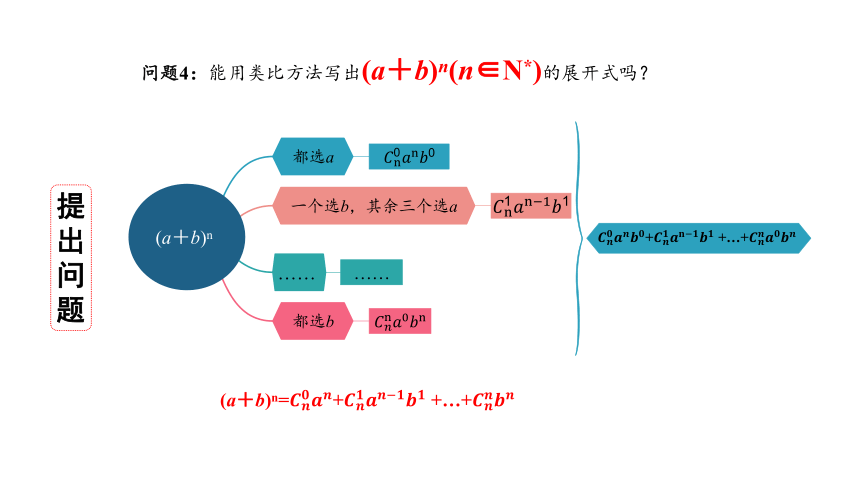
问题4:能用类比方法写出(a+b)n(n∈N*)的展开式吗?
……
都选a
一个选b,其余三个选a
……
都选b
(a+b)n
+ +…+
(a+b)n=+ +…+
导
入
新
知
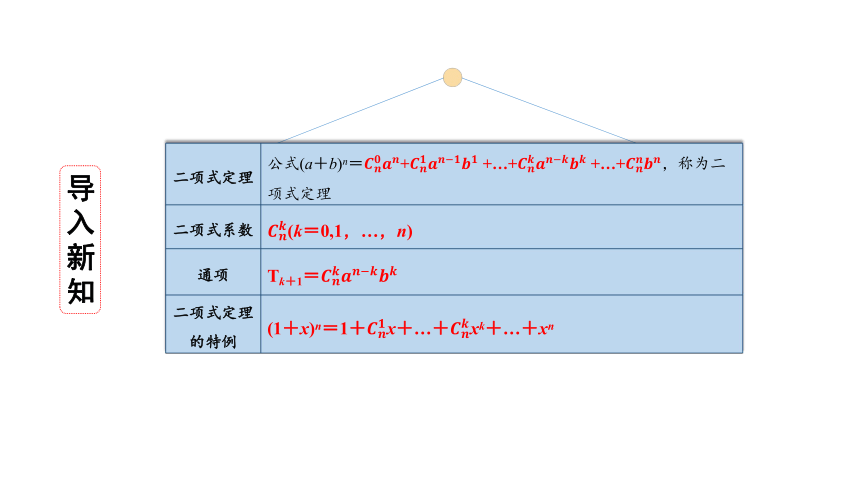
二项式定理 公式(a+b)n=+ +…+ +…+,称为二项式定理
二项式系数 (k=0,1,…,n)
通项 Tk+1=
二项式定理的特例 (1+x)n=1+x+…+xk+…+xn
化解疑难
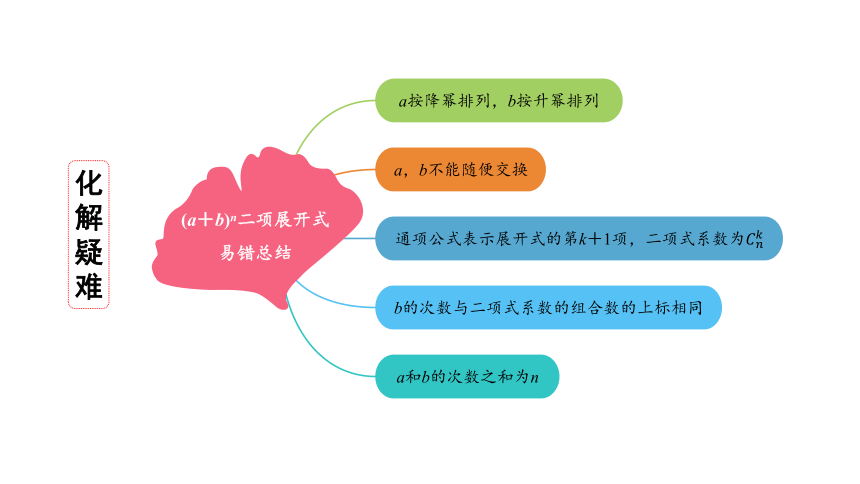
a,b不能随便交换
通项公式表示展开式的第k+1项,二项式系数为
b的次数与二项式系数的组合数的上标相同
a按降幂排列,b按升幂排列
a和b的次数之和为n
(a+b)n二项展开式
易错总结
题
型
一
二项式定理的正用
逆用
例1 (1)求(x+2y)4的展开式.
(2)化简:(x+1)n-(x+1)n-1+(x+1)n-2-…+(-1)k(x+1)n-k+…+(-1)n.
典例精析
例1 (1)求(x+2y)4的展开式.
(x+2y)4=x4+x3(2y)+x2(2y)2+
x(2y)3+(2y)4
=x4+8x3y+24x2y2+32xy3+16y4.
公式正用
例1 (2)化简:(x+1)n-(x+1)n-1+(x+1)n-2-…+(-1)k(x+1)n-k+…+(-1)n.
公式逆用
原式=(x+1)n+(x+1)n-1(-1)+(x+1)n-2(-1)2+…+(x+1)n-k(-1)k+…+(-1)n
=[(x+1)+(-1)]n
=xn.
注意分析多项式的特点,向二项展开式的形式靠拢
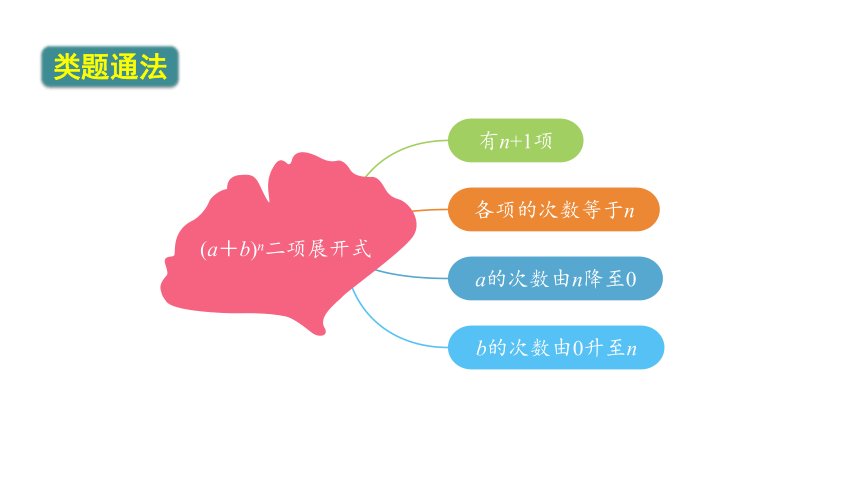
各项的次数等于n
a的次数由n降至0
b的次数由0升至n
有n+1项
类题通法
(a+b)n二项展开式
(1)求的展开式.
直接套公式
法一
活学活用
=(16x4-32x3+24x2-8x+1)
先化简,再套公式
(1)求的展开式.
活学活用
法二
(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
原式=(x-1)5+(x-1)4+(x-1)3+(x-1)2+(x-1)+-
=[(x-1)+1]5-1
=x5-1.
题
型
二
求二项展开式中的特定项
例2 (1)在的展开式中,系数是有理数的项共有( )
A.4项 B.5项 C.6项 D.7项
(2)设二项式的展开式中常数项为A,则A=________.
典例精析
例2 (1)在的展开式中,系数是有理数的项共有( )
A.4项 B.5项 C.6项 D.7项
系数为有理数
与为有理数
k能被2整除,且20-k能被3整除
k=2,8,14,20
A
0≤k≤20
例2 (2)设二项式的展开式中常数项为A,则A=_______.
令=0,得k=3,
所以A=-=-10.
-10
解题策略总结
常数项隐含条件是字母指数为0
有理项一般未知数指数是整数的项
通项公式中的5个量,知4个便可求第5个
类题通法
已知在的展开式中,第6项为常数项.
(1)求n;
通项公式
k=5时,有=0
n=10
活学活用
已知在的展开式中,第6项为常数项.
(2)求展开式中所有的有理项.
通项公式
令=r(r∈Z),则10-2k=3r,即k=5-r.
∵k∈Z,∴r应为偶数.
于是r可取2,0,-2,即k可取2,5,8.
故第3项,第6项与第9项为有理项,它们分别为
(-3)2x2,(-3)5,(-3)8x-2.
题
型
三
求二项式系数与项的系数
例3 在的展开式中,求:
(1)第5项的二项式系数及第5项的系数;
(2)倒数第3项.
典例精析
例3 在的展开式中,求:(1)第5项的二项式系数及第5项的系数;
(2)倒数第3项.
(1) T5=·(2x2)8-4·= ·24·,
第5项的二项式系数是=70,
第5项的系数是·24=1120.
(2) 展开式中的倒数第3项即为第7项,
T7= ·(2x2)8-6· =112x2.
利用通项公式求解
方法技巧
总结
展开式的倒数第3项就是展开式的第3项
注意区分二项式系数与指定某一项的系数
类题通法
(1)若展开式的常数项为60,则常数a的值为________.
令6-3k=0
k=2
常数项是a
常数项为60
a=60
a=4
4
活学活用
(2) (四川高考)二项式(x+y)5的展开式中,含x2y3的项的系数是________(用数字作答).
含x2y3的项
k=3
T4=x2y3=10x2y3
10
D
1.在(x-)10的展开式中,含x6的项的系数是( )
A.-27 B.27
C.-9 D.9
随堂检测
2.在的展开式中常数项是( )
A.-28 B.-7 C.7 D.28
当=0,即k=6时,T7=(-1)6·=7.
C
3.在的展开式中,中间项是________.
n=6
中间项是第4项
=·(-1)3·23·x3
T4=-160x3
-160x3
4. 的展开式中,第4项的二项式系数是______,第4项的系数是________.
第4项的二项式系数为=84,项的系数为
84
5.求的展开式的第三项的系数和常数项.
第三项的系数为 =
令15-5k=0得k=3
常数项为
6.3.1 二项式定理
高二
选择性必修三
1.能用计数原理证明二项式定理.
2.识记二项式定理及其特征,能用通项公式解决与二项展开式有关的简单问题.
3.通过对二项式定理的研究,体会特殊到一般的规律.
本节目标
提示:(a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
提
出
问
题
问题1:我们在初中学习了(a+b)2=a2+2ab+b2,试用多项式的乘法推导(a+b)3,(a+b)4的展开式.
问题2:上述两个等式的右侧有何特点?
提示:(a+b)3的展开式有4项,每项的次数是3;
(a+b)4的展开式有5项,每一项的次数为4.
新知探究
提
出
问
题
问题3:你能用组合的观点说明(a+b)4是如何展开的吗?
提示:(a+b)4=(a+b)(a+b)(a+b)(a+b).
都选a
一个选b,其余三个选a
两个选b,其余两个选a
一个选a,其余三个选b
都选b
a4+4a3b+6a2b2+4ab3+b4
(a+b)4
如何展开
提
出
问
题
问题4:能用类比方法写出(a+b)n(n∈N*)的展开式吗?
……
都选a
一个选b,其余三个选a
……
都选b
(a+b)n
+ +…+
(a+b)n=+ +…+
导
入
新
知
二项式定理 公式(a+b)n=+ +…+ +…+,称为二项式定理
二项式系数 (k=0,1,…,n)
通项 Tk+1=
二项式定理的特例 (1+x)n=1+x+…+xk+…+xn
化解疑难
a,b不能随便交换
通项公式表示展开式的第k+1项,二项式系数为
b的次数与二项式系数的组合数的上标相同
a按降幂排列,b按升幂排列
a和b的次数之和为n
(a+b)n二项展开式
易错总结
题
型
一
二项式定理的正用
逆用
例1 (1)求(x+2y)4的展开式.
(2)化简:(x+1)n-(x+1)n-1+(x+1)n-2-…+(-1)k(x+1)n-k+…+(-1)n.
典例精析
例1 (1)求(x+2y)4的展开式.
(x+2y)4=x4+x3(2y)+x2(2y)2+
x(2y)3+(2y)4
=x4+8x3y+24x2y2+32xy3+16y4.
公式正用
例1 (2)化简:(x+1)n-(x+1)n-1+(x+1)n-2-…+(-1)k(x+1)n-k+…+(-1)n.
公式逆用
原式=(x+1)n+(x+1)n-1(-1)+(x+1)n-2(-1)2+…+(x+1)n-k(-1)k+…+(-1)n
=[(x+1)+(-1)]n
=xn.
注意分析多项式的特点,向二项展开式的形式靠拢
各项的次数等于n
a的次数由n降至0
b的次数由0升至n
有n+1项
类题通法
(a+b)n二项展开式
(1)求的展开式.
直接套公式
法一
活学活用
=(16x4-32x3+24x2-8x+1)
先化简,再套公式
(1)求的展开式.
活学活用
法二
(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
原式=(x-1)5+(x-1)4+(x-1)3+(x-1)2+(x-1)+-
=[(x-1)+1]5-1
=x5-1.
题
型
二
求二项展开式中的特定项
例2 (1)在的展开式中,系数是有理数的项共有( )
A.4项 B.5项 C.6项 D.7项
(2)设二项式的展开式中常数项为A,则A=________.
典例精析
例2 (1)在的展开式中,系数是有理数的项共有( )
A.4项 B.5项 C.6项 D.7项
系数为有理数
与为有理数
k能被2整除,且20-k能被3整除
k=2,8,14,20
A
0≤k≤20
例2 (2)设二项式的展开式中常数项为A,则A=_______.
令=0,得k=3,
所以A=-=-10.
-10
解题策略总结
常数项隐含条件是字母指数为0
有理项一般未知数指数是整数的项
通项公式中的5个量,知4个便可求第5个
类题通法
已知在的展开式中,第6项为常数项.
(1)求n;
通项公式
k=5时,有=0
n=10
活学活用
已知在的展开式中,第6项为常数项.
(2)求展开式中所有的有理项.
通项公式
令=r(r∈Z),则10-2k=3r,即k=5-r.
∵k∈Z,∴r应为偶数.
于是r可取2,0,-2,即k可取2,5,8.
故第3项,第6项与第9项为有理项,它们分别为
(-3)2x2,(-3)5,(-3)8x-2.
题
型
三
求二项式系数与项的系数
例3 在的展开式中,求:
(1)第5项的二项式系数及第5项的系数;
(2)倒数第3项.
典例精析
例3 在的展开式中,求:(1)第5项的二项式系数及第5项的系数;
(2)倒数第3项.
(1) T5=·(2x2)8-4·= ·24·,
第5项的二项式系数是=70,
第5项的系数是·24=1120.
(2) 展开式中的倒数第3项即为第7项,
T7= ·(2x2)8-6· =112x2.
利用通项公式求解
方法技巧
总结
展开式的倒数第3项就是展开式的第3项
注意区分二项式系数与指定某一项的系数
类题通法
(1)若展开式的常数项为60,则常数a的值为________.
令6-3k=0
k=2
常数项是a
常数项为60
a=60
a=4
4
活学活用
(2) (四川高考)二项式(x+y)5的展开式中,含x2y3的项的系数是________(用数字作答).
含x2y3的项
k=3
T4=x2y3=10x2y3
10
D
1.在(x-)10的展开式中,含x6的项的系数是( )
A.-27 B.27
C.-9 D.9
随堂检测
2.在的展开式中常数项是( )
A.-28 B.-7 C.7 D.28
当=0,即k=6时,T7=(-1)6·=7.
C
3.在的展开式中,中间项是________.
n=6
中间项是第4项
=·(-1)3·23·x3
T4=-160x3
-160x3
4. 的展开式中,第4项的二项式系数是______,第4项的系数是________.
第4项的二项式系数为=84,项的系数为
84
5.求的展开式的第三项的系数和常数项.
第三项的系数为 =
令15-5k=0得k=3
常数项为
